Faraz Arbabi, Ph.D.
Data Scientist at Gnowise Inc., Toronto, Ontario, Canada
faraz@gnowise.com
Finite element, finite difference, and finite volume methods are among the most popular methods for solving partial differential equations governing many problems in engineering and material sciences. Calculating stress distribution in physical systems requires extensive computational resources through implementing software packages, and can take hours, days or weeks to execute for complex geometries. More importantly, the simulation need to be redone from scratch to apply new boundary conditions or material properties during the design process. These drawbacks of conventional stress analysis methods limit opportunities for interactive design. Recent advances in deep learning algorithms demonstrate that by approperiate selection of models and at a cost of minor additional computational errors we can significantly accelerate the stress analysis methods. In this note, I discuss the feasibility of complementing finite volume method with deep learning through providing a case study. The outcomes show that using Convolutional Neural Network method, we can reduce the computational time by 82%, while obtaining the results with 94.2% accuracy.
Recent studies have shown the possibility of incorporating machine learning (ML) and deep learning methods to obtain faster and less costly solutions for stress analysis problems. Nguyen-Thien and Tran-Cong [1] showed the capability of Artificial Neural Network (ANN) methods in implementing numerical approximation of functions of several variables and their first and second order partial derivatives. Martin-Guerrerohas et al. [2] demonstrated the feasibility of using ANN to model the deformations produced in human soft tissue with high accuracy. They used finite element method (FEM) to produce the datasets of deformation to feed the ML algorithm. Kononenko and Kononenko [3] as well as Javadi et al. [4] integrated neural networks with finite element method to analyse stress distribution simple one dimensional (1D) problems. These studies either used a small dataset for training their model, or provided simple 1D problems as test cases. In this study I show the feasibility of using neural networks for faciliating stress analysis problems on more complex, two dimensional (2D) problems. Here, I use finite volume method (FVM) to calculate the stress distribution on a 2 plate with a circular hole for various forces applied. I use the generated dataset of results to train a Convolutional Neural Netwrok (CNN) model and predict stress distribution over the plate for uncalculated forces. The results will be compared to the test data to calculate the accuracy of the model.
The 2D flat plate with hole that I use in this study as test case is illustrated in Figure 1. The simulations were done on a quarter of the plate, as the problem is symmetric. The forces were applied on the right and left edges. The grid was generated non-uniformly with finer numerical cells closer to the boundaries, forming a total of 1071 numerical cells.
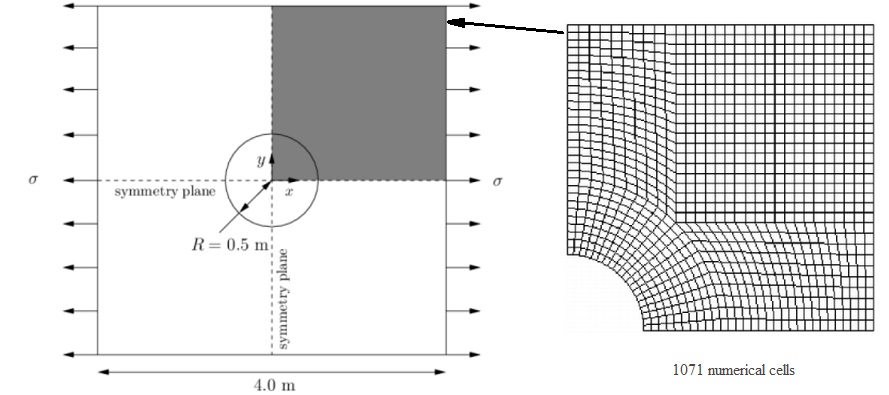
Fig.1. Schematic illustration of the geometry.
The numerical simulations were conducted using OpenFOAM 2.3 software package. The FVM method was employed for calculating partial differential equations. Each simulation took around 0.14 seconds on Intel Core-i7, 3.4GHz, 16Gb RAM. The stress distribution as a result of applied stress of 1000Pa is shown in Figure 2.
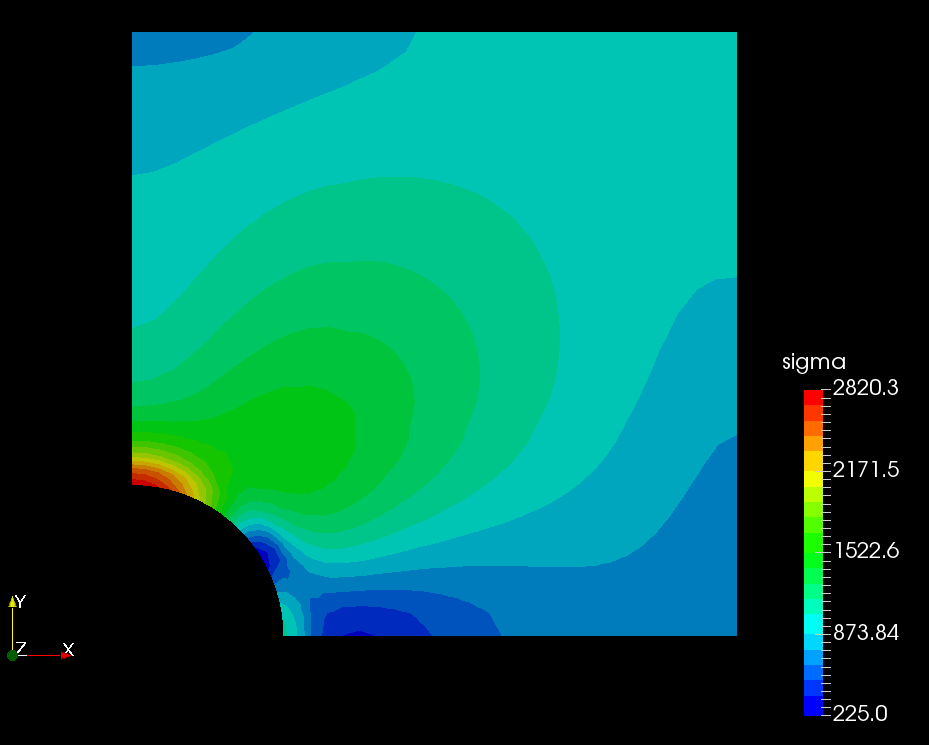
Fig.2. A sample of the simulation results (S=1000Pa).
To create the database of training and score data, a series of simulations were conducted on a range of applied stresses (i.e. 0, 1000, 2000, … 100,000(Pa)) resulting in 101 dataset (each 1071 rows). The train dataset includes the coordinates of each grid point, the applied stress, and the stress values calculated using FVM (see Figure 3).

Fig.3. Training, test and score datasets.
A four layer CNN model was created using Keras library in Python 3.6, and Sigmond function was used as the activation function.
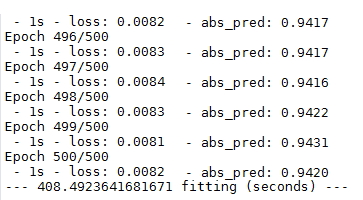
After compilation, the model was trained using 90% of the data as the train data for 500 epochs. I was able to obtain an accuracy of 94.2% (see Figure 4).
In order to evaluate the speed of the model, I regenerated the sample result for S=1000Pa (see Figure 5).
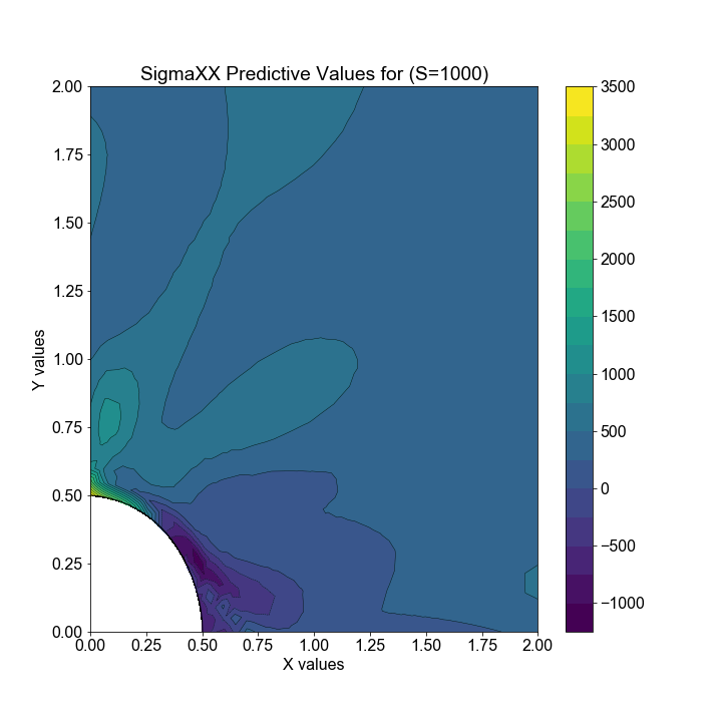
Fig.5. CNN model output for S=1000Pa.
The CNN model returned the results in around 0.012 seconds, which is 82% faster compared to the FVM method on the same computer (see Figure 6).
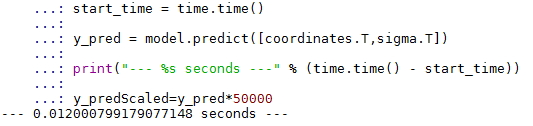
Fig.6. CNN model execution time.
This work showed the feasibility of CNN method for solving 2D stress analysis problems significantly faster than the conventional FEM, FDM, and FVM methods at a cost of low additional errors. It should be noted that this project is still under development, and I believe it is possible to reduce the CNN error by adding more hidden layers, optimizing the hyperparameters, and increasing the size of training dataset.
[1] Nguyen-Thien, T. & Tran-Cong, T. Approximation of functions and their derivatives: A neural network implementation with applications. Applied Mathematical Modelling 23, 687-704, doi:https://doi.org/10.1016/S0307-904X(99)00006-2 (1999).
[2] Martín-Guerrero, J. D. et al. in Data Mining Workshops (ICDMW), 2016 IEEE 16th International Conference on. 247-253 (IEEE).
[3] Kononenko, O. & Kononenko, I. Machine Learning and Finite Element Method for Physical Systems Modeling. arXiv preprint arXiv:1801.07337 (2018).
[4] Javadi, A., Tan, T. & Zhang, M. Neural network for constitutive modelling in finite element analysis. Computer Assisted Mechanics and Engineering Sciences 10, 523-530 (2003).