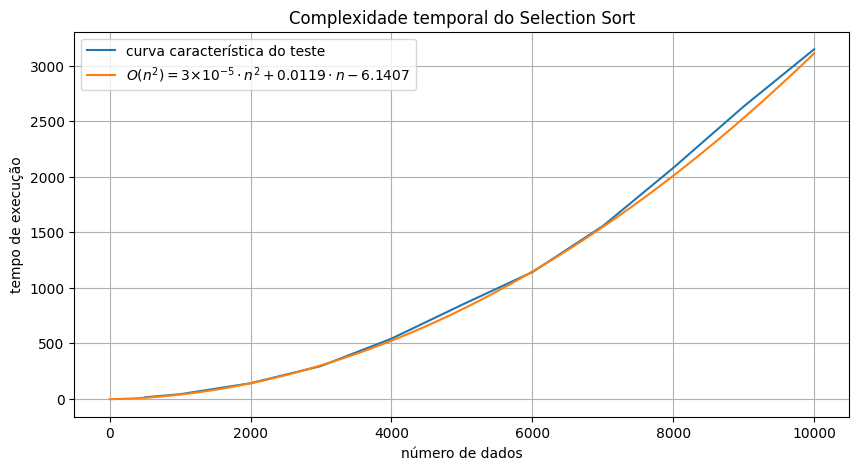
O projeto de ordenação de strings emprega o algoritmo Selection Sort por meio da linguagem C. O Selection Sort é um método algorítimico que consiste em posicionar iterativamente o menor valor do conjunto em análise na primeira posição do vetor, em seguida, o segundo menor valor é colocado na segunda posição, e esse procedimento é reiterado de forma sequencial. A direção da ordenação pode ser ajustada para ser crescente ou decrescente, de acordo com a intenção do usuário. No presente contexto, a ordenação das strings é realizada na sequência que vai do valor mais baixo ao mais alto.
void func_ordena(Funcionario **func, int count)
{
int i, primeiroID, j;
Funcionario *valor_teste;
for (i = 0; i < count; i++)
{
valor_teste = func[i];
primeiroID = i;
for (j = i + 1; j < count; j++)
{
if (func_compara(func[primeiroID]->nome, func[j]->nome) == 1)
{
primeiroID = j;
}
}
if (primeiroID != i)
{
func[i] = func[primeiroID];
func[primeiroID] = valor_teste;
}
}
}A complexidade de espaço de um algoritmo, S(P), é a análise do espaço de memória requerido para a sua execução, que consiste tanto a parte fixa quanto a parte variável do espaço.
No Selection Sort, a parte fixa consiste nas quatro variáveis do tipo int, que ocupam 4 Bytes de memória cada, e o ponteiro para a struct Funcionario, que possui 8 Bytes, considerando o tamanho de todos os parâmetros juntos. Totalizando 24 Bytes fixos.
E a parte variável, consiste no vetor de ponteiros para a struct Funcionario, que irá ocupar o equivalente a (n*8) Bytes, sendo n o número de entrada da variável int count.
Dessa forma, o Selection Sort possui complexidade espacial de
A complexidade de tempo de um algoritmo, T(n), é a análise do tempo de execução do mesmo. O Selection Sort possui complexidade
void func_ordena(Funcionario **func, int count)
{
int i, primeiroID, j; // c1
Funcionario *valor_teste; // c2
for (i = 0; i < count; i++) // c3*n
{
valor_teste = func[i]; // c4*n
primeiroID = i; // c5*n
for (j = i + 1; j < count; j++) //c6*n*(n-1)/2
{
if (func_compara(func[primeiroID]->nome, func[j]->nome) == 1) // c7*n*(n-1)/2
{
primeiroID = j; // c8*n*(n-1)/2
}
}
if (primeiroID != i) // c9*n
{
func[i] = func[primeiroID]; // c10*n
func[primeiroID] = valor_teste; // c11*n
}
}
}Os termos constantes foram nomeados como a, b os termos que acompanham (n) e c os termos que acompanham [n*(n-1)/2]