In pure Python.
This project provides a pure Python code for searching sub-optimal solutions to the TSP. Additionally, demonstration scripts for visualization of results are provided.
The library does not requires any libraries, but demo scripts require:
- Numpy
- PIL (Python imaging library)
- Matplotlib
- tsp_solver.greedy : Basic greedy TSP solver in Python
- tsp_solver.greedy_numpy : Version that uses Numpy matrices, which reduces memory use, but performance is several percents lower
- tsp_solver.demo : Code for the demo applicaiton
- demo_tsp : Generates random TSP, solves it and visualises the result. Optionally, result can be saved to the numpy-format file.
- tsp_numpy2svg : Generates neat SVG image from the numpy file, generated by the demo_tsp.
Both applications support a variety of command-line keys, run them with --help option to see additional info.
Install from PyPi:
# pip install tsp_solver2or
$ pip install --user tsp_solver2(Note taht tsp_solver package contains an older version).
Manual installation:
# python setup.py installAlternatively, you may simply copy the tsp_solver/greedy.py to your project.
The library provides a greedy solver for the symmetric TSP. Basic usage is:
from tsp_solver.greedy import solve_tsp
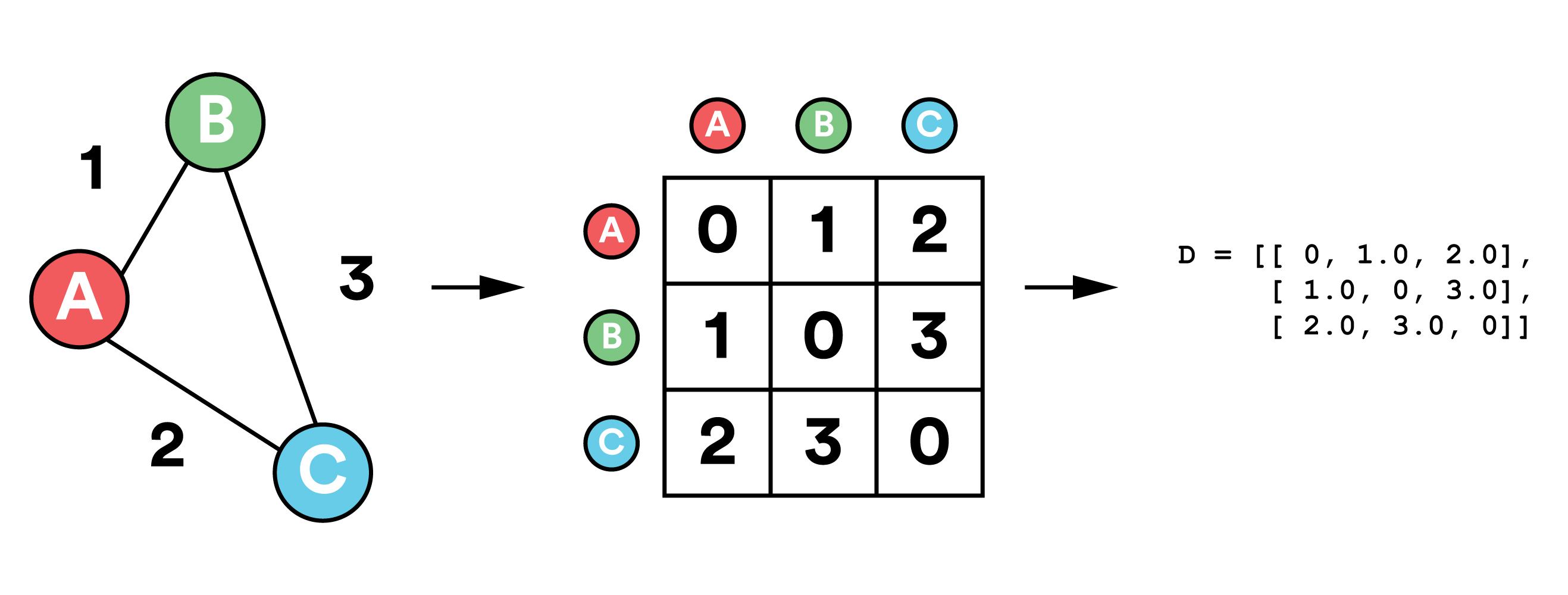
#Prepare the square symmetric distance matrix for 3 nodes:
# Distance from A to B is 1.0
# B to C is 3.0
# A to C is 2.0
D = [[],
[1.0],
[2.0, 3.0]]
path = solve_tsp( D )
#will print [1,0,2], path with total length of 3.0 units
print(path)The triangular matrix D in the above example represents the following graph with three nodes A, B, and C:
Square matrix may be provided, but only left triangular part is used from it.
The library implements a simple "greedy" algorithm:
- Initially, each vertex belongs to its own path fragment. Each path fragment has length 1.
- Find 2 nearest disconnected path fragments and connect them.
- Repeat, until there are at least 2 path fragments.
This algorightm has polynomial complexity.
Greedy algorithm sometimes produces highly non-optimal solutions. To solve this, optimization is provided. It tries to rearrange points in the paths to improve the solution. One optimization pass has O(n^4) complexity. Note that even unlimited number of optimization paths does not guarantees to find the optimal solution.
This library neither implements a state-of-the-art algorithm, nor it is tuned for a high performance.
It however can find a decent suboptimal solution for the TSP with 4000 points in several minutes. The biggest practical limitation is memory: O(n^2) memory is used.
To see a demonstration, run
$ make demowithout installation. The demo requires Numpy and Matplotlib python libraries to be installed.
To execute unit tests, run
$ make test