El objetivo de este proyecto es resolver el problema Titanic - Machine Learning from Disaster de Kaggle Competition utilizando algoritmos de clasificación. Para ello, se seguirán las siguientes etapas:
- Verificar si los datos están balanceados en las clases en las cuales se deben separar los datos.
Para el conjunto de datos del reto Titanic nuestra tarea es predecir si un pasajero sobrevivió o no al naufragio. Es decir, las clases objetivo son "sobrevivió" y "no sobrevivió".
Hemos considerado que los datos NO están equilibrados ya que el número de muestras de pasajeros que sobrevivieron es mayor al número de muestras de pasajeros que no sobrevivieron. El porcentage qué 'sobrevivió' [549 personas] es: 61.62 %. El porcentage of 'no sobrevivió' [341 personas] es 38.38%.
Está verificación del equilibrio de clases es importante para nuestro análisis de datos y la modelización, ya que un desequilibrio significativo puede llevar a problemas de sesgo en los modelos de machine learning. Si una clase está sobrerepresentada en comparación con la otra, el modelo puede tener dificultades para aprender y predecir la clase minoritaria de manera efectiva. Por lo tanto, fue fundamental evaluar y abordar el desequilibrio de clases en el preprocesamiento de datos antes de entrenar cualquier modelo.
- Analizar la distribución de los datos categóricos y su relación con la clase "survived". Comienza a identificar características relevantes para una clasificación precisa.
Los atributos categóricos son:
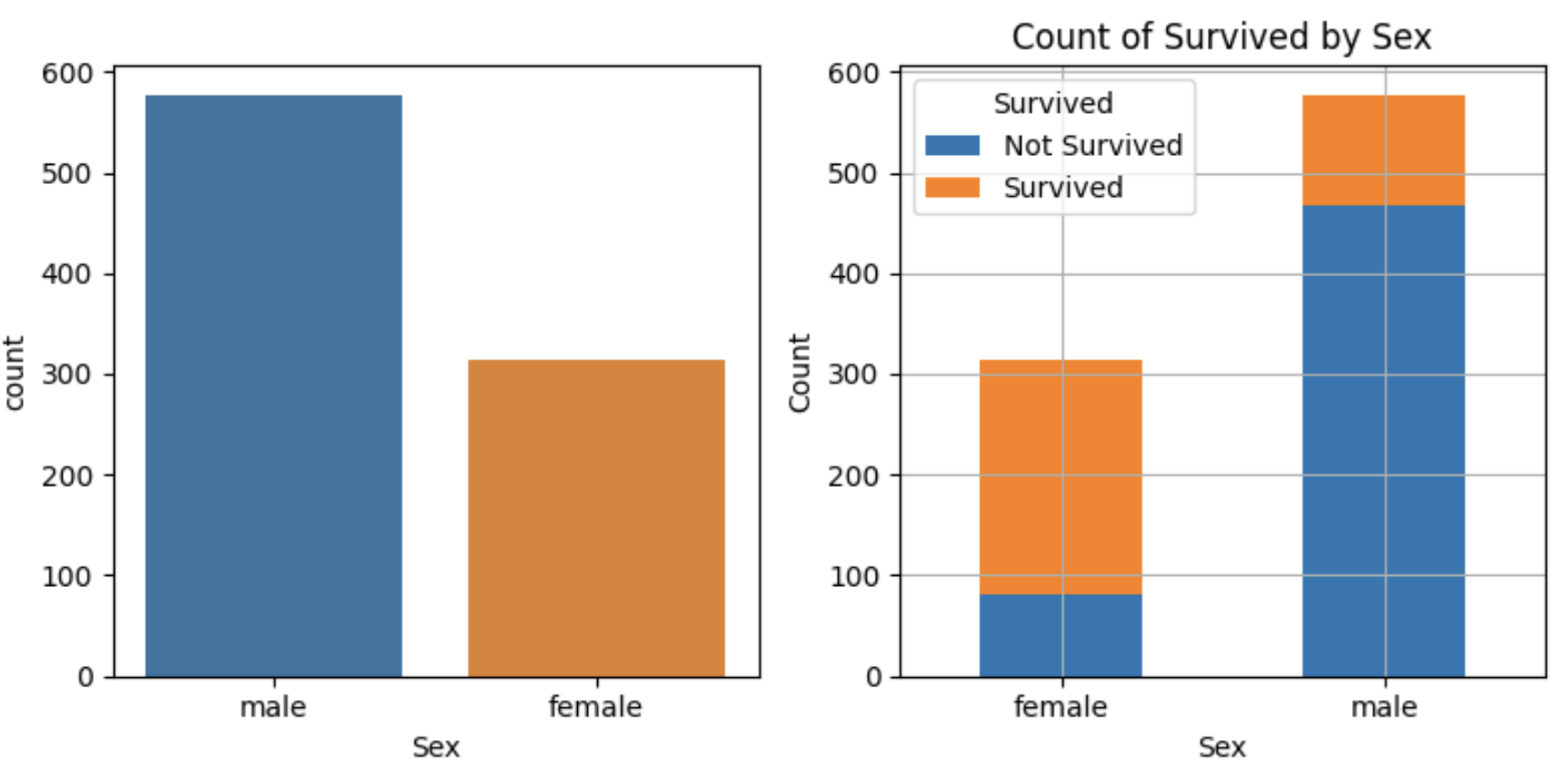
Porcentage of male ( 577 ): 64.76 %
Porcentage of female ( 314 ): 35.24 %
Porcentage of male surviving: 18.89 %
Porcentage of male not surviving: 81.11 %
Porcentage of female surviving: 74.2 %
Porcentage of female not surviving: 25.8 %
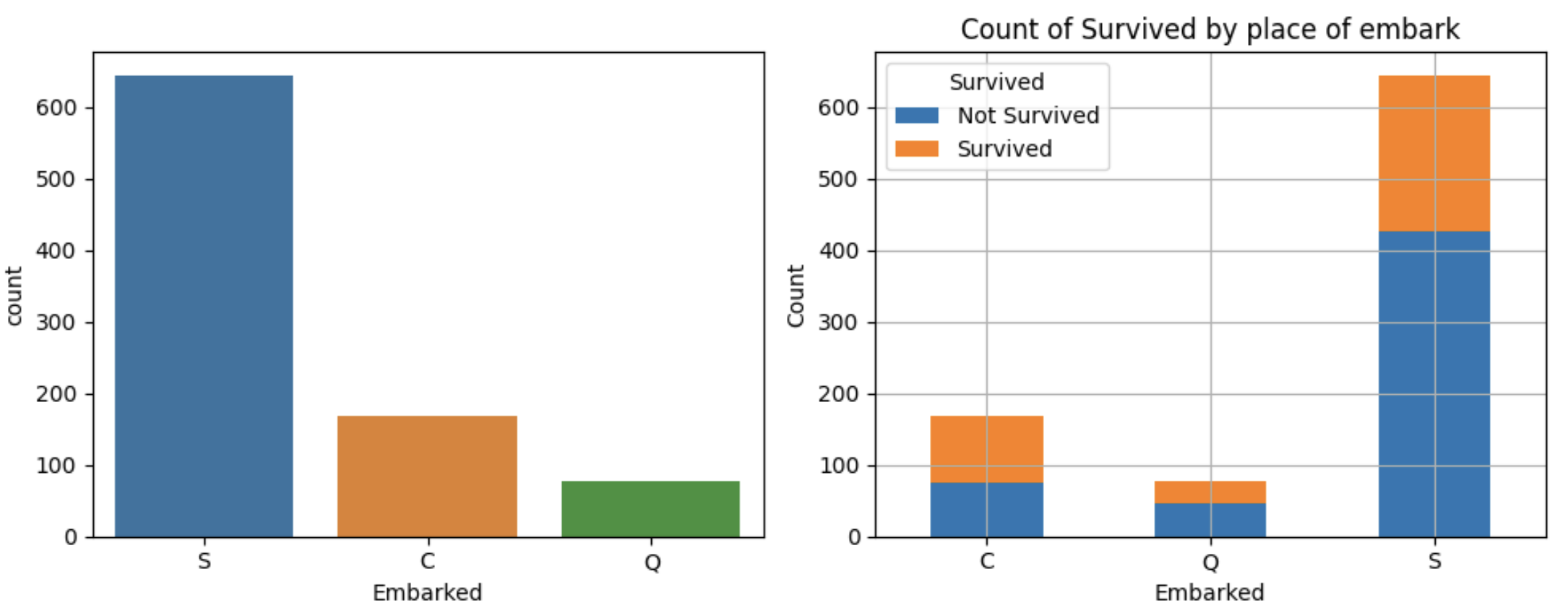
Porcentage of embark in C = Cherbourg ( 168 ): 18.86 % Not-Survived: 44.64 % Survived: 55.36 %
Porcentage of embark in Q = Queenstown ( 77 ): 8.64 % Not-Survived: 61.04 % Survived: 38.96 %
Porcentage of embark in S = Southampton ( 644 ): 72.28 % Not-Survived: 66.3 % Survived: 33.7 %
Hemos decidido no utilizar los atributos 'Name', 'Ticket' y 'Cabin'. Creemos que no aportan una mejora significativa en nuestras predicciones. De hecho, probamos extraer los prefijos Mr, Miss, Don, Lady, para analizar si había alguna relación con 'sobrevivir' o 'no sobrevivir' pero nos dimos cuenta que dichos prefijos están estrechamente ligados al 'sexo' de una persona. Es decir, aquellos que tienen prefijos masculinos son hombres y viceversa.
- Comprender la distribución de los datos numéricos y determinar si es necesario aplicar procesos de normalización o estandarización.
Los atributos númericos son:
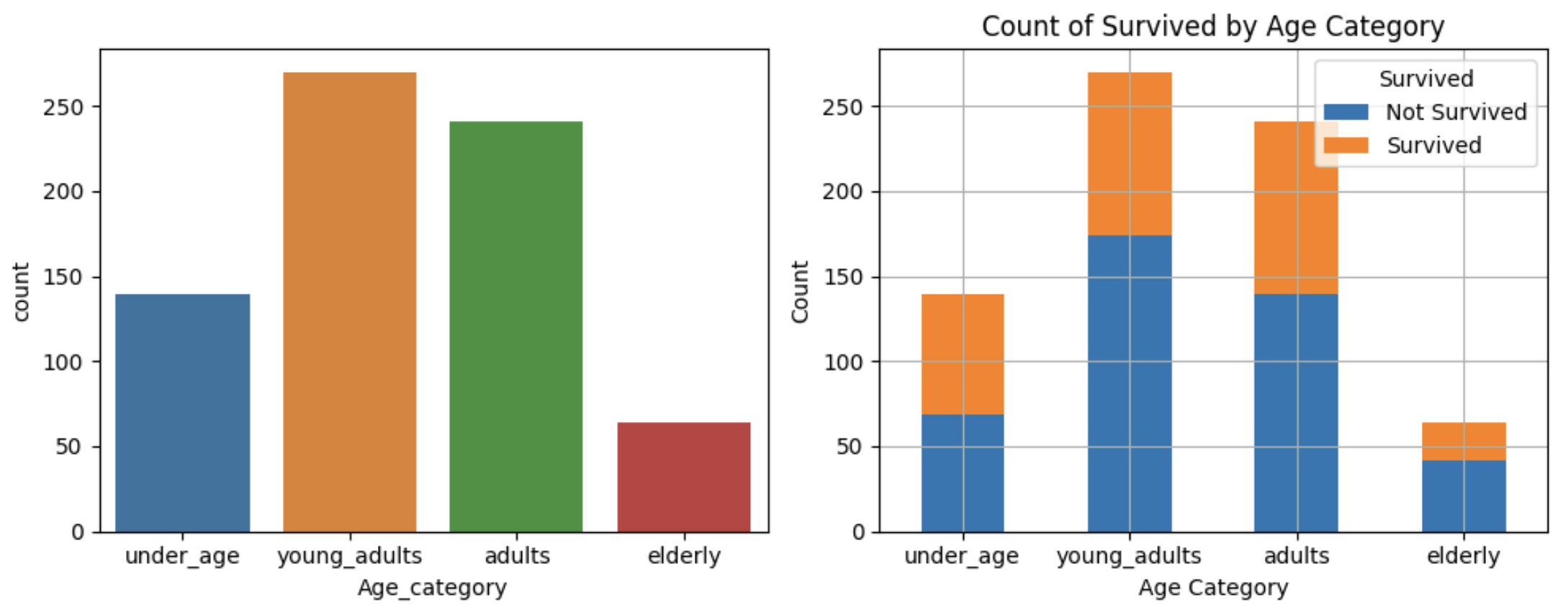
Young adults ( 270 ): 19 - 30 years old Not-Survived: 64.44 % Survived: 35.56 %
Adults ( 241 ): 30 - 50 years old Not-Survived: 57.68 % Survived: 42.32 %
Elderly ( 64 ): 50+ years old Not-Survived: 65.62 % Survived: 34.38 %
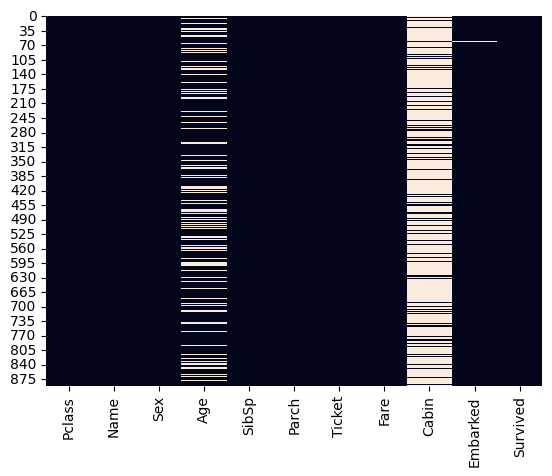
- Identificar y visualizar los datos faltantes.
Pclass has 0 missing values
Name has 0 missing values
Sex has 0 missing values
Age has 177 missing values
SibSp has 0 missing values
Parch has 0 missing values
Ticket has 0 missing values
Fare has 0 missing values
Cabin has 687 missing values
Embarked has 2 missing values
Survived has 0 missing values
- Decidir qué características requieren imputaciones y cuáles no. Justificar la decisión y eliminar las columnas no seleccionadas.
La decisión de qué características requieren imputaciones la tomamos bajo los siguientes criterios:
-
Age: Tiene 177 valores faltantes. Dado que la edad podría ser una característica importante para predecir la supervivencia en el contexto del Titanic (por ejemplo, es probable que los niños tengan tasas de supervivencia diferentes a los adultos), creímos razonable imputar estos valores faltantes.
-
Cabin: Tiene 687 valores faltantes. Dado que la cantidad de valores faltantes es considerablemente alta, hemos decidido eliminar esta característica en su totalidad. Además, creemos que la información de la cabina puede no ser esencial para predecir la supervivencia.
-
Embarked: Tiene 2 valores faltantes. Dado que solo hay dos valores faltantes, decidimos imputarlos utilizando la moda (el valor más común) de la característica "Embarked".
- Aplicar técnicas de imputación para los datos faltantes. Seleccionar la mejor técnica y justificar la elección.
Usamos la técnica incluída en scikit learn para realizar imputaciones.
from sklearn.impute import SimpleImputer
Para los valores numéricos usamos:
imputer_num = SimpleImputer(strategy="median")
Para los valores categóricos usamos:
"imputer_cat = SimpleImputer(strategy="most_frequent")
Usamos la mediana porque es una medida de tendencia central robusta que no se ve afectada por valores extremos o atípicos. En el caso de "Age", podría haber valores atípicos que afecten la media, es por eso que la mediana fue nuestra elección más robusta para imputar los valores faltantes.
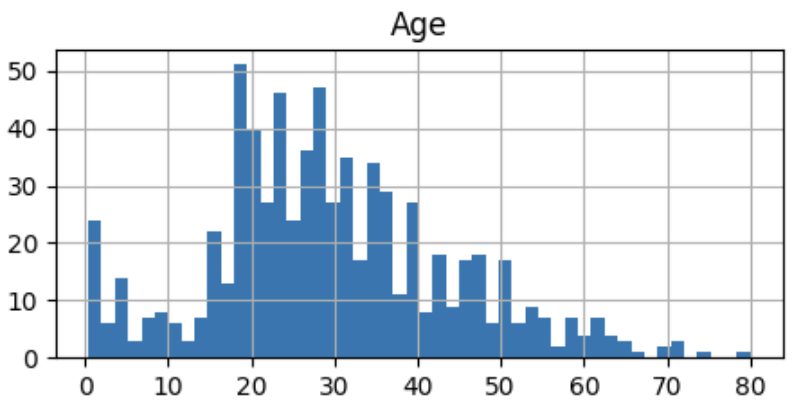
Observamos que la distribución de "Age" es asimétrica pero NO contiene valores atípicos significativos. Aun así, creímos preferible utilizar la mediana para evitar la influencia de estos valores atípicos en la imputación. Además, dicha asimetría no es muy significativa, dado que la desviación estándar es de 14. A continuación presentamos una gráfica que refleja la distribución de esta categoria numérica:
Por otro lado, para la categoría 'Embarked' únicamente imputamos 2 valores. Decidimos usar la estrategia de reemplazo por el valor más frecuente también conocida como la moda, está decisión se tomó para seguir la tendencia central y dar una distribución concisa a la categoría.
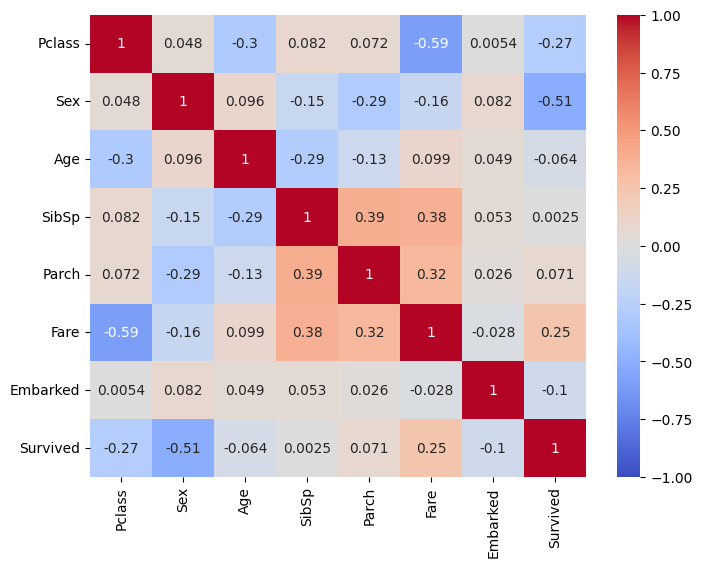
- Realizar un análisis de correlación para decidir qué características deben mantenerse y cuáles descartarse.
El resultado del análisis de correlación dio la siguiente figura:
Con base en esta figura vemos que el rango de valores va de -1 a 1. -1 indica que hay una fuerte correlación negativa. 0 nos indica que no hay correlación. 1 nos indica que hay una fuerte correlación positiva.
-
Survived:
- Su correlación con otros atributos es lógicamente de gran interes:
- Hay correlación positiva con Fare (0.247519).
- Hay correlación negativa con Pclass (-0.268318) y Sex (-0.509660).
- Su correlación con otros atributos es lógicamente de gran interes:
-
Pclass:
- Su correlación con 'Fare' y 'Age' fue como sigue:
- Correlación negativa con Fare (-0.594245).
- Correlación negativa con Age (-0.304298).
- El hecho de que esté correlacionada con otras 2 clases / atributos, nos pareció como un atributo robusto para las predicciones.
- Su correlación con 'Fare' y 'Age' fue como sigue:
-
Sex:
- Tuvo una fuerte correlación negativa con 'Sobrevivió' (-0.509660), asi que la mantuvimos pues creímos que es un predictor significativo.
-
Age:
- Tiene una correlación negativa con Pclass (-0.304298). Decidimos agrupar Age en categorías para mejorar la distribución y asemejarla más a una campana gaussiana. Sin embargo, vemos que su correlación con otros atributos no es tan fuerte como lo hubieramos pensado en un inicio. No es un atributo que tenga gran significado en las predicciones.
-
SibSp:
- Tiene una correlación positiva con Parch (0.392197). Este atributo decidimos combinarlo con Parch para la creación de un nuevo feature llamado 'Travel Alone'. El objetivo fue identificar a los pasajeros que viajaron junto a su familia y aquellos pasajeros que viajaron solitariamente. Creemos que este factor puede ser un buen predictor de supervivencia.
-
Parch:
- Mismo caso que SibSp.
-
Fare:
- Fare es un atributo interesante porque tiene correlaciones negativas fuertes con 'Pclass' (-0.594245) y correlaciones positivas con 'Survived' (0.247519) y moderadamente correlacionada con otros atributos.
-
Embarked:
- No tiene correlaciones fuertes pero decidimos quedarnoslo como una versión de prueba. Sin embargo, también optamos por eliminarlo para probar nuestros modelos en una segunda iteración.
- Convertir los datos categóricos en numéricos. Explorar diferentes métodos y seleccionar el más adecuado. Justificar la elección.
Para la transformación de los datos usamos el siguiente codificador:
from sklearn.preprocessing import OneHotEncoder
onehot = OneHotEncoder(handle_unknown="ignore")
La elección de codificación estuvo entre OneHotEncoder y Codificación por enteros (por ejemplo, [0, 1, 2]) para variables categóricas. Tomamos nuestra decisión basándonos en los modelos que ibamos a usar, concluímos que la mejor estrategia sería usar OneHotEncoder. Además, sabemos que cuando aplicamos una transformación, la regla que podemos usar cuando no hay ningún parámetro confiable en qué basarnos, es hacer una transformación de One-Hot en vez de Codificación por enteros.
1. Regresión Logística:
- Elección de Codificación: Usualmente, la codificación one-hot es una mejor opción para la regresión logística. Esto se debe a que la regresión logística no asume ninguna relación ordinal inherente entre las categorías, y la codificación one-hot garantiza que cada categoría se trate como una característica binaria separada.
2. Clasificador de Bosque Aleatorio (Random Forest):
- Elección de Codificación: Los bosques aleatorios pueden funcionar bien tanto con codificación one-hot como con codificación entera. Los bosques aleatorios son robustos y pueden manejar la codificación ordinal si hay un orden significativo. Sin embargo, si deseas evitar posibles interpretaciones erróneas de la ordinalidad, la codificación one-hot es una elección más segura. A menudo es más fácil comenzar con la codificación one-hot y ver si funciona bien para tu conjunto de datos específico.
3. Clasificador de Vecinos Más Cercanos (KNN):
- Elección de Codificación: KNN es un algoritmo basado en la distancia y puede ser sensible a la elección de la codificación. En la mayoría de los casos, se recomienda la codificación one-hot para KNN porque trata cada categoría como una dimensión separada. Sin embargo, si tienes datos ordinales y estás seguro de la significatividad del orden, podrías experimentar con la codificación entera.
4. Clasificador de Máquinas de Soporte Vectorial (SVM):
- Elección de Codificación: Las SVM pueden trabajar con codificación one-hot y codificación entera. Depende del kernel que elijas y la naturaleza de tus datos. Los kernels lineales suelen funcionar bien con la codificación one-hot, mientras que las funciones de kernel como la Función de Base Radial (RBF) pueden manejar ambos tipos de codificación.
En resumen, nosotros usamos codificación one-hot por ser la opción más segura y, como resultado de nuestra investigación, vimos que es la más ampliamente utilizada para la mayoría de los algoritmos de aprendizaje automático, ya que garantiza que cada categoría se trate como una característica separada, dejando claro que no existe una relación ordinal inherente.
- Elegir tres algoritmos de clasificación que se utilizarán en el proyecto. Justificar la selección de cada algoritmo.
Usamos los siguientes 4 modelos de clasificación:
- Utilizar k-cross validation para realizar la clasificación. Seleccionar el valor de "k" y justificar la elección.
La elección del valor de "k" en k-cross validation es un proceso importante ya que influyó en la evaluación del rendimiento de nuestros modelos. La justificación para seleccionar un valor particular de "k" dependió de varios factores, incluidos el tamaño del dataset y nuestros objetivos.
- Dado que tenemos un conjunto de datos pequeño, usamos un valor alto de "k" para aprovechar al máximo nuestros datos y obtener una estimación más estable del rendimiento.
- Esto significa que estamos promediando el rendimiento del modelo sobre más particiones diferentes de nuestros datos. Como resultado, las estimaciones de rendimiento fueron más estables, es decir, menos sensibles a pequeñas variaciones en los datos de entrenamiento y prueba.
- Dado lo anterior, estuvimos dispuestos a obtener la estimación más precisa del rendimiento de nuestros modelos. Es por eso que seleccionamos k=15. Aún cuando esto implico sacrificar un poco de velocidad de cálculo.
- Dado el punto anterior, un valor más alto de "k" significa que realizamos más divisiones del conjunto de datos y, por lo tanto, requerimos más tiempo de cómputo.
- Sabemos que k afecta nuestras estimaciones de rendimiento. Aunque el valor "k = 15 [considerado alto]" nos proporcionó estimaciones de rendimiento más estables, esto fue expensas de una mayor varianza.
- Esto quiere decir que este aumento en la estabilidad tiene un costo potencial. Cuanto mayor era nuestro valor de "k," más pequeños fueron los conjuntos de entrenamiento en cada iteración de la validación cruzada. Con conjuntos de entrenamiento más pequeños, es posible que los modelo no capturaran todas las variaciones y patrones presentes en los datos. Esto llevó a una mayor variabilidad en las estimaciones de rendimiento [como se mostrará a continuación]: esto significa que las métricas varian más entre las diferentes divisiones de los datos.
En resumen, concluímos que es importante entender que existe un equilibrio entre la estabilidad y la capacidad de generalización de nuestros modelo.
| Cross-validation scores: [0.75609756, 0.58536585, 0.775, 0.725, 0.825, 0.625, 0.775, 0.775, 0.825, 0.875, 0.725, 0.75, 0.825, 0.825, 0.775] Logistic Regression Mean Accuracy: 0.76 |
|
| KNN Cross-validation scores [0.70731707, 0.6097561, 0.775, 0.775, 0.825, 0.775, 0.75, 0.775, 0.8, 0.75, 0.775, 0.825, 0.8, 0.8, 0.725] KNN Mean Accuracy: 0.76 |
|
| Cross validation scores [0.70731707, 0.65853659, 0.75, 0.8, 0.825, 0.7, 0.85, 0.8, 0.775, 0.85, 0.75, 0.825, 0.825, 0.825, 0.775] SVM Mean Accuracy: 0.78 |
|
| Cross validation scores Random Forest: [0.70731707, 0.65853659, 0.825, 0.85, 0.775, 0.75, 0.775, 0.725, 0.85, 0.85, 0.825, 0.9, 0.775, 0.85, 0.8] Random Forest Mean accuracy 0.79 |
- Calcular la exactitud, precisión, matriz de confusión, curva ROC y AUC. Explicar cada una de estas métricas.
-
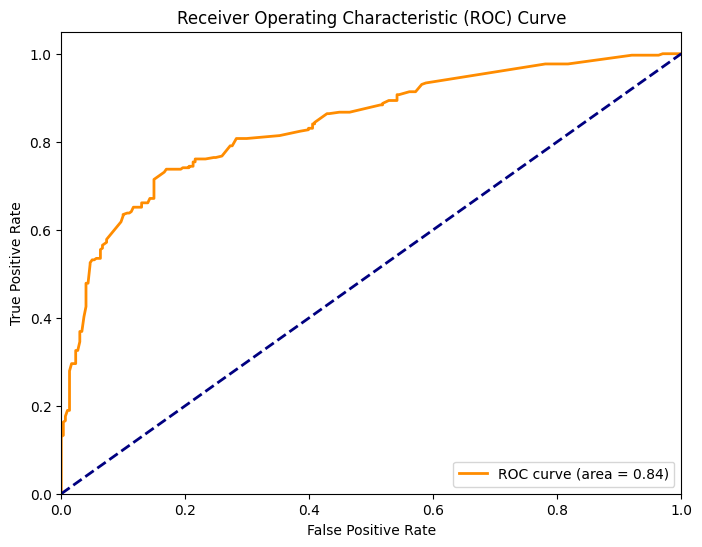
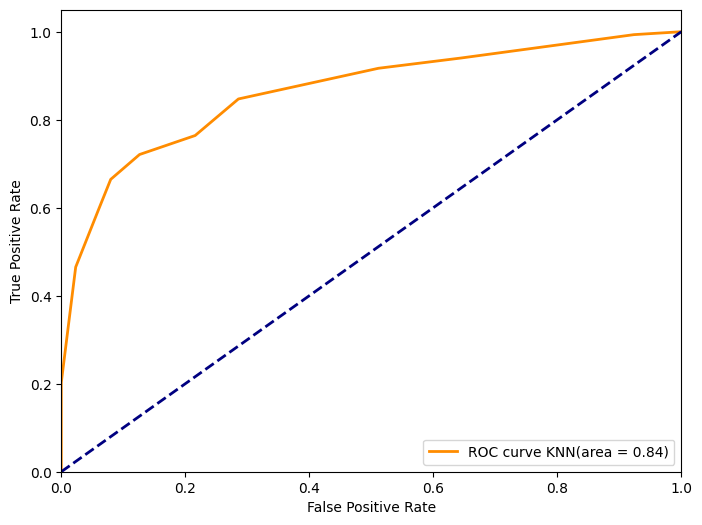
La Curva ROC es una representación gráfica que usamos para evaluar el rendimiento de nuestros modelos de clasificación. Se representa la tasa de verdaderos positivos (Recall) en el eje vertical y la tasa de falsos positivos en el eje horizontal a medida que se varía el umbral de decisión del modelo.
-
En el eje vertical (Recall), mostramos la capacidad del modelo para detectar correctamente los casos positivos en función de diferentes umbrales de probabilidad. Cuanto más alto vemos el punto en la Curva ROC, mejor será es el modelo en la identificación de verdaderos positivos.
-
En el eje horizontal, se muestra la tasa de falsos positivos, que representa la proporción de casos negativos incorrectamente clasificados como positivos en función de diferentes umbrales de probabilidad. Consideramos que tenemos un buen modelo puesto que tenemos una tasa de falsos positivos baja incluso a altos niveles de Recall.
-
AUC Score: 0.84
- Nuestro resultado es 0.84, lo que es bastante positivo. Un AUC de 0.84 sugiere que el modelo de Regresión Logística tiene una buena capacidad de discriminación. Es decir, es efectivo para distinguir entre las dos clases en tu problema de clasificación (supervivientes y no supervivientes).
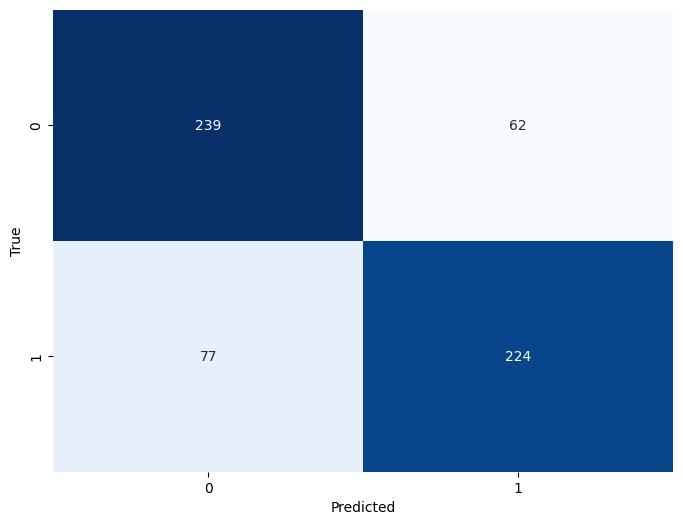
- Verdaderos Positivos (True Positives, TP): Son los casos en los nuestro modelo predijo correctamente la clase positiva. Tenemos 261 verdaderos positivos.
- Falsos Negativos (False Negatives, FN): Son los casos en los que nuestro modelo predijo incorrectamente la clase negativa cuando la verdadera clase era positiva. Tenemos 40 falsos negativos.
- Falsos Positivos (False Positives, FP): Son los casos en los que nuestro modelo predijo incorrectamente la clase positiva cuando la verdadera clase era negativa. Tenemos 46 falsos positivos.
- Verdaderos Negativos (True Negatives, TN): Son los casos en los que nuestro modelo predijo correctamente la clase negativa. Tenemos 255 verdaderos negativos.
-
AUC Score: 0.84
- El valor AUC resume el rendimiento global del modelo KNN utilizando la Curva ROC. Un AUC de 0.84 nos indica que nuestro modelo de KNN también una buena capacidad de discriminación. Al igual que con LogReg, es efectivo para distinguir entre los pasajeros que sobrevivieron y los que no. Sin embargo, podemos tunear hiperparámetros para volver más alto el punto en la Curva ROC.
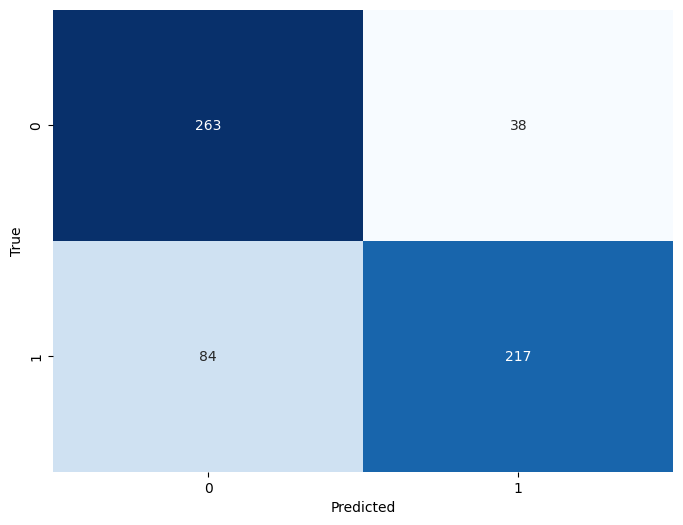
- Verdaderos Positivos (True Positives, TP): Son los casos en los nuestro modelo predijo correctamente la clase positiva. Tenemos 266 verdaderos positivos.
- Falsos Negativos (False Negatives, FN): Son los casos en los que nuestro modelo predijo incorrectamente la clase negativa cuando la verdadera clase era positiva. Tenemos 35 falsos negativos.
- Falsos Positivos (False Positives, FP): Son los casos en los que nuestro modelo predijo incorrectamente la clase positiva cuando la verdadera clase era negativa. Tenemos 87 falsos positivos.
- Verdaderos Negativos (True Negatives, TN): Son los casos en los que nuestro modelo predijo correctamente la clase negativa. Tenemos 214 verdaderos negativos.
-
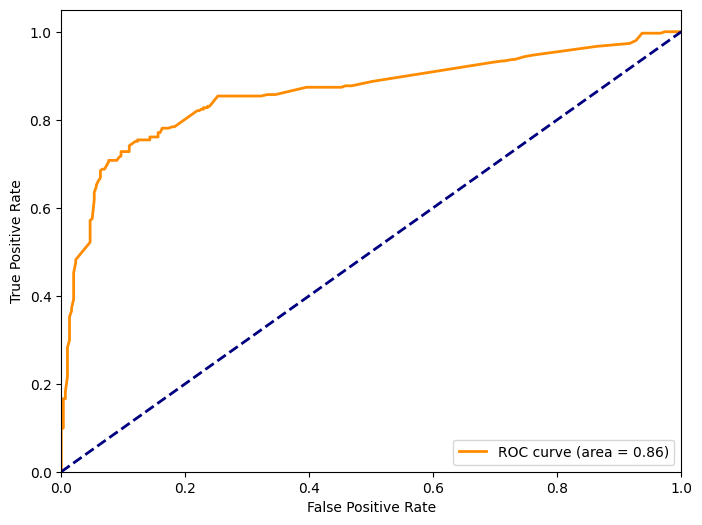
AUC Score: 0.86
- Tenemos un AUC de 0.86 lo cuál es muy positivo y nos sugiere que el modelo de SVM tiene una muy buena capacidad de discriminación. Es un modelo sólido al igual que los 2 previos.
-
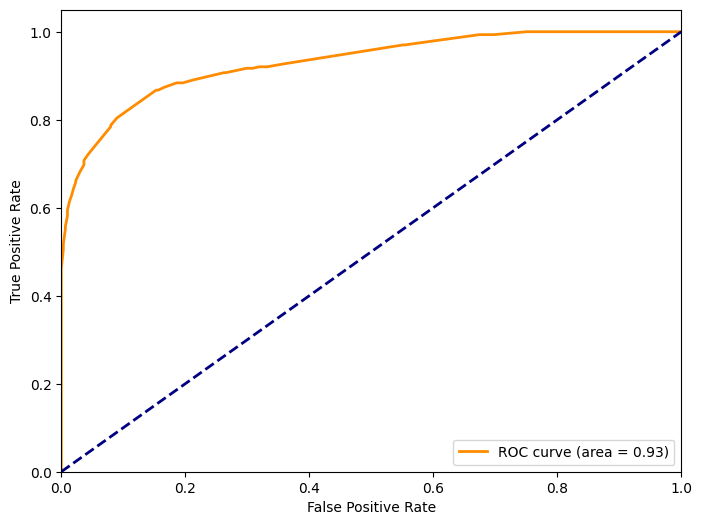
AUC Score: 0.93
- El resultado AUC de 0.93 es excepcionalmente alto, en comparación con nuestros otros 3 modelos. Esto nos sugiere que el modelo de Random Forest Classifier tiene una mayor capacidad de discriminación. En otras palabras, es el más altamente efectivo para distinguir entre los pasajeros que sobrevivieron y los que no.
-
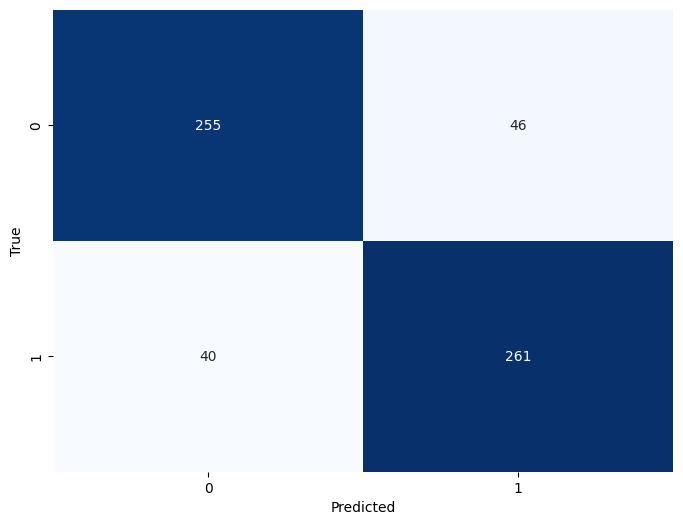
Verdaderos Positivos (True Positives, TP): Son los casos en los nuestro modelo predijo correctamente la clase positiva. Tenemos 255 verdaderos positivos.
-
Falsos Negativos (False Negatives, FN): Son los casos en los que nuestro modelo predijo incorrectamente la clase negativa cuando la verdadera clase era positiva. Tenemos 46 falsos negativos.
-
Falsos Positivos (False Positives, FP): Son los casos en los que nuestro modelo predijo incorrectamente la clase positiva cuando la verdadera clase era negativa. Tenemos 40 falsos positivos.
-
Verdaderos Negativos (True Negatives, TN): Son los casos en los que nuestro modelo predijo correctamente la clase negativa. Tenemos 261 verdaderos negativos.
-
Con base en estas métricas, determinar el mejor clasificador y justificar la elección.
El mejor clasificador fue: Random Forest Classifier. El motivo es dado los resultados de las métricas. Todo demuestra un mejor desempeño por parte de Random Forest que por parte de Logistic Regression, Support Vector Machine o K Nearest Neighbors.