Tema 2 - Matrix Multiplication

Requirement

Sa se efectueze urmatoarea operatie cu matrice: C = A * B * B' + A' * A

A si B matrice patratice de double de dimensiune N * N
A este superior triunghiulara

Blas implementation

Pentru implementarea cu BLAS am folosit functiile cblas_dtrmm(double triunghiular matrix multiplication) si cblas_dgemm.

Am efectuat operatiile in ordinea in care ele apar:

AB = A * B, folosind proprietatea ca A este superior triunghiulara
ABBt = AB * B', folosind inmultirea obisnuita(AB nu este superior triunghiulara)
AtA = A' * A, folosind proprietatea ca A este superior triunghiulara
la sfarsit, am adunat cele 2 matrice in matricea C

NEOPT implementation

implementarea neoptimala a operatiilor
pentru realizarea ei, am inmultit matricele cu cele 3 for-uri clasice.
la inmultirile cu matricea A (A * B si A' * A) am tinut cont de faptul ca A este superior triunghiulara, schimband range-ul pentru indexul liniilor/coloanelor ce se acceseaza din matricea A

OTP implementation

implementarea optimizata manual
pentru a micsora timpul de rulare, am optimizat timpul de acces la memorie:
- toate variabilele folosite(indecsii si variabile sum) sunt declarate ce keyword-ul register
- pentru a face mai putine accese la memoria principala, suma se face in variabila sum, declarata ca register, accesandu-se o singura data adresa de memorie unde va fi stocat rezultatul

A * B multiplication

avand in vedere ca A este superior triunghiulara, nu are sens parcurgerea coloanelor mai jos de diagonala principala(deoarece elementele de sub diagonala principala sunt 0). De aceea, indicele pleaca de la i

A' * A multiplication

Se va folosi proprietatea ca matricea A este superior triughiulara
Transpusa matricei A va fi inferior triunghiulara, iar daca vom analiza inmultirea celor 2 matrice, se poate observa ca fiecare element din rezultat contine in compozitia lui doar elemente ce au linia minimul dintre i si j(deoarecele restul elementelor sunt 0). Practic, cu cat ne apropiem de coltul dreapta jos al matricei, cu atat vom avea mai multe elemente inmultite, doarece aici nu sunt zerouri.

Cachegrind

varianta neoptimizata

==29711== D   refs:      2,759,590,560  (2,639,432,484 rd   + 120,158,076 wr)
==29711== D1  misses:       52,020,258  (   51,949,081 rd   +      71,177 wr)
==29711== LLd misses:          113,079  (       62,023 rd   +      51,056 wr)
==29711== D1  miss rate:           1.9% (          2.0%     +         0.1%  )
==29711== LLd miss rate:           0.0% (          0.0%     +         0.0%  )

varianta optimizata

==29710== D   refs:        813,056,452  (810,391,322 rd   + 2,665,130 wr)
==29710== D1  misses:       52,191,920  ( 51,945,369 rd   +   246,551 wr)
==29710== LLd misses:          113,078  (      2,026 rd   +   111,052 wr)
==29710== D1  miss rate:           6.4% (        6.4%     +       9.3%  )
==29710== LLd miss rate:           0.0% (        0.0%     +       4.2%  )

Daca inspectam output-ul cachegrind, se poate observa ca desi varianta optimizata are o rata de miss mai mare(9.3% vs 0.1%), numarul de read-uri este de aproximativ 3 ori mai mic, iar numarul de write-uri de 45 ori mai mic.

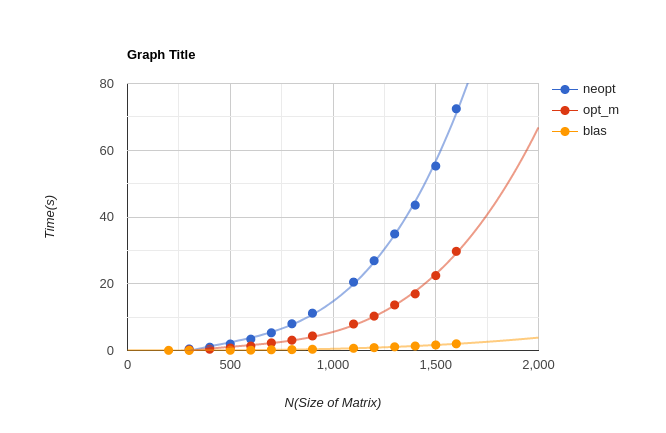
Time Comparison

Graficul prezentat este facut pe baza urmatoarelor valori:

Matrix Size	NEOPT	OPT	BLAS
300	0.463843	0.193456	0.027869
400	0.990357	0.384109	0.046227
500	1.943393	0.743817	0.073024
600	3.401591	1.324224	0.112802
700	5.308603	2.282834	0.216528
800	8.003953	3.089454	0.260059
900	11.181709	4.357147	0.369597
1100	20.481323	7.935046	0.663317
1200	26.899799	10.296909	0.850983
1300	34.921803	13.646874	1.098453
1400	43.564064	16.964916	1.342515
1500	55.268566	22.453712	1.653533
1600	72.434303	29.709724	2.001687

Analizand datele de la cele 3 implementari, se poate observa:

implementarea cu blas este de aproximativ 12 ori mai rapida decat varianta opt_m
implementarea optima neoptima este de aproximativ 2.6 ori mai rapida decat opt_m.

Bibliography

BLAS

filimonadrian/matrix-mult