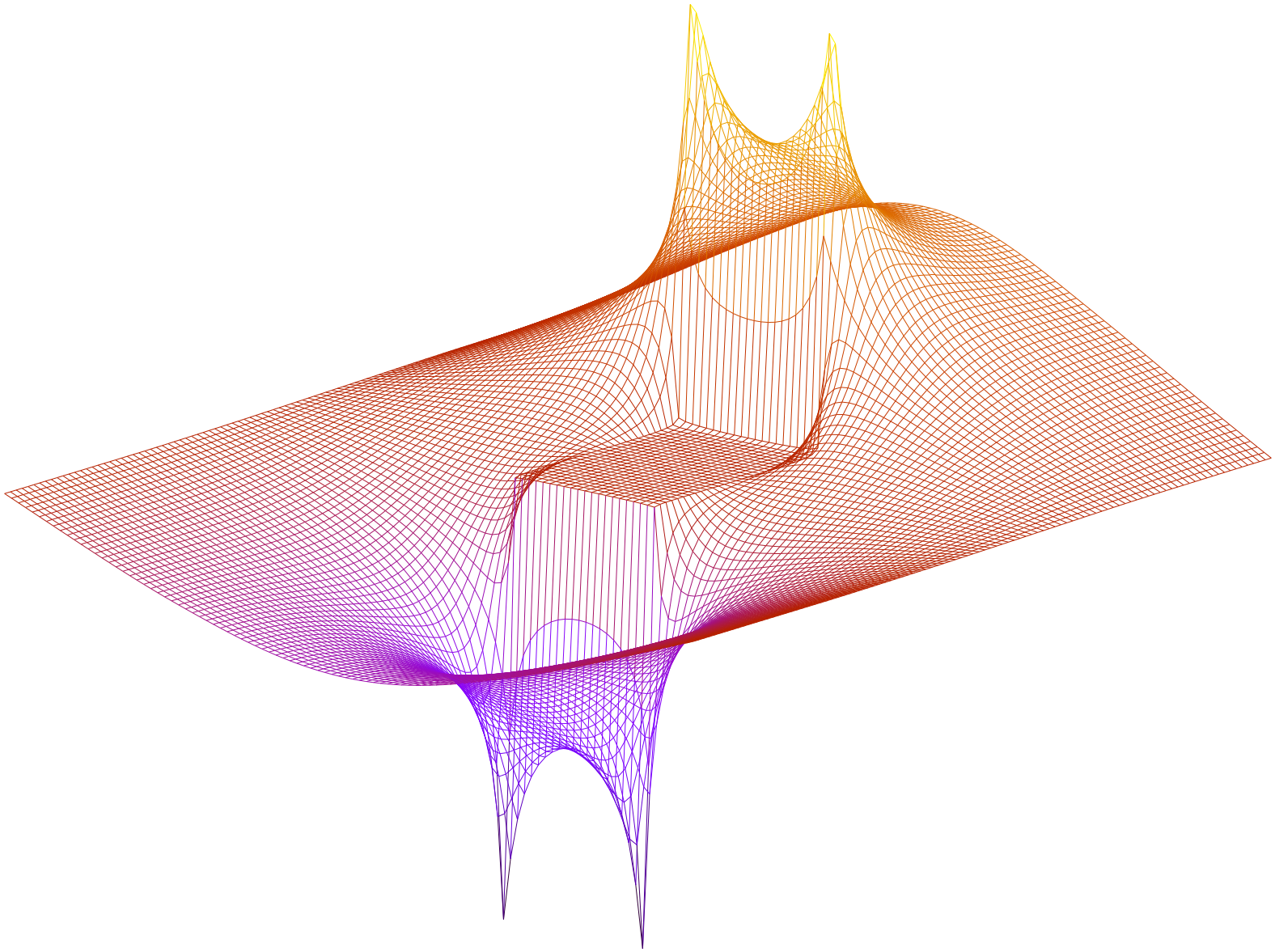
This code solves the Laplace equation ∇2u = 0 for electrostatic potentials u bounded in concentric regions using the Gauss–Seidel algorithm with successive over-relaxation.
Clone and make && make clean.
If building on macOS, first brew install argp-standalone and
export CFLAGS="$CFLAGS -I/usr/local/include/"
export LDFLAGS="$LDFLAGS -L/usr/local/lib/ -largp"to make GLIBC argument parsing available.
./seidel with no arguments will print the (automatically chosen) parameters and the value of the double integral of E2 over the region, a measure of the total electric field.
Run with --help to expose the optional flags.
Usage: seidel [-cpqrt?] [-a a] [-b b] [-n n] [-w w] [--xboundary=a]
[--yboundary=b] [--clean] [--size=n] [--print] [--norelax]
[--relax] [--translate] [--omega=w] [--help] [--usage]
The boundary point (a, b) defines the north-west point of the inner boundary.
./seidel --print produces data files of the form
x y f(x,y)
for the potential (u.dat), the x- and y- components of the electric field (ex.dat, ey.dat) and a file cs.dat of the form
y E_x E_y
which is a cross-section of the electric field at x = 0.5 * n. These files can be removed with --clean (and also with make delete). Run the .plt scripts to plot the results.
The --translate option outputs the value of the integral L (above) as the inner boundary is translated vertically through the region.
The program over-relaxes by default (using successive over-relaxation parameter ω = 1.92, the optimum value for the default configuration). This can be disabled with --norelax (which sets ω = 1), assigned with --omega or calculated with --relax, which prints the value of ω and the number of iterations required for the solution to converge until it hits the minimum.