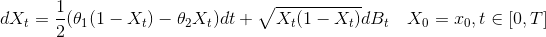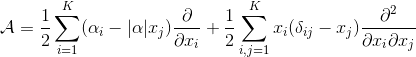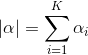flavda/ExactWrightFisher.jl

Exact simulation of the Wright--Fisher diffusion

ExactWrightFisher

Exact simulation of the neutral Wright-Fisher diffusion.

Implementation of the exact simulation scheme of Jenkins, P. A., Spano, D., & Others. (2017). Exact simulation of the Wright--Fisher diffusion. The Annals of Applied Probability, 27(3), 1478–1509.

We consider a continuous time version of the multi-dimensional Wright-Fisher model, which is a stochastic differential equation.

The 1-dimensional version of the Wright-Fisher model is defined by the following equation:

The multi-dimensional version is more easily expressed with the generator of the stochastic process:

where .

The scheme uses a retrospective approach similar to the exact algorithms of Beskos (2005), and employs the alternating series trick by Devroye to sample from an infinite series expansion of the transition function for the Wright-Fisher process.

This scheme may become inefficient for very short time steps, but a good approximation may then be used.

A graphical comparison of simulated samples against the stationary distribution is available here.

How to install the package

Press ] in the Julia interpreter to enter the Pkg mode and input:

pkg> add ExactWrightFisher

How to use the package

The package is developed for Julia 1.0. An R/Rcpp implementation is available on request.

To load the package, input:

using ExactWrightFisher, Random, Distributions

Then to sample from the transition density of a K dimensional Wright Fisher process, do:

Random.seed!(0);
α_vec = [1.2,1.4,1.3]
Wright_Fisher_K_dim_exact_transition([0.2, 0.4, 0.4], 0.5, α_vec)
3-element Array{Float64,1}:
 0.37638432059656973
 0.18253800610053464
 0.44107767330289566

To sample a full trajectory, do:

Random.seed!(0);
α_vec = [1.2,1.4,1.3]
Wright_Fisher_K_dim_exact_trajectory([0.2, 0.4, 0.4], range(0, stop = 1, length = 10), α_vec)
3×11 Array{Float64,2}:
 0.2  0.2  0.288971  0.156417  0.0282289  …  0.443116  0.416719  0.435391
 0.4  0.4  0.302104  0.526393  0.57872       0.359188  0.36929   0.340048
 0.4  0.4  0.408926  0.31719   0.393051      0.197697  0.213991  0.22456

See also Wright_Fisher_exact_transition, and Wright_Fisher_exact_trajectory for 1 dimensional Wright-Fisher processes.

Small time steps (dt <= 0.05)

The exact algorithm may hang for small time steps, in practice around 0.05.

However, in this case a very good normal approximation of the transition function is available.

Functions that use the exact algorithm for large time steps and fall back to the approximation for small time steps are available as: Wright_Fisher_exact_transition_with_t005_approx, Wright_Fisher_exact_trajectory_with_t005_approx, Wright_Fisher_K_dim_transition_with_t005_approx, Wright_Fisher_K_dim_trajectory_with_t005_approx.

References:

• Beskos, A. and Roberts, G. O. (2005). Exact simulation of diffusions. The Annals of Applied Probability 15, 2422–2444.
• Devroye, L. (1986). Nonuniform Random Variate Generation. Springer, New York.
• Jenkins, P. A., Spano, D., & Others. (2017). Exact simulation of the Wright--Fisher diffusion. The Annals of Applied Probability, 27(3), 1478–1509.