Vectorised implementation of the Histogram of Oriented Gradients
Clone the repository and cd there:
git clone https://github.com/JeanKossaifi/python-hog
cd python-hogThen install the package (here in editable mode with -e or equivalently --editable:
pip install -e .Simply run
pip install git+https://github.com/JeanKossaifi/python-hogBecause of time-constraints the code might not be as clear as it should be but here is the idea behind it:
Assuming we have a gray-scale image represented as an ndarray of shape (sy, sx).
We want to compute the HOG features of that image with nbins orientation bins.
First, we interpolate between the bins, resulting in a (sy, sy, nbins) array.
We then interpolate spatially. The key observation is that in the end (after interpolation), we do not care about the position of the orientation vectors since all orientation vector for a given cell are going to be summed to obtain only one histogram per cell. We can thus virtually divide each cell in 4, each part being interpolated in the 4 diagonally adjacent sub-cells. As a result, each of the 4 sub-cell will be interpolated once in the same cell, and once in the 3 adjacent cells (which is exactly what interpolation is). The only thing to do is to multiply by the right coefficient.
To illustrated: We sum 4 times in the 4 diagonal directions. The coefficient for the sum can be represented by a single matrix which is turned.
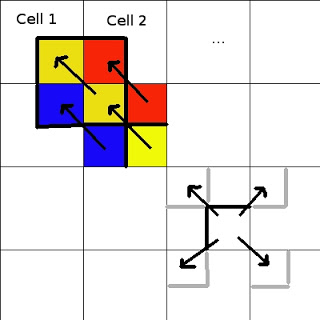
Finally the histograms in each cell are summed to obtain the (n_cells_x, n_cells_y, nbins) desired orientation_histogram (which can be further normalise block-wise).