Hash Table

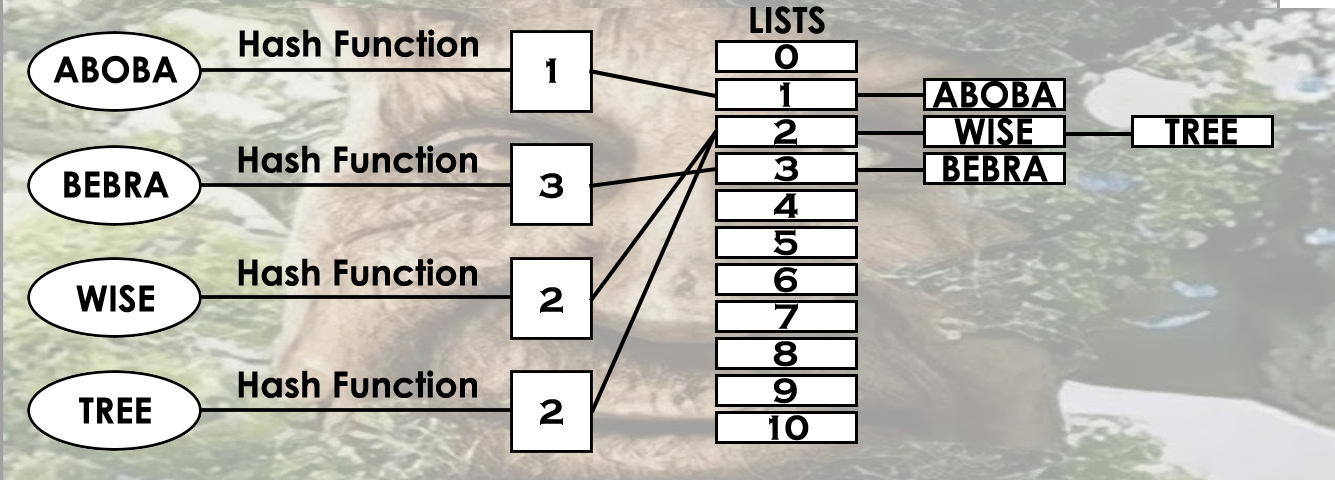
For average hash table enjoyers.

Introduction

A hash table is an abstract data type that maps keys set to values set using hash function.

However, there is a disadvantage, which is that two keys can have the same hash. This is called collision. So we are going to use chain method to avoid it. More information about it can be found here: Click!

It can be represented in the following form:

It is also important to mention that size of hash table is a prime number: Why is it so?

Overview

Goals of this project:

Research the properties of hash functions and choose the best of them, depending on distribution;
Implement different types of assembly optimizations to speed up the searching process.

Technical parameters:

CPU: Intel Core i5 11300H (AVX instructions: AVX-512)
Compiler: g++ (Ubuntu 11.3.0-1ubuntu1~22.04) 11.3.0
Table size: 1009
Keys set: Words of "The adventures of Sherlock Holmes" (41935 unique words)
Utilities used: Valgrind, Callgrind, Kcachegring

P.S. Average CPU temperature was 27.9 $^0C$

First part. Choose your fighter.

It’s obvious that the more collisions we have - the slower search of values we'll get. So we need to select the function with the least number of collisions of these:

1) constHash

This wonderful function always gives the same value on different keys:

size_t constHash (const char *string)
{
    return 1;
}

Distribution

Kinda fun, but it's the worst hash function I can imagine...

2) firstCharAsciiHash

Returns ASCII code of string's first symbol:

size_t firstCharAsciiHash (const char *string)
{
    return (size_t) string[0];
}

Distribution

This function is better than previous and it can be used on small text. However, the large text doesn't give a chance to it.

3) stringLengthHash

Returns length of string:

size_t stringLengthHash (const char *string)
{
    return strlen(string);
}

Distribution

We have even more collisions on that function. English words are not very long as we can see.

4) charSumHash

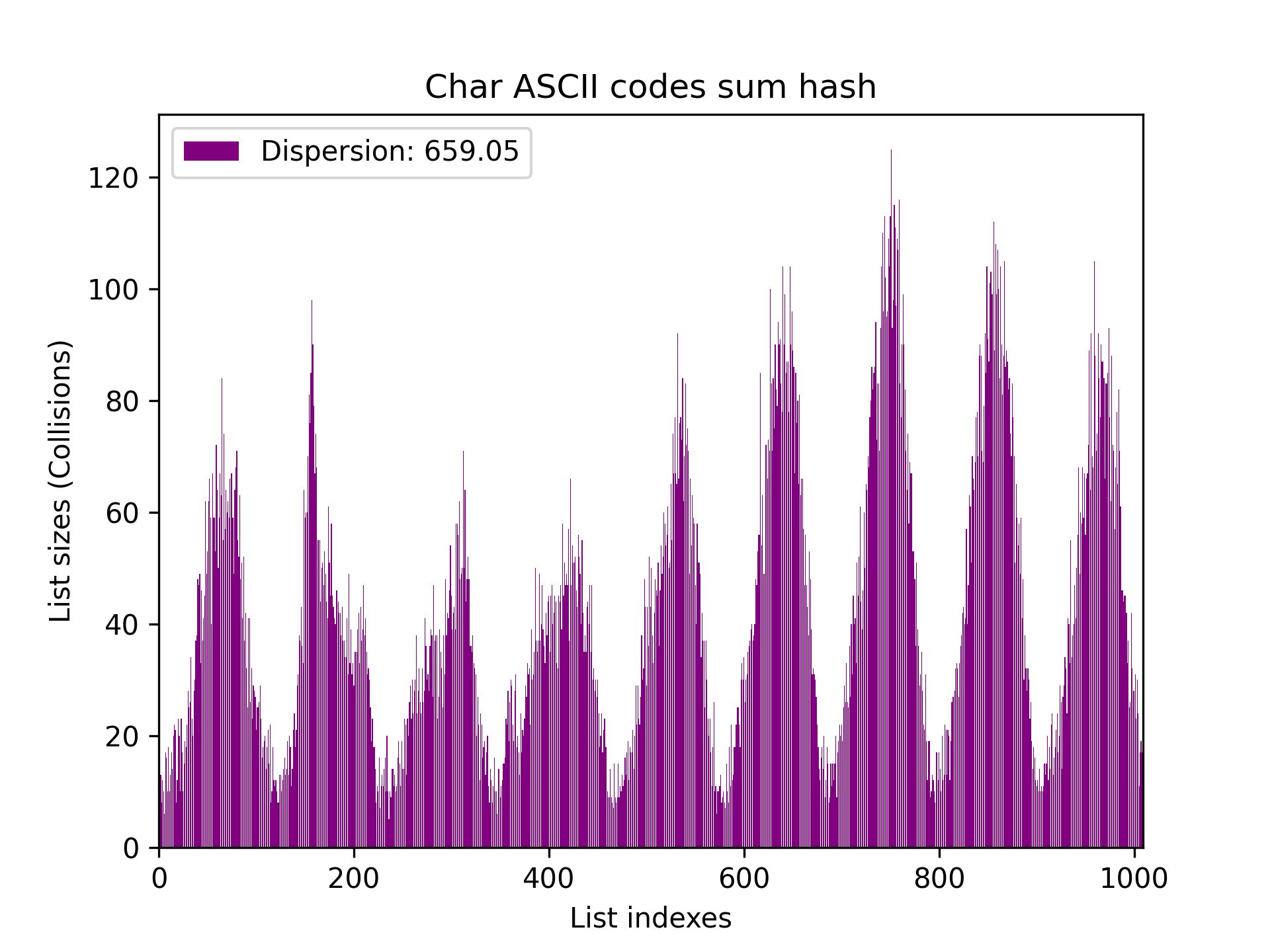
Returns sum of symbols ASCII codes:

size_t charSumHash (const char *string)
{
    size_t hash = 0;

    for (size_t symbolIndex = 0; string[symbolIndex] != '\0'; symbolIndex++)
        hash += (size_t) string[symbolIndex];
    
    return hash;
}

Distribution

Dispersion became slightly better (~250).

5) ROL Hash

For average left Twix stick enjoyers:

size_t rollingLeftHash (const char *string)
{
    size_t hash = 0;

    for (size_t symbolIndex = 0; string[symbolIndex] != '\0'; symbolIndex++)
    {
        size_t firstPart  = hash << 1;
        size_t secondPart = hash >> 31;

        hash += (firstPart | secondPart) ^ (size_t) string[symbolIndex];
    }

    return hash;
}

Distribution

Less dispersion - more search speed! (More speed to the God of the speed u-ha-ha-ha)

6) ROR Hash

For average right Twix stick enjoyers:

size_t rollingRightHash (const char *string)
{
    size_t hash = 0;

    for (size_t symbolIndex = 0; string[symbolIndex] != '\0'; symbolIndex++)
    {
        size_t firstPart  = hash >> 1;
        size_t secondPart = hash << 31;

        hash += (firstPart | secondPart) ^ (size_t) string[symbolIndex];
    }

    return hash;
}

Distribution

Interesting result: ROR's Dispersion is less than the ROL's Dispersion by ~6 times. Usually the ROL's results are better. Apparently the sample has a big impact.

7) polynomialRollingHash

Based hash function for string hashing:

size_t polynomialRollingHash (const char *string)
{
    static const size_t power = 53; // Good value for letters in upper and lower cases

    size_t hash = 0;
    size_t currentPower = 1;

    for (size_t symbolIndex = 0; string[symbolIndex] != '\0'; symbolIndex++)
    {
        hash += (size_t) string[symbolIndex] * currentPower;

        currentPower *= power;
    }

    return hash;
}

Distribution

It gives dispersion about ~42. Bingo! I will use this hash function for the next part, because it has a great potential for optimizations and small dispersion.

Second part. Optimizations.

We have already selected hash function, so now we need to consider ways to speed up hash table.

We will use valgrind with callgrind tool and kcachegrind for callgrind output vizualization.

P.S. All measurements are made 4 times for better accuracy.

Baseline

Let's take a look at baseline.

Version	Time	Absolute speedup	Relative speedup
Baseline	4.11 +- 0.03	1	1

Kcachegrind output:

First we will try to use compiler optimization -O2, to boost our perfomance.

Compiler optimization -O2

Version	Time	Absolute speedup	Relative speedup
Baseline	4.11 +- 0.03	1	1
-O2	2.675 +- 0.019	1.54	1.54

Profiler data:

As we see from profiler __strcmp_avx2 is on first place in Self rating. So we need to optimize the element compare function (strcmp) to improve performance.

1 assembler optimization

Optimizing strcmp with inline assembler:

Code

int strcmpASM (const char *string1, const char *string2)
{
    int result = 0;

    asm volatile 
    (
        ".intel_syntax noprefix;"

        "1:"
        "lodsb;"
        "scasb;"
        "jne 2f;"

        "test al, al;"
        "jne 1b;"

        "xor eax, eax;"
        "jmp 3f;"

        "2:"
        "dec edi;"
        "sbb eax, eax;"

        "3:"
        ".att_syntax" 
        : "=a" (result)
        : "S" (string1), "D" (string2)
        : "memory"
    );

    return result;
}

Version	Time	Absolute speedup	Relative speedup
Baseline	4.11 +- 0.03	1	1
-O2	2.675 +- 0.019	1.54	1.54
first opt.	0.4865 +- 0.0011	8.45	5.5

Profiler data:

We see that our hash function is bottleneck now. Let's try to use our own hash function rewrited on assembler.

2 assembler optimization (fail)

Version	Time	Absolute speedup	Relative speedup
Baseline	4.11 +- 0.03	1	1
-O2	2.675 +- 0.019	1.54	1.54
first opt.	0.4865 +- 0.0011	8.45	5.5
second opt.	0.6185 +- 0.0025	6.65	0.77

Profiler data:

Let's see this:

Code

global polynomialRollingHashASM

;~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
; Pollynomial Rolling Hash Function on x86-64 asm
;~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
; Entry:    RDI = Address of string
; Exit:     RAX = Hash value
; Destroys: None
; Expects:  Constant number 'Power'
;~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

polynomialRollingHashASM:  
        push rdi    ; Saving registers values
        push rbx
        push rcx
        push rdx
        push r8
        push r9

        mov rax, 1      ; Moving 1 to register for current power
        mov r8, Power   ; Moving power to register

        xor rbx, rbx    ; Zeroing register for current symbol
        xor rcx, rcx    ; Zeroing register for hash

.next:  mov bl, byte [rdi]  ; Loading current symbol in BL
        test bl, bl         ; Checking that current symbol != '\0'
        jz .end

        mov r9, rax         ; Saving current power

        mul rbx             ; Mulling current power and current symbol
        add rcx, rax        ; Adding that value to hash

        mov rax, r9         ; Restoring current power

        mul r8              ; Increasing power
        inc rdi             ; Going to next symbol
        jmp .next           ; Going to next iteration

.end:   mov rax, rcx    ; Saving hash value to RAX

        pop  r9         ; Restoring registers values
        pop  r8
        pop  rdx 
        pop  rcx
        pop  rbx
        pop  rdi 

        ret

As we can see this function slows down our program and profiler shows that it is still a bottleneck. Let's try to use AVX instructions for hash function optimization.

3 assembler optimization

Version	Time	Absolute speedup	Relative speedup
Baseline	4.11 +- 0.03	1	1
-O2	2.675 +- 0.019	1.54	1.54
first opt.	0.4865 +- 0.0011	8.45	5.5
second opt.	0.6185 +- 0.0025	6.65	0.77
third opt.	0.437 +- 0.008	9.41	1.42

Profiler data:

Code

;~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
; crc32 on x86-64 asm + AVX2
;~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
; Entry:    RDI = Address of string
; Exit:     RAX = Hash value
; Destroys: None
; Expects:  None
;~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

global crc32AVX

crc32AVX:       xor rax, rax                    ; Zero register for hash

                crc32 rax, qword [rdi + 0 * 8]  ; Counting hash
                crc32 rax, qword [rdi + 1 * 8]
                crc32 rax, qword [rdi + 2 * 8]
                crc32 rax, qword [rdi + 3 * 8]

                ret

In this optimization loop we replaced polynomial rolling hash function with crc32 hash function (Intel Intrinsics Guide). Speedup relatively 1 optimization is 1.11 it isn't too much and according to profiler the bottleneck now is list search function, so we won't continue optimizing.

Conclusion

It turns out, that not every optimization speeds up the program, sometimes it only slows it down. (c) Dodokek

Ded's coefficient is 409

flopsreallygotit/HashTable

Hash Table

Introduction

Overview

First part. Choose your fighter.

1) constHash

2) firstCharAsciiHash

3) stringLengthHash

4) charSumHash

5) ROL Hash

6) ROR Hash

7) polynomialRollingHash

Second part. Optimizations.

Baseline

Compiler optimization -O2

1 assembler optimization

2 assembler optimization (fail)

3 assembler optimization

Conclusion