The peculiar motion of galaxies on an expanding background make the translation from redshifts to distances non-trivial, due to the additional Doppler effect. When we measure the clustering of galaxies without removing the effect of their motions, we are measuring a combination of their actual clustering and their pairwise velocity distribution [1],
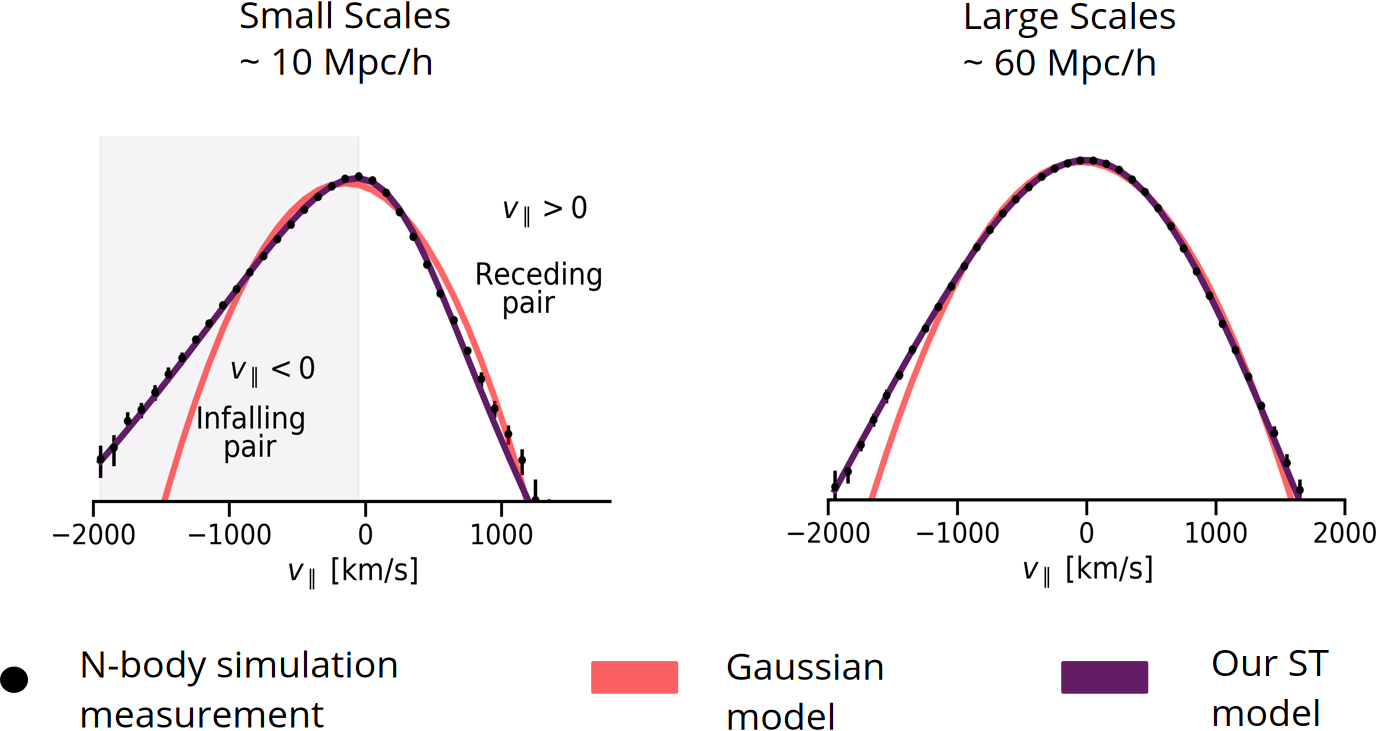
In the following figure, we show the pairwise velocity distribution measured on N-body simulations for different pair separations. The PDF is highly non-Gaussian, it shows both skewness and heavy tails
State-of-the-art models approximate the pairwise velocity distribution by a Gaussian [2], [3].
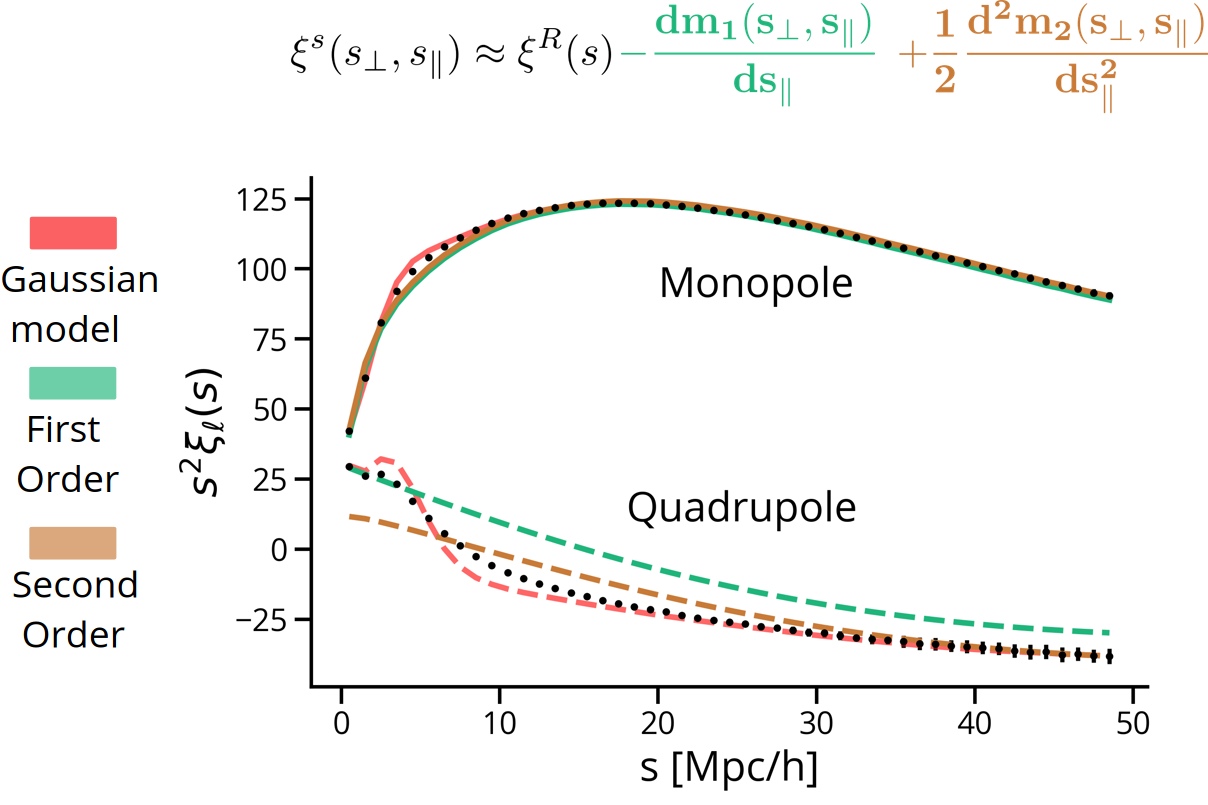
These models can reproduce the monopole and quadrupole up to scales of about 30 Mpc/h. But if we have shown that the PDF is strongly non-Gaussian, why does the Gaussian model work so well?
We can Taylor expand the integral over the pairwise velocity distribution up to second order, which can in turn be written as an expansion in terms of its first two moments, the mean m1 and the dispersion m2,
It turns out that any distribution with the right first two moments reproduces the redshift space clustering up to quasi linear scales. The actual pairwise velocity distribtuion is strongly non-Gaussian.
On small scales, where statistical errors are the smallest, the accuracy of the Gaussian model degrades very quickly. To improve on it, we need to model the pairwise distribution with a PDF that produces higher-order moments. In particular, non-zero skewness and high kurtosis.
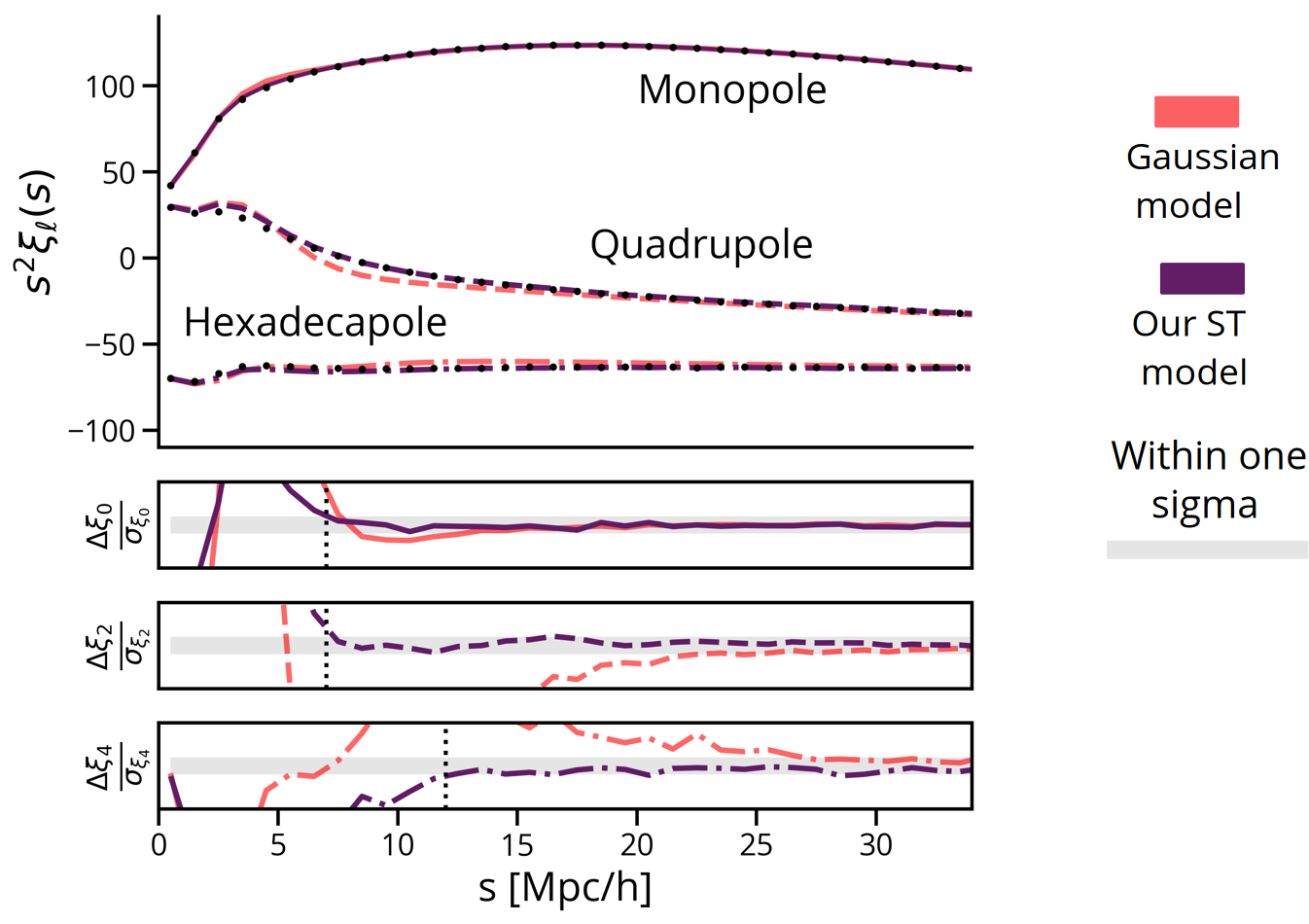
The Skewed Student-t (ST) [4] distribution has exactly these properties. We find its parameters by matching its first four momentsto the ones measured in the simulation. These are the resulting multipoles in redshift space,
Including non-Gaussian features in the velocity pairwise distribution improves the modelling of the redshift space monople and quadrupole to within 1% up to scales of 10 Mpc/h.
The ultimate success of the model relies on the prediction of the pairwise velocity moments. Further work needs to be done to predict these from theory within the required accuracy.
** Under construction, will be released soon **
[1] Scoccimarro, R. 2004, prd, 70, 083007
[2] Reid, B., White, M. 2011, mnras, 417, 191
[3] Wang, L., Reid, B., White, M. 2014, mnras, 437, 588
[4] Azzalini, A., Capitanio, A. 2009, arXiv e-prints, arXiv:0911.2342