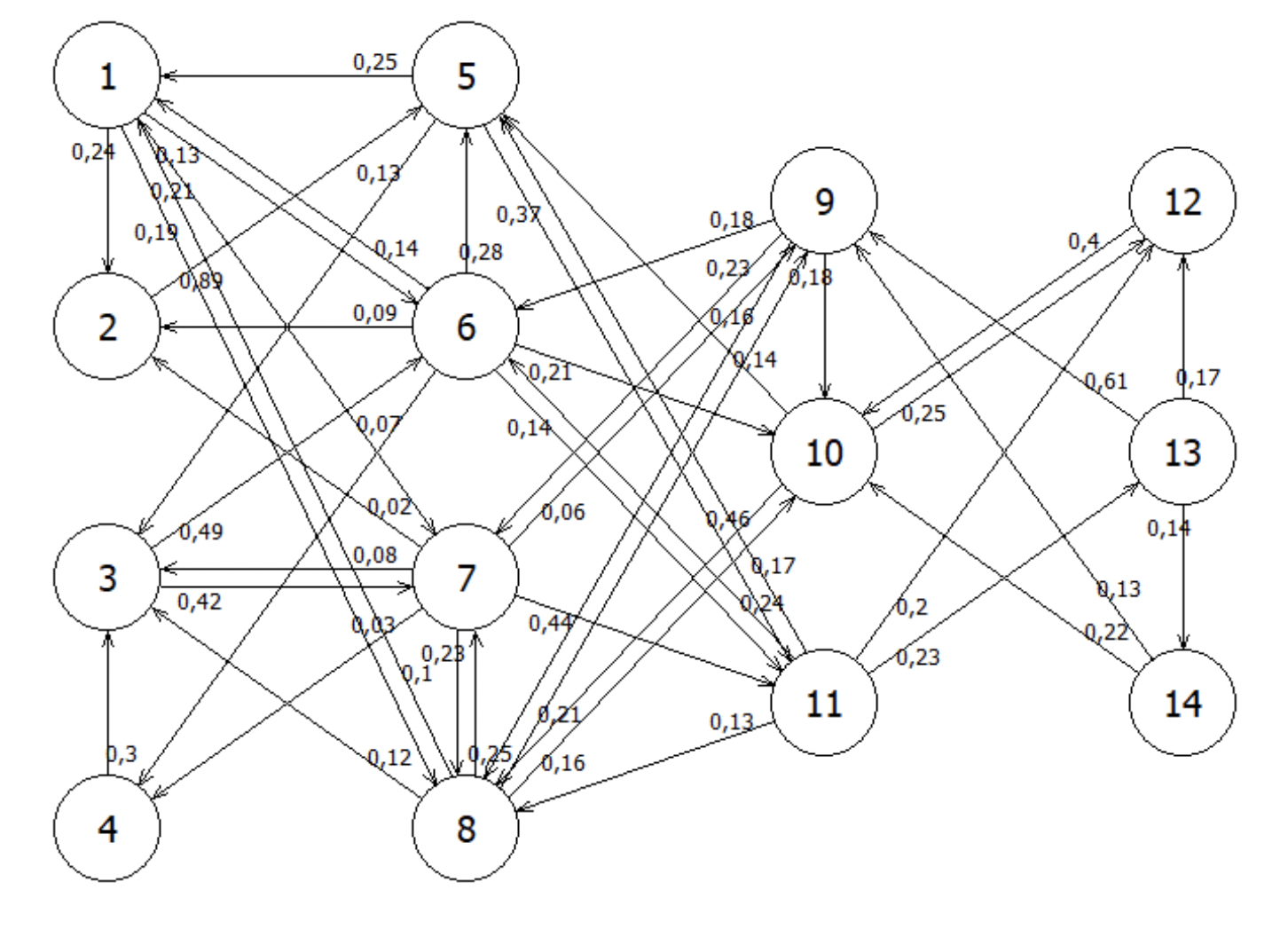
Система имеем 14 дискретных состояний. Изменение состояний происходит в дискретные моменты времени с заданной вероятность. Схема марковского процесса изображена на рисунке.
 Требуется определить:
Требуется определить:
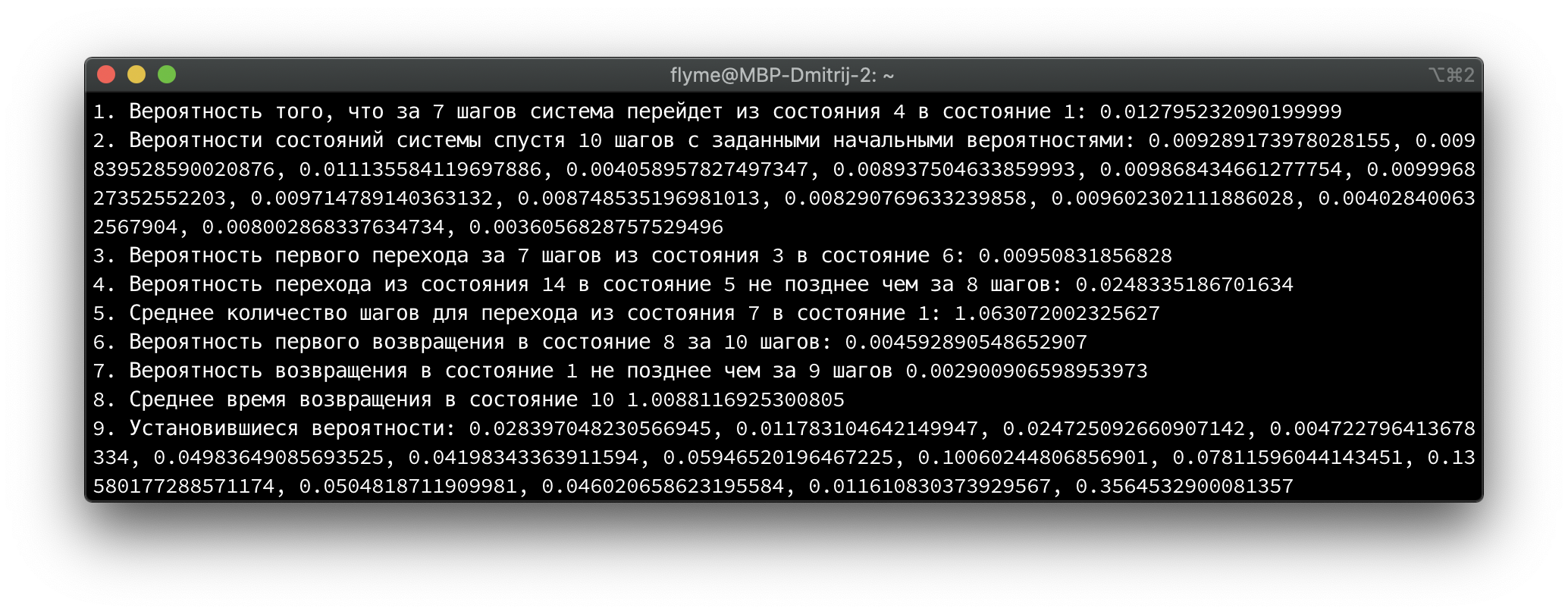
- Вероятность того, что за 7 шагов система перейдет из состояния 4 в состояние 1;
- Вероятности состояний системы спустя 10 шагов, если в начальный момент вероятность состояний были следующими A=(0,08;0,1;0,13;0,09;0,08;0,01;0,1;0,02;0,12;0,05;0,09;0,05;0,06;0,02);
- Вероятность первого перехода за 7 шагов из состояния 3 в состояние 6;
- Вероятность перехода из состояния 14 в состояние 5 не позднее чем за 8 шагов;
- Вреднее количество шагов для перехода из состояния 7 в состояние 1;
- Вероятность первого возвращения в состояние 8 за 10 шагов;
- Вероятность возвращения в состояние 1 не позднее чем за 9 шагов;
- Среднее время возвращения в состояние 10;
- Установившиеся вероятности.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.0 | 0.24 | 0.0 | 0.0 | 0.0 | 0.13 | 0.21 | 0.19 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2 | 0.0 | 0.0 | 0.0 | 0.0 | 0.89 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.49 | 0.42 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 4 | 0.0 | 0.0 | 0.3 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 5 | 0.25 | 0.0 | 0.13 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.37 | 0.0 | 0.0 | 0.0 |
| 6 | 0.14 | 0.09 | 0.0 | 0.07 | 0.28 | 0.0 | 0.0 | 0.0 | 0.0 | 0.21 | 0.14 | 0.0 | 0.0 | 0.0 |
| 7 | 0.0 | 0.02 | 0.08 | 0.03 | 0.0 | 0.0 | 0.0 | 0.23 | 0.06 | 0.0 | 0.44 | 0.0 | 0.0 | 0.0 |
| 8 | 0.1 | 0.0 | 0.12 | 0.0 | 0.0 | 0.0 | 0.25 | 0.0 | 0.21 | 0.16 | 0.0 | 0.0 | 0.0 | 0.0 |
| 9 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.18 | 0.23 | 0.16 | 0.0 | 0.18 | 0.0 | 0.0 | 0.0 | 0.0 |
| 10 | 0.0 | 0.0 | 0.0 | 0.0 | 0.14 | 0.0 | 0.0 | 0.46 | 0.0 | 0.0 | 0.0 | 0.25 | 0.0 | 0.0 |
| 11 | 0.0 | 0.0 | 0.0 | 0.0 | 0.17 | 0.24 | 0.0 | 0.13 | 0.0 | 0.0 | 0.0 | 0.2 | 0.23 | 0.0 |
| 12 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.4 | 0.0 | 0.0 | 0.0 | 0.0 |
| 13 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.61 | 0.0 | 0.0 | 0.17 | 0.0 | 0.14 |
| 14 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.13 | 0.22 | 0.0 | 0.0 | 0.0 | 0.0 |
import csv
from abc import ABCMeta, abstractmethod
from functools import lru_cache
from numpy import array, zeros, linalg, dot, eye
from numpy.linalg import matrix_power
class Markov(metaclass=ABCMeta):
matrix: array
def __init__(self, matrix: array):
self.matrix = matrix
@classmethod
def read_from_file(cls, filename: str) -> "Markov":
"""
Открывает CVS файл и преобразует в array
:param filename:
:return:
"""
with open(filename, encoding="utf-8") as file:
return cls(array([list(map(float, row)) for row in csv.reader(file)]))
@abstractmethod
def probability_of_switching_to_state(self, of: int, to: int, n: int):
pass
@abstractmethod
def probabilities_of_system_states_in_n_steps(
self, n: int, start_step: array
) -> array:
pass
@abstractmethod
def make_step_in_matrix(self, matrix: array) -> array:
pass
@abstractmethod
def probability_of_the_first_transition(self, of: int, to: int, n: int) -> float:
pass
@abstractmethod
def probability_of_transition_no_later_than(
self, of: int, to: int, n: int
) -> float:
pass
@abstractmethod
def average_number_of_steps_for_the_transition(self, of: int, to: int) -> float:
pass
@abstractmethod
def probability_of_first_return(self, of: int, n: int) -> float:
pass
@abstractmethod
def probability_of_return_no_later_than(self, of: int, n: int) -> float:
pass
@abstractmethod
def average_time_of_return(self, of: int) -> float:
pass
@abstractmethod
def steady_state_probability(self):
pass
class MarkovProcess(Markov):
def probability_of_switching_to_state(self, of: int, to: int, n: int) -> float:
"""
Вероятность перехода в состояние
:param of:
:param to:
:param n:
:return:
"""
return matrix_power(self.matrix, n)[of - 1, to - 1]
def probabilities_of_system_states_in_n_steps(
self, n: int, start_step: array
) -> array:
"""
Вероятности состояний системы через n шагов с начальными данными
:param n:
:param start_step:
:return:
"""
return dot(matrix_power(self.matrix, n), start_step)
def make_step_in_matrix(self, matrix: array) -> array:
"""
Совершает переход
:param matrix: матрица
:return:
"""
temp_matrix = zeros(self.matrix.shape)
for i in range(self.matrix.shape[0]):
for j in range(self.matrix.shape[1]):
temp_matrix[i, j] = sum(
self.matrix[i, m] * matrix[m, j] if m != j else 0
for m in range(self.matrix.shape[0])
)
return temp_matrix
def probability_of_the_first_transition(self, of: int, to: int, n: int) -> float:
"""
Вероятность первого перехода
:param of:
:param to:
:param n:
:return:
"""
temp_matrix = self.matrix
for _ in range(2, n + 1):
temp_matrix = self.make_step_in_matrix(temp_matrix)
return temp_matrix[of - 1, to - 1]
def probability_of_transition_no_later_than(
self, of: int, to: int, n: int
) -> float:
"""
Вероятность перехода не позднее чем
:param of:
:param to:
:param n:
:return:
"""
return sum(
self.probability_of_the_first_transition(of - 1, to - 1, step)
for step in range(1, n + 1)
)
def average_number_of_steps_for_the_transition(self, of: int, to: int) -> float:
"""
Среднее количество шагов для перехода
:param of:
:param to:
:return:
"""
of, to = map(lambda x: x - 1, (of, to))
temp_matrix, count = self.matrix, self.matrix[of, to]
for i in range(2, 1000):
temp_matrix = self.make_step_in_matrix(temp_matrix)
count += i * temp_matrix[of, to]
return count
@lru_cache(maxsize=None)
def probability_of_first_return(self, of: int, n: int) -> float:
"""
Вероятность первого возвращения
:param of:
:param n:
:return:
"""
temp_matrix = zeros(self.matrix.shape)
for i in range(1, n):
temp_matrix += self.probability_of_first_return(of, i) * matrix_power(
self.matrix, n - i
)
return (matrix_power(self.matrix, n) - temp_matrix)[of - 1, of - 1]
def probability_of_return_no_later_than(self, of: int, n: int) -> float:
"""
Вероятность возвращения не позднее чем
:param of:
:param n:
:return:
"""
return sum(
self.probability_of_first_return(of - 1, step) for step in range(1, n + 1)
)
def average_time_of_return(self, of: int) -> float:
"""
Среднее время возвращения
:param of:
:return:
"""
return sum(
i * self.probability_of_first_return(of - 1, i) for i in range(1, 130)
)
def steady_state_probability(self) -> array:
"""
Установившиеся вероятности
:return:
"""
m = self.matrix.T - eye(self.matrix.shape[0])
m[-1, :] = 1
return dot(linalg.inv(m), array([0] * (self.matrix.shape[0] - 1) + [1]))
def main():
markov_process: MarkovProcess = MarkovProcess.read_from_file("matrix.csv")
task_1 = markov_process.probability_of_switching_to_state(4, 5, 7)
print(
f"1. Вероятность того, что за 7 шагов система перейдет из состояния 4 в состояние 1: {task_1}"
)
task_2 = markov_process.probabilities_of_system_states_in_n_steps(
10,
array(
(
0.08,
0.1,
0.13,
0.09,
0.08,
0.01,
0.1,
0.02,
0.12,
0.05,
0.09,
0.05,
0.06,
0.02,
)
),
)
print(
f"2. Вероятности состояний системы спустя 10 шагов с заданными начальными вероятностями: {', '.join(map(str, task_2))}"
)
task_3 = markov_process.probability_of_the_first_transition(3, 6, 7)
print(
f"3. Вероятность первого перехода за 7 шагов из состояния 3 в состояние 6: {task_3}"
)
task_4 = markov_process.probability_of_transition_no_later_than(14, 5, 8)
print(
f"4. Вероятность перехода из состояния 14 в состояние 5 не позднее чем за 8 шагов: {task_4}"
)
task_5 = markov_process.average_number_of_steps_for_the_transition(7, 1)
print(
f"5. Среднее количество шагов для перехода из состояния 7 в состояние 1: {task_5}"
)
task_6 = markov_process.probability_of_first_return(8, 10)
print(f"6. Вероятность первого возвращения в состояние 8 за 10 шагов: {task_6}")
task_7 = markov_process.probability_of_return_no_later_than(1, 9)
print(
f"7. Вероятность возвращения в состояние 1 не позднее чем за 9 шагов {task_7}"
)
task_8 = markov_process.average_time_of_return(10)
print(f"8. Среднее время возвращения в состояние 10 {task_8}")
task_9 = markov_process.steady_state_probability()
print(f"9. Установившиеся вероятности: {', '.join(map(str, task_9))}")
if __name__ == "__main__":
main()Задана система массового обслуживания со следующими характеристиками:
- Интенсивность поступления
λ=45 - Каналов обслуживания
m=5 - Интенсивность обслуживания
μ=12 - Максимальный размер очереди
n=15
Изначально требований в системе нет
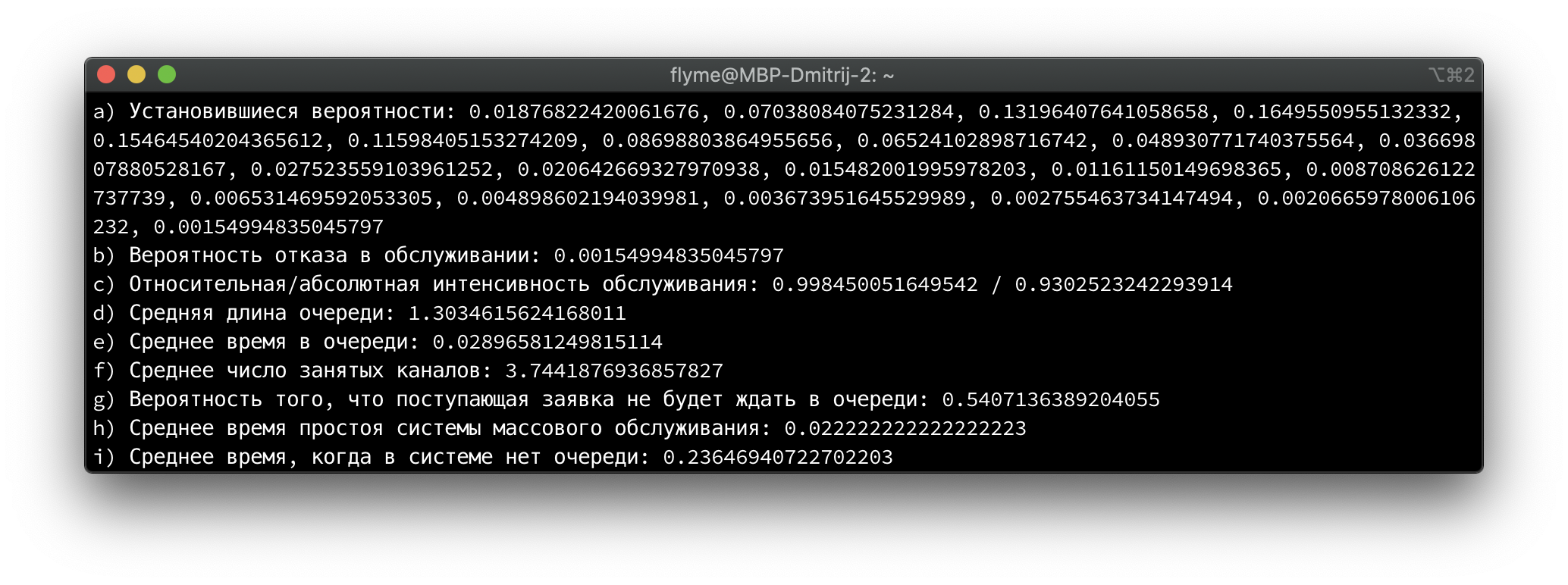
- Составьте граф марковского процесса, запишите систему уравнений Колмогорова и найдите установившиеся вероятности состояний.
- Найдите вероятность отказа в обслуживании.
- Найдите относительную и абсолютную интенсивность обслуживания.
- Найдите среднюю длину в очереди.
- Найдите среднее время в очереди.
- Найдите среднее число занятых каналов.
- Найдите вероятность того, что поступающая заявка не будет ждать в очереди.
- Найти среднее время простоя системы массового обслуживания.
- Найти среднее время, когда в системе нет очереди.
from numpy import array, linalg, zeros, diag, arange, ndarray
class QueueingSystem:
matrix: array
stable_condition: array
def __init__(self, arriving: int, channels: int, intensity: int, max_size: int):
self.arriving = arriving
self.channels = channels
self.intensity = intensity
self.max_size = max_size
self.matrix = self.creation_of_transition_matrix(
arriving, channels, intensity, max_size
)
self.stable_condition = self.establishment_of_the_steady_state_probabilities(
self.matrix
)
@staticmethod
def creation_of_transition_matrix(
arriving: int, channels: int, intensity: int, max_size: int
) -> array:
"""
Создание матрицы переходов
:param arriving:
:param channels:
:param intensity:
:param max_size:
:return:
"""
temp_matrix = zeros((channels + max_size + 1, channels + max_size + 1))
for i in range(channels + max_size):
temp_matrix[i, i + 1], temp_matrix[i + 1, i] = (
arriving,
(intensity * (i + 1) if i < channels else intensity * channels),
)
return temp_matrix
@staticmethod
def establishment_of_the_steady_state_probabilities(matrix: array) -> array:
"""
Установившиеся вероятности
:param matrix:
:return:
"""
new = matrix.T - diag([matrix[i, :].sum() for i in range(matrix.shape[0])])
new[-1, :] = 1
z_m = zeros(new.shape[0])
z_m[-1] = 1
return linalg.inv(new).dot(z_m)
def probability_of_denial_of_service(self) -> float:
"""
Вероятность отказа в обслуживании
:return:
"""
return self.stable_condition[-1]
def bandwidth(self, absolute: bool = False) -> float:
"""
Пропускная способность
:param absolute:
:return:
"""
return (
1 - self.stable_condition[-1] * self.arriving
if absolute
else 1 - self.stable_condition[-1]
)
def average_length_of_the_queue(self) -> float:
"""
Средняя длина очереди
:return:
"""
return sum(
i * self.stable_condition[self.channels + i]
for i in range(1, self.max_size + 1)
)
def average_time_in_the_queue(self) -> float:
"""
Среднее время в очереди
:return:
"""
return sum(
(i + 1)
/ (self.channels * self.intensity)
* self.stable_condition[self.channels + i]
for i in range(self.max_size)
)
def average_number_of_busy_channels(self) -> float:
"""
Среднее число занятых каналов
:return:
"""
return sum(
i * self.stable_condition[i] for i in range(1, self.channels + 1)
) + sum(
self.channels * self.stable_condition[i]
for i in range(self.channels + 1, self.channels + self.max_size + 1)
)
def probability_that_the_incoming_request_will_not_wait_in_the_queue(self) -> float:
"""
Вероятность что поступающая заявка не будет ждать в очереди
:return:
"""
return sum(self.stable_condition[: self.channels])
def average_downtime(self) -> float:
"""
Среднее время простоя
:return:
"""
return 1 / self.arriving
def average_time_when_there_is_no_queue_in_the_system(self) -> float:
"""
Среднее время, когда в системе нет очереди
:return:
"""
probabilities = {i: self.stable_condition[i] for i in range(self.channels + 1)}
normal_coefficient = 1 / sum(probabilities.values())
probabilities = {k: v * normal_coefficient for k, v in probabilities.items()}
return self.time_spent_in_a_subset(
set(probabilities.keys()), probabilities, 0.0005, 10
)
def time_spent_in_a_subset(
self, subset: set, probabilities: dict, time_step: float, time: int
) -> float:
"""
Время пребывания в подмножестве
:param subset: список состояний
:param probabilities: вероятности
:param time_step: шаг времени
:param time: полное время проведения испытаний
:return: время нахождения
"""
temp_matrix = zeros(self.matrix.shape)
for i in subset:
for j in range(self.matrix.shape[0]):
temp_matrix[j][i] = self.matrix[i][j]
for i in subset:
for j in range(self.matrix.shape[0]):
if j != i:
temp_matrix[i][i] -= self.matrix[i][j]
not_subset, f = set(range(self.matrix.shape[0])) - subset, 0
for t in arange(time_step, time + time_step, time_step):
probabilities = self.probability_search(
temp_matrix, subset, probabilities, time_step
)
f += t * sum(
probabilities[i] * self.matrix[i][j] for j in not_subset for i in subset
)
return f * time_step
@staticmethod
def probability_search(
buffer_array: ndarray, subset: set, probabilities: list, time: float
) -> list:
"""
Поиск вероятности
:param buffer_array:
:param subset:
:param probabilities:
:param time:
:return:
"""
coefficients = {x: [0, 0, 0, 0] for x in subset}
for i in subset:
for j in subset:
coefficients[i][0] += buffer_array[i][j] * probabilities[j]
for j in subset:
coefficients[i][1] += (buffer_array[i][j]) * (
probabilities[j] + coefficients[i][0] * time / 2
)
for j in subset:
coefficients[i][2] += (buffer_array[i][j]) * (
probabilities[j] + coefficients[i][1] * time / 2
)
for j in subset:
coefficients[i][3] += (buffer_array[i][j]) * (
probabilities[j] + coefficients[i][2] * time
)
return [
(
probabilities[x]
+ time
* (
coefficients[x][0]
+ 2 * coefficients[x][1]
+ 2 * coefficients[x][2]
+ coefficients[x][3]
)
/ 6
)
for x in subset
]
def main():
queueing_system: QueueingSystem = QueueingSystem(45, 5, 12, 15)
print(
f"a) Установившиеся вероятности: {', '.join(map(str, queueing_system.stable_condition))}"
)
print(
f"b) Вероятность отказа в обслуживании: {queueing_system.probability_of_denial_of_service()}"
)
print(
f"c) Относительная/абсолютная интенсивность обслуживания:"
f" {queueing_system.bandwidth()} / {queueing_system.bandwidth(absolute=True)}"
)
print(f"d) Средняя длина очереди: {queueing_system.average_length_of_the_queue()}")
print(f"e) Среднее время в очереди: {queueing_system.average_time_in_the_queue()}")
print(
f"f) Среднее число занятых каналов: {queueing_system.average_number_of_busy_channels()}"
)
print(
f"g) Вероятность того, что поступающая заявка не будет ждать в очереди:"
f" {queueing_system.probability_that_the_incoming_request_will_not_wait_in_the_queue()} "
)
print(
f"h) Среднее время простоя системы массового обслуживания: {queueing_system.average_downtime()}"
)
print(
f"i) Среднее время, когда в системе нет очереди:"
f" {queueing_system.average_time_when_there_is_no_queue_in_the_system()}"
)
if __name__ == "__main__":
main()