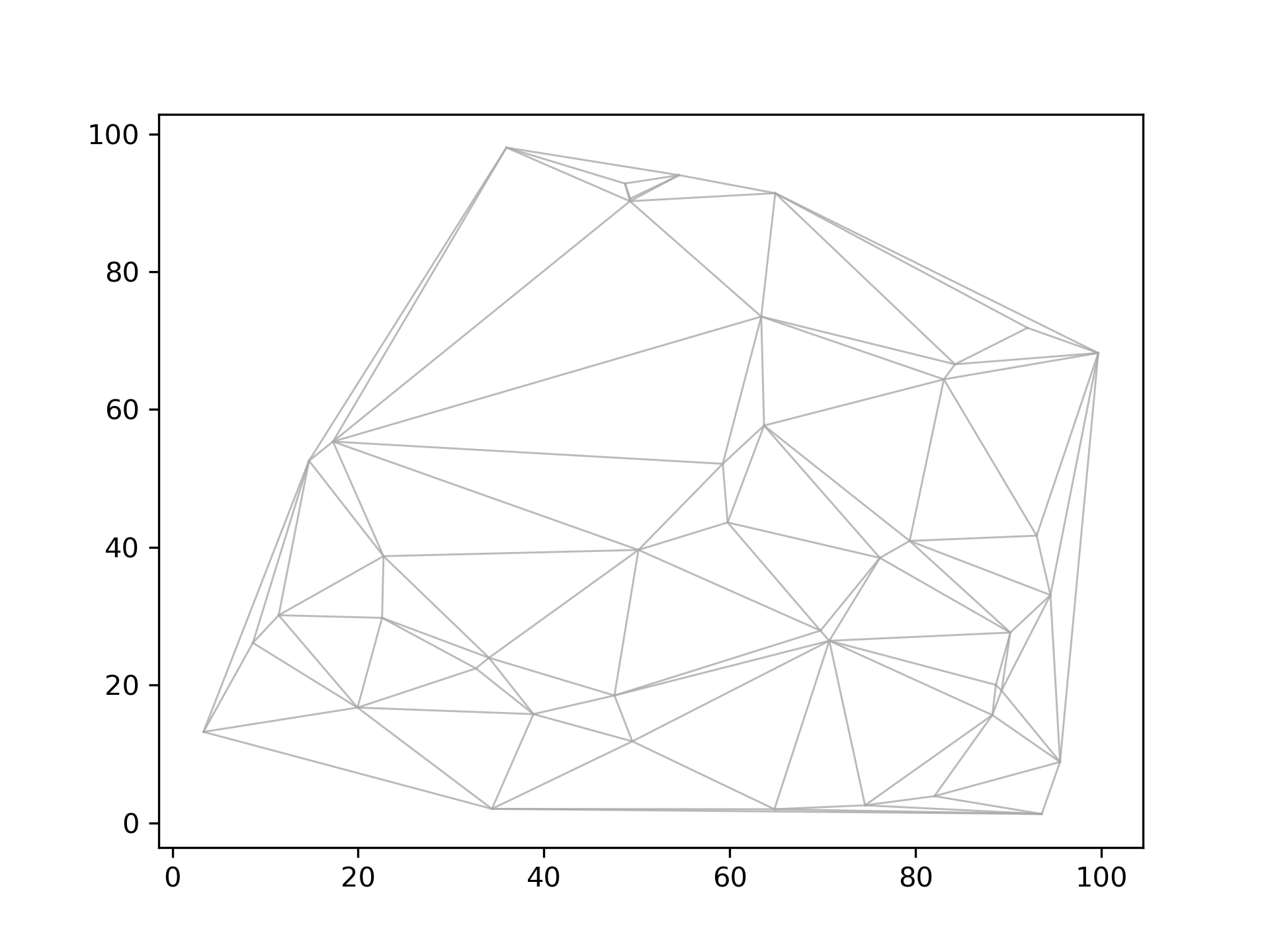
This is a pure python library for finding the delaunay triangulation on given pointsets. Maybe one day voronoi tessellation will be added, since its based on the quad-edge datastructure, which makes finding the dual to each representations easy.
Either clone this repository or install via pip:
pip install delaunay
An example usage looks like this:
from random import seed, uniform
from delaunay.quadedge.mesh import Mesh
from delaunay.quadedge.point import Vertex
from delaunay.delaunay import delaunay
if __name__ == "__main__":
seed(123123123)
N = 44 # number of vertices
vertices = [Vertex(uniform(0, 100), uniform(0, 100)) for v in range(N)]
m = Mesh() # this object holds the edges and vertices
m.loadVertices(vertices)
end = N - 1
delaunay(m, 0, end) # computes the triangulation
# populates a list of [org, dest], values for further manipulation
lines = []
for qe in m.quadEdges:
if qe.org is not None:
lines += [[[qe.org.x, qe.dest.x], [qe.org.y, qe.dest.y]]]
# plotting, for example:
# import matplotlib.pyplot as plt
# fig, ax = plt.subplots()
# for line in lines:
# start, end = line
# ax.plot(start, end)
# plt.show()In their paper 'Primitives for the Manipulation of General Subdivisions and the Computation of Voronoi Diagrams'[0] from 1985, L. Guibas & J. Stolfi propose a divide-and-conquer-algorithm with all the rigor one can hope for. The algorithm runs in O(n log(n)), which should be fine, but for really huge sets R. Dwyers modification [1] of the original algo from 1986 should provide a significant improvement. For now i'll stick with the first one mentioned, but later maybe this work will progress.
In comparison with scipy[2] this library is consirably more lightweight. Of course scipy's delaunay is based on QHull[3], a library written in c, which means it runs ~40 times faster than a python implementation [4].
[0] Guibas, Leonidas and Stolfi, Jorge 'Primitives for the Manipulation of General Subdivisions and the Computation of Voronoi' In: ACM Trans. Graph.4.2 (Apr.1985), pp. 74–123. issn: 0730-0301 doi:10.1145/282918.282923
[1] - Dwyer's Algorithm
[2] - Scipy Delaunay Implementation