From stock prices to climate data, time series data is found in a wide variety of domains, and being able to effectively work with such data is an increasingly important skill for data scientists.
In this lecture, you will be introduced to some common techniques used to import/load, clean and manipulate time series data. Additionally, you'll learn how you can effectively visualize time series data in Python.
You will be able to:
- Load time series data using Pandas and perform time series indexing
- Perform index based slicing to create subsets of a time series
- Change the granularity of a time series
- Perform basic data cleaning operations on time series data
- Explore the temporal structure of time series with line plots
- Understand and describe the distribution of observations using histograms and density plots
- Measure the change in distribution over intervals using box and whisker plots and heat map plots
To get a sense of how to manipulate time series data, we'll walk through an example. The dataset we'll load contains daily minimum temperatures in Melbourne, Australia, from 1981-1990. The data is stored in a .csv-file, so our usual pd.read_csv can be used.
import pandas as pd
temp_data = pd.read_csv("min_temp.csv")
temp_data.head(15).dataframe tbody tr th {
vertical-align: top;
}
.dataframe thead th {
text-align: right;
}
| Date | Daily_min | |
|---|---|---|
| 0 | 1/1/81 | 20.7 |
| 1 | 2/1/81 | 17.9 |
| 2 | 3/1/81 | 18.8 |
| 3 | 4/1/81 | 14.6 |
| 4 | 5/1/81 | 15.8 |
| 5 | 6/1/81 | 15.8 |
| 6 | 7/1/81 | 15.8 |
| 7 | 8/1/81 | 17.4 |
| 8 | 9/1/81 | 21.8 |
| 9 | 10/1/81 | 20.0 |
| 10 | 11/1/81 | 16.2 |
| 11 | 12/1/81 | 13.3 |
| 12 | 13/1/81 | 16.7 |
| 13 | 14/1/81 | 21.5 |
| 14 | 15/1/81 | 25.0 |
Now, let's look at the information of our data set.
temp_data.info()<class 'pandas.core.frame.DataFrame'>
RangeIndex: 3650 entries, 0 to 3649
Data columns (total 2 columns):
Date 3650 non-null object
Daily_min 3650 non-null float64
dtypes: float64(1), object(1)
memory usage: 57.1+ KB
While working with time series data in Python, it's important to always ensure that dates are used as index values and are understood my Python as a true "date" object. This can be done either by using Pandas' Timestamp or base Python’s Datetime and is interchangeable in most cases. It’s the type used for the entries that make up a DatetimeIndex, and other timeseries oriented data structures in pandas. Further details on Timestamp can be found here.
We need to do two things now:
- Make sure that we change the dates in our data sets fron "non-null object" to "non-null datetime". To make sure Python understands the date correctly, a
formatargument can be passed as specified in the documentation. - Make sure that the date becomes the index.
# 1. convert Date to a datetime column
temp_data.Date = pd.to_datetime(temp_data.Date, format='%d/%m/%y')temp_data.info()<class 'pandas.core.frame.DataFrame'>
DatetimeIndex: 3650 entries, 1981-01-01 to 1990-12-31
Data columns (total 1 columns):
Daily_min 3650 non-null float64
dtypes: float64(1)
memory usage: 217.0 KB
3650
# 2. Make Date the index
temp_data.set_index('Date', inplace = True)temp_data.info()<class 'pandas.core.frame.DataFrame'>
DatetimeIndex: 3650 entries, 1981-01-01 to 1990-12-31
Data columns (total 1 columns):
Daily_min 3650 non-null float64
dtypes: float64(1)
memory usage: 57.0 KB
temp_data.head(15).dataframe tbody tr th {
vertical-align: top;
}
.dataframe thead th {
text-align: right;
}
| Daily_min | |
|---|---|
| Date | |
| 1981-01-01 | 20.7 |
| 1981-01-02 | 17.9 |
| 1981-01-03 | 18.8 |
| 1981-01-04 | 14.6 |
| 1981-01-05 | 15.8 |
| 1981-01-06 | 15.8 |
| 1981-01-07 | 15.8 |
| 1981-01-08 | 17.4 |
| 1981-01-09 | 21.8 |
| 1981-01-10 | 20.0 |
| 1981-01-11 | 16.2 |
| 1981-01-12 | 13.3 |
| 1981-01-13 | 16.7 |
| 1981-01-14 | 21.5 |
| 1981-01-15 | 25.0 |
Note how the Date is now the index! Having the date as the index has several advantages, among others, easy visualization with dates on the x-axis, and the functionality to [resample]((http://pandas.pydata.org/pandas-docs/stable/timeseries.html) the data.
Pandas has a simple, powerful, and efficient functionality for performing resampling operations when converting the frequency conversion (e.g., converting monthly data into yearly data). This is very common in financial applications.
temp_monthly= temp_data.resample('MS')
month_mean = temp_monthly.mean()month_mean.head(15).dataframe tbody tr th {
vertical-align: top;
}
.dataframe thead th {
text-align: right;
}
| Daily_min | |
|---|---|
| Date | |
| 1981-01-01 | 17.712903 |
| 1981-02-01 | 17.678571 |
| 1981-03-01 | 13.500000 |
| 1981-04-01 | 12.356667 |
| 1981-05-01 | 9.490323 |
| 1981-06-01 | 7.306667 |
| 1981-07-01 | 7.577419 |
| 1981-08-01 | 7.238710 |
| 1981-09-01 | 10.143333 |
| 1981-10-01 | 10.087097 |
| 1981-11-01 | 11.890000 |
| 1981-12-01 | 13.680645 |
| 1982-01-01 | 16.567742 |
| 1982-02-01 | 15.921429 |
| 1982-03-01 | 14.935484 |
In some cases, it is useful to create upsampled time series as well, especially if you're trying to merge several time series together with different frequencies. You can do this by using "resample" to a time which is more frequent than the timestamp from the original time series.
temp_bidaily= temp_data.resample('12H').asfreq()
temp_bidaily.head().dataframe tbody tr th {
vertical-align: top;
}
.dataframe thead th {
text-align: right;
}
| Daily_min | |
|---|---|
| Date | |
| 1981-01-01 00:00:00 | 20.7 |
| 1981-01-01 12:00:00 | NaN |
| 1981-01-02 00:00:00 | 17.9 |
| 1981-01-02 12:00:00 | NaN |
| 1981-01-03 00:00:00 | 18.8 |
temp_bidaily_fill= temp_data.resample('12H').ffill()
temp_bidaily_fill.head().dataframe tbody tr th {
vertical-align: top;
}
.dataframe thead th {
text-align: right;
}
| Daily_min | |
|---|---|
| Date | |
| 1981-01-01 00:00:00 | 20.7 |
| 1981-01-01 12:00:00 | 20.7 |
| 1981-01-02 00:00:00 | 17.9 |
| 1981-01-02 12:00:00 | 17.9 |
| 1981-01-03 00:00:00 | 18.8 |
Pandas carries the ability to handle date stamp indices allowing quick and handy way of slicing data. For example, we can slice our dataset to only retrieve data points that come after the year 1985.
temp_1985_onwards = temp_data['1985':]
print(temp_1985_onwards.head())
print(temp_1985_onwards.tail()) Daily_min
Date
1985-01-01 13.3
1985-01-02 15.2
1985-01-03 13.1
1985-01-04 12.7
1985-01-05 14.6
Daily_min
Date
1990-12-27 14.0
1990-12-28 13.6
1990-12-29 13.5
1990-12-30 15.7
1990-12-31 13.0
It's pretty common for a time series dataset to have missing values as real world data tends to be messy and imperfect, just like any othe type of data. Simplest way to detect missing values is either plotting the data and identifying disjoint areas of timeseries, or by using DataFrame.isnull() function to get list of all missing values. This function can be used with sum() to get a total count of all missing values.
temp_data.isnull().sum()Daily_min 0
dtype: int64
In this case, there is no missing data. When missingness is present, however, they can be handled in a multitude of ways.
- Drop the data elements with missing values (this may result as low accuracy and loss of valuable information)
- Fill in the missing values under a defined criteria
- Use advanced machine learning methods to predict the missing values
in general, theDataFrame.fillna() function can be used along with, methods like bfill() of ffill() as an argument/criterion for filling in Null values . bfill() (backward filling) looks for the next valid entry in the time series and fills the gaps with this value. Similarly, ffill() can be used to copy forward the previous valid entry of the time series.
Visualizations play an important role in time series analysis. Time series data naturally lends itself to visualization techniques for identifying of rises, falls, trends and noise etc. Plotting raw time series allows data diagnostics to identify certain trends or events.
In what follows, we'll use a data set downloaded from datamarket.com. The data set contains information on the averahe monthly returns of the NYSE between 1961 and 1966.
import pandas as pd
import numpy as np
from pandas.core import datetoolsnyse = pd.read_csv("NYSE_monthly.csv")
col_name= 'Month'
nyse[col_name] = pd.to_datetime(nyse[col_name])
nyse.set_index(col_name, inplace=True)
nyse.head().dataframe tbody tr th {
vertical-align: top;
}
.dataframe thead th {
text-align: right;
}
| monthly_return | |
|---|---|
| Month | |
| 1961-01-01 | 0.082 |
| 1961-02-01 | 0.059 |
| 1961-03-01 | 0.050 |
| 1961-04-01 | 0.008 |
| 1961-05-01 | 0.042 |
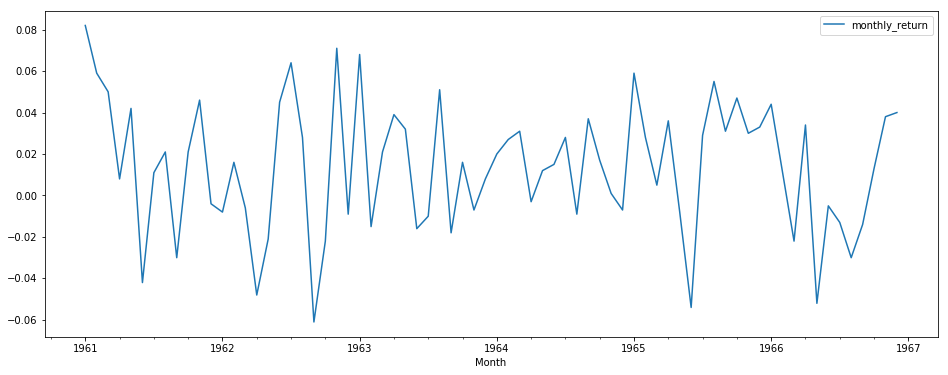
Line plots are the most common technique for visualizing timeseries data as they can clearly show change over time. Using the convention, time is shown on the x-axis with observation values along the y-axis.
Let's use the simple Series.plot() function to draw the line graph for the nyse series.
# Draw a line plot using temp and .plot() function.
nyse.plot(figsize = (16,6))
import matplotlib.pyplot as plt
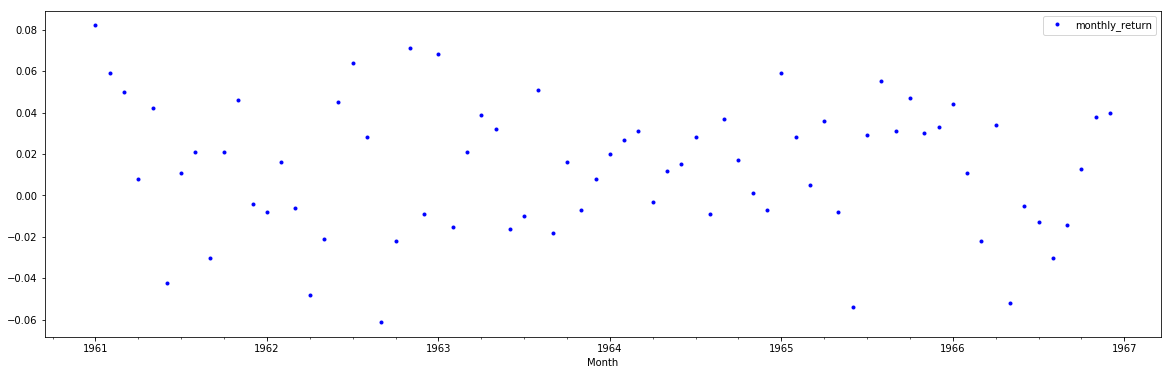
plt.show()For some time series, you may want to change the style of a line plot for a more refined visualization with a higher resolution of events. These time series are not very dense, but
also here it might be useful to change from a continuous line to dots because this representation might be misleading.
You can change the continuous line to dots, each representing one entry in the time series. this can be achieved by style parameter of the line plot. lets pass style='b. as an argument to .plot() function.
# Draw a line plot using temp and .plot() function.
nyse.plot(figsize = (20,6), style = ".b")
import matplotlib.pyplot as plt
plt.show()It's not a surprise to sesee that the general pattern looks very much similar to the line plot, however, we are able to identify some outliers that represent very low and very high return months. Dot plots can prove to be very helpful in identifying outliers and very small patterns which may not be so obvious otherwise.
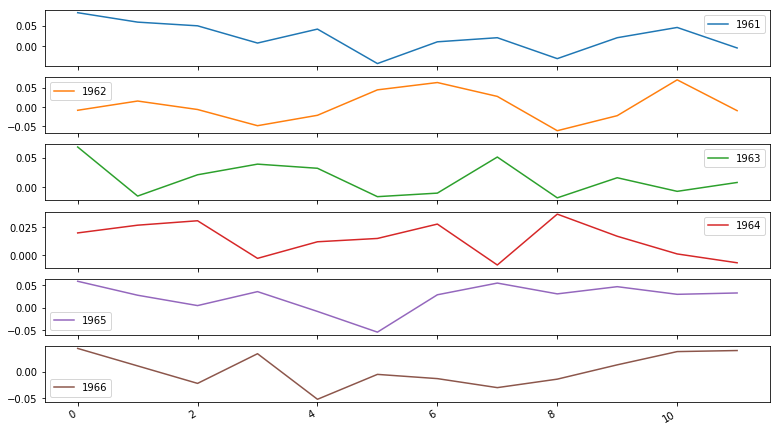
In the dataset, the NYSE returns span 6 years. We can group data by year and create a line plot for each year for direct comparison.
Now, we'll look at how a time series can be regrouped for a given a time interval, i.e. weekly/monthly/yearly average values and compare them to identify any changes taking places over time.
We'll use the Pandas.grouper() method to achieve this. Detailed documentation of this method can be accessed at this location.
- Import pandas grouper and use it to group values by year.
series.groupby(pd.Grouper(freq = ‘A’))
Here, A refers to annual frequency. The list of aliases for time-series frequencies can be found here.
-
Enumerate the groups and observations for each year in a new DataFrame.
-
Plot the DataFrame and visualize each column as a subplot.
# Use pandas grouper to group values using annual frequency
year_groups = nyse.groupby(pd.Grouper(freq ='A'))#Create a new DataFrame and store yearly values in columns
nyse_annual = pd.DataFrame()
for yr, group in year_groups:
nyse_annual[yr.year] = group.values.ravel()
# Plot the yearly groups as subplots
nyse_annual.plot(figsize = (13,8), subplots=True, legend=True)
plt.show()We can see 6 subplots, one for each year. Each plot is 12 months in length following the annual frequency.
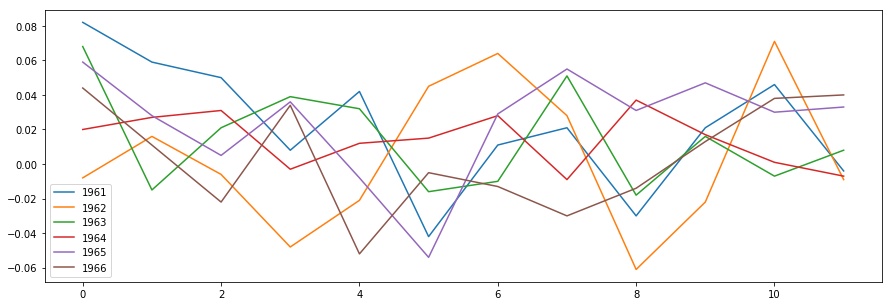
In some cases, it may also be a good a idea to plot these groups in an overlapping manner for a direct comparison. Disabling subplots can help us achieve this.
# Plot overlapping yearly groups
nyse_annual.plot(figsize = (15,5), subplots=False, legend=True)
plt.show()Another important visualization is of the distribution of observations themselves. This means a plot of the values without the temporal ordering.
Most linear time series forecasting methods assume a well-behaved distribution of observations e.g. a normal distribution. This can be explicitly checked using tools like statistical hypothesis tests we saw during hypothesis testing exercises. Visualizing these distributions can provide a useful first check of the distribution of observations both on raw observations and after any type of data transform has been performed.
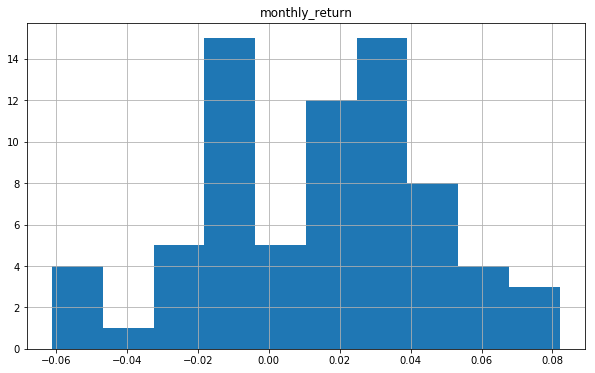
We will now create a histogram plot of the observations in the dataset using hist().
A histogram groups values into bins, and the frequency or count of observations in each bin can provide insight into the underlying distribution of the observations.
nyse.hist(figsize = (10,6))
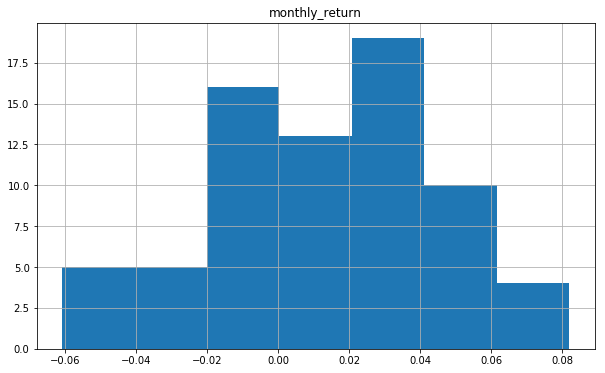
plt.show()The plot shows a distribution that doesn't exactly look Gaussian/Normal. The plotting function automatically selected the size of the bins based on the spread of values in the data here. Let's see what happens if we set the number of bins equal to 7.
nyse.hist(figsize = (10,6), bins = 7)
plt.show()This already looks more normal. With stock exchange returns, it is to be expected that on average, the returns will be 0 and have a gaussian distribution around that. With only 6 years of monthly data, it is to be expected that the distribution does not exactly look gaussian.
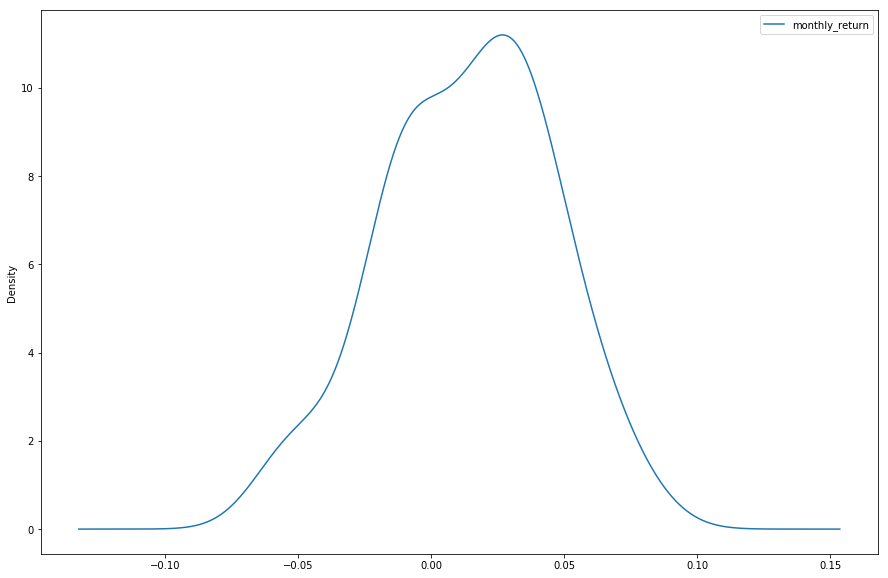
We can also get a better idea of the shape of the distribution of observations by using a density plot which is like the histogram, except a function is used to fit the distribution of observations with smoothing to summarize this distribution.
Let's plot a density plot of the NYSE stock exchange data. We will achieve this by setting the kind parameter of the plot() function to KDE, which stands for Kernel Density Estimation.
# Plot a density plot for temperature dataset
nyse.plot(kind='kde', figsize = (15,10))
plt.show()We can see that density plot provides a clearer summary of the distribution of observations. We can see that perhaps the distribution is more gaussian than we were able to see in the histogram.
Seeing a distribution like this may suggest later exploring statistical hypothesis tests to formally check if the distribution is Gaussian and perhaps data preparation techniques to reshape the distribution.
Histograms and density plots provide insight into the distribution of all observations, but we may be interested in the distribution of values by time interval.
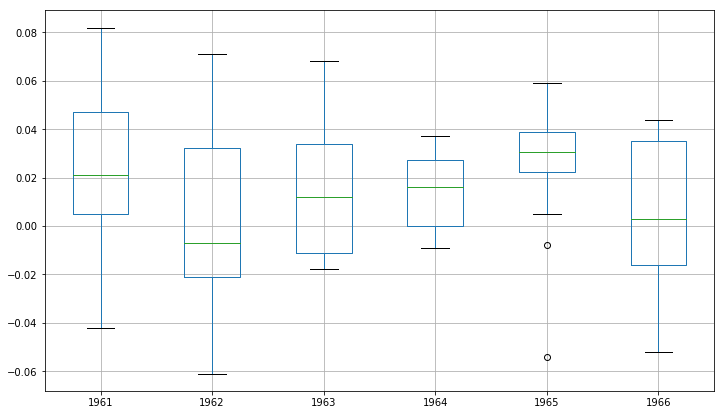
Another type of plot that is useful to summarize the distribution of observations is the box and whisker plot. This plot draws a box around the 25th and 75th percentiles of the data that captures the middle 50% of observations. A line is drawn at the 50th percentile (the median) and whiskers are drawn above and below the box to summarize the general extents of the observations. Dots are drawn for outliers outside the whiskers or extents of the data.
Box and whisker plots can be created and compared for each interval in a time series, such as years, months, or days.
Let's use our groups by years DataFrame to plot a box and whisker plot for each year, side-by-side for direct comparison using boxplot().
# Generate a box and whiskers plot for temp_annual dataframe
nyse_annual.boxplot(figsize = (12,7))
plt.show()Comparing box and whisker plots by consistent intervals is a useful tool. Within an interval, it can help to spot outliers (dots above or below the whiskers).
Across intervals, we can look for multiple year trends, seasonality, and other structural information that could be modeled. Seasonality is generally not a thing in financial data, but in the lab that follows you'll explore visualizing the temperature data!
A matrix of numbers can be plotted as a surface, where the values in each cell of the matrix are assigned a unique color. This is called a heatmap, as larger values can be drawn with warmer colors (yellows and reds) and smaller values can be drawn with cooler colors (blues and greens). Like the box and whisker plots, we can compare observations between intervals using a heat map.
In the case of our NYSE dataset, the observations can be arranged into a matrix of year-columns and month-rows, with monthly returns in the cell for each day. A heat map of this matrix can then be plotted.
We'll now create a heatmap of the Minimum Daily Temperatures data. The matshow() function from the matplotlib library is used as no heatmap support is provided directly in Pandas.
-
Rotate (transpose) the
nyse_annualdataframe as a new matrix the matrix so that each row represents one year and each column one day. This provides a more intuitive, left-to-right layout of the data. -
Use
matshow()function to draw a heatmap for transposed yearly matrix. details on matshow can be accessed here.
year_matrix = nyse_annual.T
plt.matshow(year_matrix, interpolation=None, aspect='auto', cmap=plt.cm.Spectral_r)
plt.show()Orange/red colors represent higher values, blue represents low values, green represents values in the middle. Heatplots will make more sense after you've gone through the lab which will follow later and examinge the Australian temperature data.
An overview of Pandas time series functionality can be found here.
Some more manipulation tricks can be found here.
In this introductory lesson, we learnt how to create a time-series object in Python using Pandas. We learnt to fulfil all the requirements for a dataset to be classified as a time-series by ensuring timestamp values as data index. Basic data handling techniques for getting time-series data ready for further analysis were introduced. We also learnt how to explore the temporal relationships with line, scatter, and autocorrelation plots. We also explored the distribution of observations with histograms and density plots and change in distribution of observations with box and whisker and heat map plots.