Extended version for future reference: https://friendshipkim.notion.site/Implementing-Transformer-from-Scratch-5ec3145047774d5899df2470a73fc94f

Implementing Transformer from Scratch

The goal of this project is to implement a Transformer model from scratch, originally proposed in Attention is all you need paper. Among lots of good implementations, I chose PyTorch transformer - torch.nn.transformer as the baseline. My goal is to replicate the model and machine translation results from this tutorial.

Transformer basics

Given the popularity of the model, I'll only provide a brief description of its architecture. Transformer makes use of the attention mechanism to draw global dependencies between input and output. It can achieve significantly more parallelization than RNN by avoiding recurrence with attention. The skeleton of the model is encoder-decoder architecture. The encoder maps an input sequence into continuous representations, which is also called as memory. The decoder generates an output sequence based on memory.

Model architecture

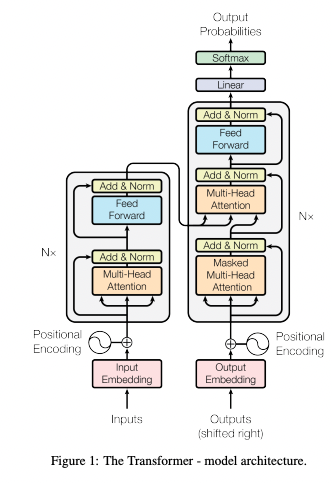
The model architecture is depicted in Figure 1 of the paper. It is divided into four major modules: embedding, encoder, decoder, and final classifier.

Embedding
- Token embedding
- Positional encoding
Encoder - Stack of N identical encoder layers)
- Encoder layer
  - Multi-head self-attention block
  - Feed-forward block
Decoder - Stack of N identical encoder layers)
- Decoder layer
  - Multi-head self-attention block
  - Multi-head cross-attention block
  - Feed-forward block
Final classifier

In terms of implementation, the model has four basic building blocks. Each building block performs the following:

Token embedding - Learned embeddings to convert input and output tokens to vectors with d_model dimensions.
Positional encoding - Indicates the relative or absolute position of the tokens in the sequence, and is added element-wise to token embeddings.
Multi-head attention block - Attention maps a query and a set of key-value pairs to an output. The multi-head attention block is made up of h parallel attention heads. Inputs and outputs for each attention head are d_k = d model / h dimensioned vectors.
Feed-forward block - A fully connected feed-forward network composed of two linear transformations with a ReLU activation in between.

My implementation

In my implementation, the embedding and final classifier are encapsulated in model/transformer.py, while the encoder and decoder are in model/encoder.py and model/decoder.py, respectively. The basic building blocks mentioned above are under model/sublayer/ directory. This is how I organized my model implementation.

model
├── transformer.py
├── encoder.py
├── decoder.py
├── layer
│   ├── encoder_layer.py
│   └── decoder_layer.py
├── sublayer
│   ├── multihead_attention.py
│   ├── ffn_layer.py
│   ├── token_embedding.py
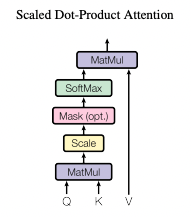
│   └── positional_encoding.py

Scaled dot-product attention

Now, let's take a closer look at scaled dot-product attention, which is at the heart of the transformer model. Scaled dot-product attention takes query, key, and value as inputs. The output is computed as a weighted sum of the values, with the weight determined by the query and key.

My scaled dot-product attention method is under model.sublayer.multihead_attention.MultiheadAttention class. The query is a batch_size * h, q_len, d_k shaped tensor, and the key and value are also batch_sizes * h, k_len, d_k shaped tensors. The query can have different sequence lengths from the other two, but the key and value must have the same length.

The code is as follows:

def calculate_attn(
          self, q: Tensor, k: Tensor, v: Tensor, mask: Tensor = None
  ) -> typing.Tuple[Tensor, Tensor]:
      """
      calculate scaled dot product attention

      :param q: torch.Tensor, shape: (batch_size * h, q_len, d_k)
      :param k: torch.Tensor, shape: (batch_size * h, k_len, d_k)
      :param v: torch.Tensor, shape: (batch_size * h, k_len, d_k)
      :param mask: torch.Tensor, shape: (batch_size * h, q_len, k_len)

      :return attn_out: torch.Tensor, shape: (batch_size * h, q_len, k_len)
      :return attn_score: torch.Tensor, shape: (batch_size * h, q_len, q_len)
      """

      # 1. scaling
      q = q / math.sqrt(self.d_k)

      # 2. QK^T
      attn_score = torch.bmm(q, k.transpose(-2, -1))  # shape: (batch_size * h, q_len, k_len)
      # (3. masking)
      if mask is not None:
          attn_score = attn_score.masked_fill(mask == 0, value=float("-inf"))

      # 4. softmax
      attn_score = F.softmax(attn_score, dim=-1)  # shape: (batch_size * h, q_len, k_len)

      # (dropout)
      # This is actually dropping out entire tokens to attend to, which might
      # seem a bit unusual, but is taken from the original Transformer paper.
      attn_score = self.dropout(attn_score)

      # 5. dot product with V
      attn_out = torch.bmm(attn_score, v)  # shape: (batch_size * h, q_len, d_k)

      return attn_out, attn_score

Baseline implementation

PyTorch transformer is the baseline I want to replicate. torch.nn.modules.transformer module contains all model components except for the embedding layers. It's worth noting that its default configuration is batch_first=False, which means that the input shape is (seq_len, batch_size, d_model), transposing the first and second dimensions of my implementation.

Multihead attention block is torch.nn.activation.MultiheadAttention, but actual forwarding occurs when calling torch.nn.F.multi_head_attention_forward() function. For scaled dot-product attention calculation, torch.nn.F._scaled_dot_attention() function is similar to my calculate_attn() function above.

Model verification

Before training, I needed to make sure that my model has the same forward and backward pass as the baseline. To do so, I created a list of model statistics and check if they are the same for both models.

Checklist

Let’s run the code

Setup

pip install requirements.txt
pip install -e .

Model verification

python ./tests/test_trainsformer.py

Training

Now let’s train two models with the simple machine translation dataset, Multi30K. Adam optimizer is used, with a batch_size of 32, and epochs of 15. All model configurations and training hyperparameters are specified in config.py file.

To train the model:

# train baseline model
python main_mt.py --model-type baseline

# train my model
python main_mt.py --model-type my

Testing

To evaluate and print the test loss of the best model (which has the lowest validation loss):

# test baseline model
python main_mt.py --model-type baseline --evaluate True

# test my model
python main_mt.py --model-type my --evaluate True

Results

Training logs

Baseline model

Epoch: 1, Train loss: 4.4871, Val loss: 3.8039, Epoch time = 52.652s
Epoch: 2, Train loss: 3.6234, Val loss: 3.4906, Epoch time = 52.577s
Epoch: 3, Train loss: 3.3233, Val loss: 3.2913, Epoch time = 52.472s
Epoch: 4, Train loss: 3.0833, Val loss: 3.1061, Epoch time = 52.459s
Epoch: 5, Train loss: 2.8785, Val loss: 2.9594, Epoch time = 52.458s
Epoch: 6, Train loss: 2.6489, Val loss: 2.7452, Epoch time = 52.673s
Epoch: 7, Train loss: 2.3937, Val loss: 2.4923, Epoch time = 52.777s
Epoch: 8, Train loss: 2.1348, Val loss: 2.3153, Epoch time = 61.615s
Epoch: 9, Train loss: 1.9175, Val loss: 2.1903, Epoch time = 52.868s
Epoch: 10, Train loss: 1.7464, Val loss: 2.1355, Epoch time = 53.000s
Epoch: 11, Train loss: 1.6094, Val loss: 2.0798, Epoch time = 52.860s
Epoch: 12, Train loss: 1.4846, Val loss: 2.0489, Epoch time = 52.964s
Epoch: 13, Train loss: 1.3819, Val loss: 2.0300, Epoch time = 52.968s
Epoch: 14, Train loss: 1.2895, Val loss: 2.0113, Epoch time = 53.001s
Epoch: 15, Train loss: 1.2102, Val loss: 2.0424, Epoch time = 52.878s

My model

Epoch: 1, Train loss: 4.4904, Val loss: 3.8435, Epoch time = 56.186s
Epoch: 2, Train loss: 3.6351, Val loss: 3.4986, Epoch time = 56.136s
Epoch: 3, Train loss: 3.3299, Val loss: 3.2877, Epoch time = 55.834s
Epoch: 4, Train loss: 3.0969, Val loss: 3.1456, Epoch time = 55.873s
Epoch: 5, Train loss: 2.8875, Val loss: 2.9348, Epoch time = 55.933s
Epoch: 6, Train loss: 2.6291, Val loss: 2.7235, Epoch time = 55.994s
Epoch: 7, Train loss: 2.3478, Val loss: 2.4603, Epoch time = 55.888s
Epoch: 8, Train loss: 2.0843, Val loss: 2.2771, Epoch time = 56.395s
Epoch: 9, Train loss: 1.8769, Val loss: 2.1647, Epoch time = 56.071s
Epoch: 10, Train loss: 1.7149, Val loss: 2.1116, Epoch time = 56.210s
Epoch: 11, Train loss: 1.5778, Val loss: 2.0779, Epoch time = 56.123s
Epoch: 12, Train loss: 1.4668, Val loss: 2.0500, Epoch time = 56.168s
Epoch: 13, Train loss: 1.3670, Val loss: 2.0396, Epoch time = 60.289s
Epoch: 14, Train loss: 1.2777, Val loss: 2.0254, Epoch time = 73.164s
Epoch: 15, Train loss: 1.1974, Val loss: 2.0281, Epoch time = 62.193s

Training loss trends of the two models are not exactly the same due to nondeterminism in weight initialization and dropout, but they show a similar trend. Nondeterminism can be removed by 1. using custom dropout instead of nn.Dropout, 2. using SGD instead of Adam, and 3. initializing the baseline model first and copying the weights to my model. After nondeterministic properties are removed, the two models have the same training loss trend.

Test loss
- Baseline model
```
Test loss: 2.0176
```
- My model
```
Test loss: 2.0239
```

Future works

Train with larger datasets: IWSLT2016 or 2017
Implement beam search
Measure BLEU score

friendshipkim/transformer-from-scratch

Implementing Transformer from Scratch

Transformer basics

Model architecture

My implementation

Scaled dot-product attention

Baseline implementation

Model verification

Checklist

Let’s run the code

Setup

Model verification

Training

Testing

Results

Future works