/RPSGame

Primary LanguageJavaScriptMIT LicenseMIT

RPSGameVisualization

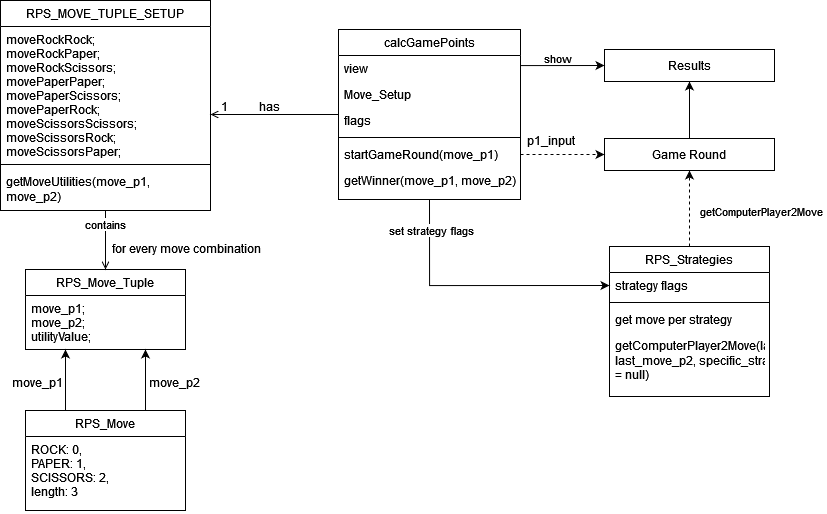
This is a Visualization of the Rock, Paper, Scissors Game showing its connections to Game Theory. It was made by M-Gentes in cooperation with Professor Dr. Oscar Lin.

Learning Objectives of the Rock, Paper, Scissors Game

Introduction

  • You can play Rock, Paper, Scissors against a Computer player (CPU).
  • By default the CPU chooses their move randomally in a equal manner, so one of the three options is choosed one third of the time.
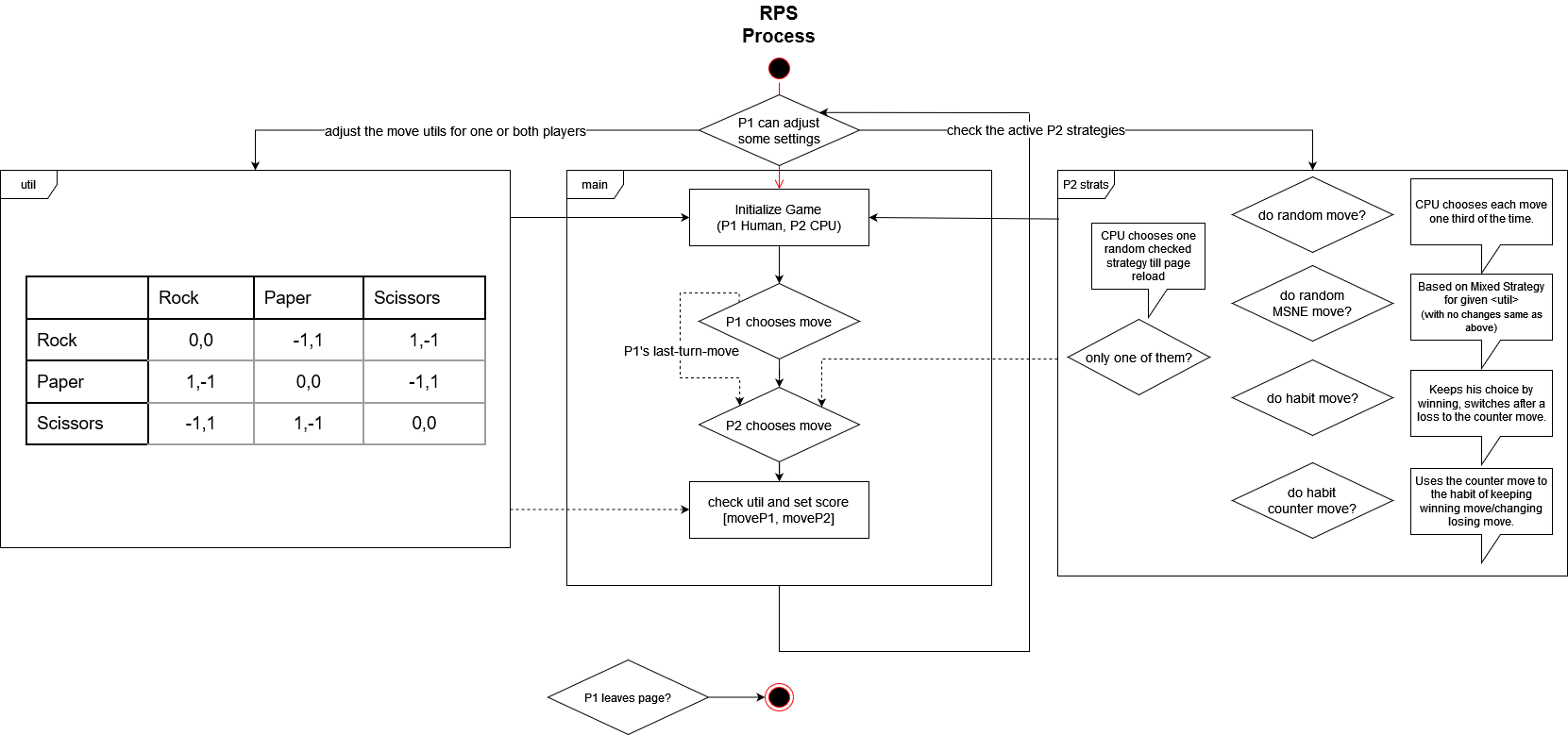
  • But by pressing the Settings button ⚙ in the top bar, there are some settings to change up the game.
  • The area with the checkboxes determines the behavior of the CPU agent. So for each checked strategy, the CPU chooses randomally one of his strategies (based on a uniform distribution probability).
    • By default the CPU chooses each round one of his strategies, but if Opponent uses only one of the checked Strategies is checked, it chooses one of his strategies for the hole game.
  • With the Utility table below you can change the utility values for the tuple of options used, so [Rock,Paper] could result in a different score as [-1,1] respectively for each player.
    • The rows show the options for player 1 (real person) and the columns show the options for player 2 (CPU).

Strategies

  • The strategies for the CPU are the following:
    • Opponent uses random move: CPU chooses each move one third of the time.
    • Opponent uses his Mixed Strategy Nash Equilibria: CPU chooses each move based on the given utility for the RPS tuples used (without changing the utilities it results to the same as the previous strategy).
    • Opponent uses his moves in a certain habit: CPU uses the same move of the last round if it won, if it lost it uses the counter move to the move it was using. After a tie it chooses a random move.
    • Opponent tries to counter common habit moves: CPU tries to counter the previous strategy. If the real player has the habit of the previous strategy, the CPU will be winning all the time (except after ties).

MSNE

The Expected Utilities (using the move Left (Rock), Center (Paper) or Right (Scissors) - as seen in the utility table) for player 2 (CPU) can be put together to an linear equation system and with that you can calculate the probabilities for the Mixed Strategy Nash equilibria. By restructuring the equations with some substitutions let them be calculated in base Javascript:

$$EUU = EUM = EUD$$ $$EUU = dL a2 + dC d2 + (1-dL-dC) g2$$ $$EUM = dL b2 + dC e2 + (1-dL-dC) h2$$ $$EUD = dL c2 + dC f2 + (1-dL-dC) i2$$

$\implies$

$$x = {(-d2+e2+g2-h2) \over (a2-b2-g2+h2)}$$ $$y = {(h2-g2) \over (a2-b2-g2+h2)}$$ $$p = -b2 + h2 + c2 - i2$$ $$q = -h2 + i2$$
  • Restructure to get sigma probability variables
$$dC = {((y) p + q) \over ((-x) p + q + e2 - f2)}$$ $$dL = dC (x) + (y)$$ $$dR = 1 - dC - dL$$
  • see the Game Theory 101 video series for more information, which was used as a basis

Images

  • RPS process diagramm

    • RPS process diagramm

  • RPS code diagramm

    • RPS code diagramm

Credits

Sounds of Freesound.org were used on this application.

  • "Stone.wav" by danielpodlovics of Freesound.org
  • "Book, Flipping Through Pages, A.wav" by InspectorJ (www.jshaw.co.uk) of Freesound.org
  • "Scissors.wav" by Godowan of Freesound.org
  • "metallic_cling1.mp3" by ZorroBms1001 of Freesound.org