To quote Alvin Roth and Lloyd Shapley, matching is "one of the important functions of markets. Who get which jobs, which school places, who marries whom, these help shape lives and careers".
This is a solved two-side matching problem, and Alvin Roth and Llyod Shapley were awarded the Nobel Memorial Prize in Economic Science in 2012 for their Deferred Acceptance Algorithm (proved in 1962). This paper can be found here, for those interested in the economics and mathematics. https://web.stanford.edu/~alroth/papers/GaleandShapley.revised.IJGT.pdf
In my Python implementation, I'll first share:
-
- the classic one-to-one scenario, and then extend it to
-
- many-to-many scenario (more complex)
To help you understand the scenarios conceptually, the one-to-one scenario as monogamy and many-to-many as polygamy.
The algorithm is very elegant, with proven stability (an economic property). Assuming a stable matching exists, the solutions are not unique. Therefore you can re-run it to return another valid matching. The results depend on which Suitor proposes first (fix the random seed if you need reproducibility).
Moreover, you can generalize the code to any matching problem with two-sided parties with ranking preferences, and capacity limits. (e.g. medical resident matching, matching for co-op jobs, marriage - although it probably isn't really practical in that last one)
Lastly, I've incorporated scripts to take matching results, transfer them into a schedule format, and then also optimize for any conflicts.
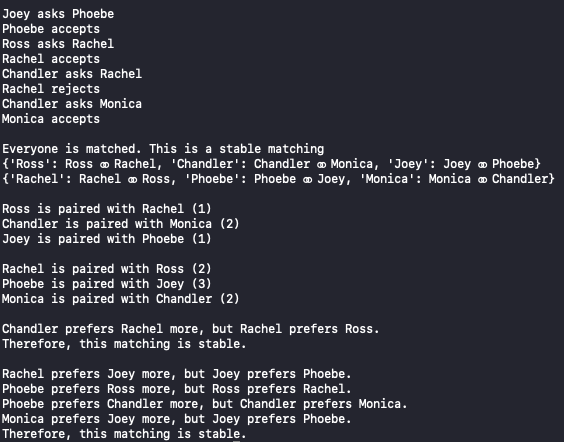
See overview.pdf to familiarise yourself with the setup with an example of a one-to-one example (using your favourite cast members of Friends). Special shoutout to maxhumber for inspiring this.
cd into the directory and run in the Terminal
$ python matching_1_to_1.py
The following are the scripts to run the Deferred Acceptance Algorithm (DAA) software. The terminology I'll use is Suitors and Suited for the two parties. (In practice, it would be students/hospitals, interviewees/employers, men/women etc.)
step_0_data_sim.py
Run this script to simulate data for 1) Suitor rankings and 2) Suited rankings.
- Change the assumptions of the sampling distributions. For the data I was simulating, I sampled from a geometric and uniform distribution.
- Set the number of Suitors and Suited, and their capacity.
step_1_daa_many_to_many.py
Run this script to run the DAA and produce a matching csv file (and optional reports to explain the results).
step_2_test_marriage.py
Run this script to run test cases. If you make any changes to step_1_daa_many_to_many, then run this script for regression tests.
step_3_mini_sheet.py
(Optional) Run this script to generate a schedule and minimize any conflicts. This is the output file.
Sim_pipeline.py
(Optional) Run this pipeline script to simulate results. It tests the software by calculating the proportion of solutions that were 1) stable and could be transformed into a 2) perfect schedule (i.e. no conflicts).
With these results, we can understand the edge cases of when Suitors or Suited do not get paired.