Python_Benchmark_Test_Optimization_Function_Single_Objective

Here a repository where you can find and easy access python implementation of a benchmark of functions to challenge single objective optimizations. You can download or fork the repository freely. If you see a mistake you can send me a mail at axel.arcueil@gmail.com or contact me on LinkedIn.

Available functions documentation

You can find the full documentation on this article

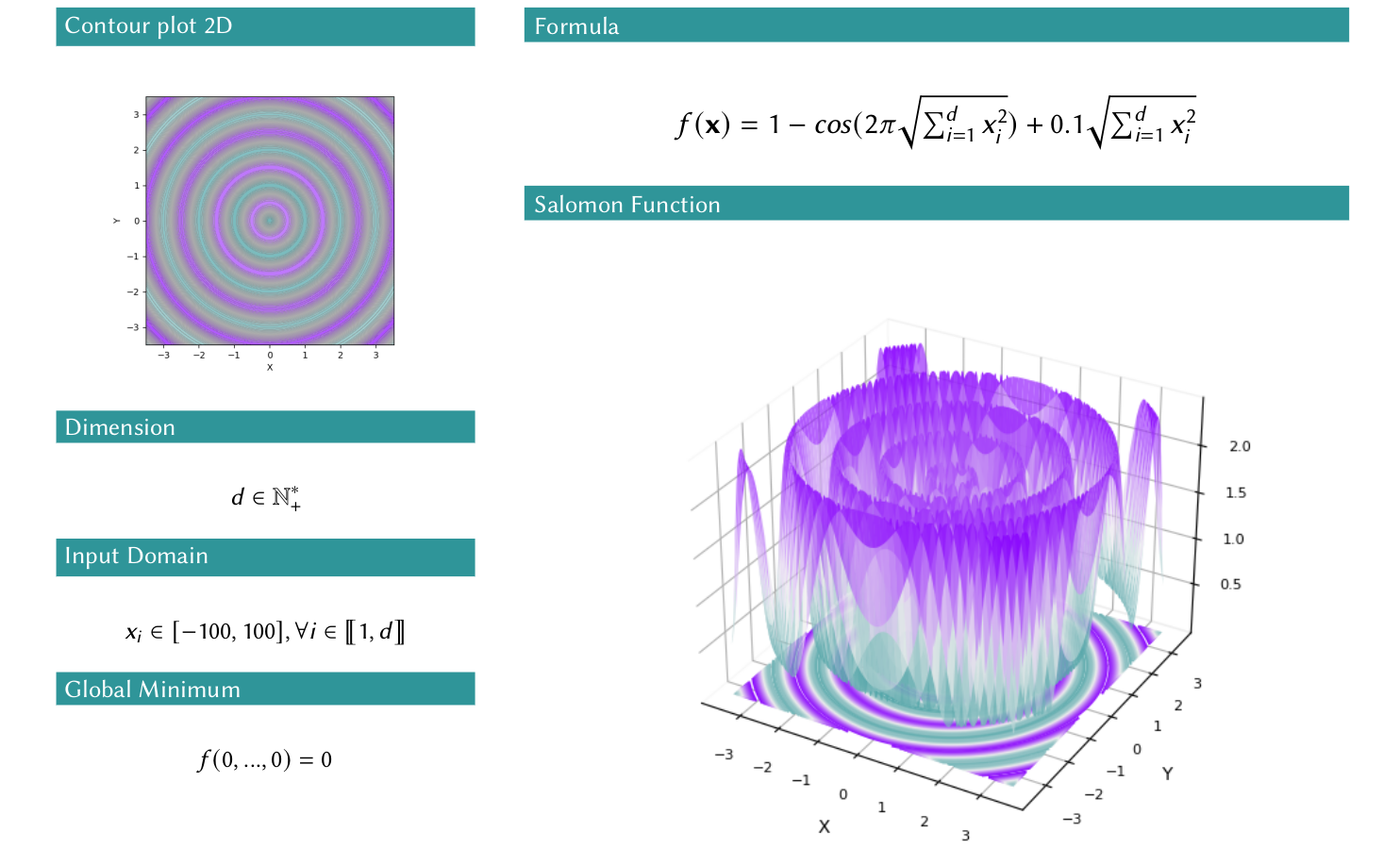
All the functions are describe as you can see on the image above.

Ackley Function
Ackley N. 2 Function
Ackley N. 3 Function
Ackley N. 4 Function
Adjiman Function
Alpine N. 1 Function
Alpine N. 2 Function
Bartels Conn Function
Beale Function
Bird Function
Bohachevsky N. 1 Function
Bohachevsky N. 2 Function
Bohachevsky N. 3 Function
Booth Function
Branin Function
Brent Function
Brown Function
Bukin N. 6 Function
Cross-in-Tray Function
Colville Function
De Jong N. 5 Function
Deckkers-Aarts Function
Dixon-Price Function
Drop-Wave Function
Easom Function
Egg Crate Function
Eggholder function
Exponential Function
Forrester Function
Goldstein-Price Function
Gramacy & Lee Function
Griewank Function
Happy Cat Function
Himmelblau Function
Holder-Table Function
Keane Function
Langermann Function
Leon Function
Levy N. 13 Function
Matyas Function
McCormick Function
Michalewicz Function
Periodic Function
Perm Function 0, d, β
Perm Function d, β
Powell Function
Qing Function
Quartic Function
Rastrigin Function
Ridge Function
Rosenbrock Function
Rotated Hyper-Ellipsoid Function
Salomon Function
Schaffer N. 1 Function
Schaffer N. 2 Function
Schaffer N. 3 Function
Schaffer N. 4 Function
Schwefel Function
Schwefel 2.20 Function
Schwefel 2.21 Function
Schwefel 2.22 Function
Schwefel 2.23 Function
Shekel Function
Shubert Function
Shubert N. 3 Function
Shubert N. 4 Function
Six-Hump Camel Function
Sphere Function
Styblinski-Tank Function
Sum Squares Function
Three-Hump Camel Function
Thevenot Function
Trid Function
Wolfe Function
Xin-She Yang Function
Xin-She Yang N. 2 Function
Xin-She Yang N. 3 Function
Xin-She Yang N. 4 Function
Zakharov Function

Easy Use

One-liner access: Filter the functions with their characteristics

import pybenchfunction as bench
# get all the available functions accepting ANY dimension
any_dim_functions = bench.get_functions(None)
# get all the available continuous and non-convex functions accepting 2D
continous_nonconvex_2d_functions = bench.get_functions(
    2,  # dimension
    continuous=True,
    convex=False,
    separable=None,
    differentiable=None,
    mutimodal=None,
    randomized_term=None
)
print(len(any_dim_functions))  # --> 40
print(len(continous_nonconvex_2d_functions))  # --> 41

Import specific function

# set the dimension of the input for the function
sphere = bench.function.Sphere(3)
# get results
X = np.array([1, 3, 0])
print(sphere(X))  # --> 10

Plot 2d or plot 3d contours

# Warning ! Only working on 2d functions objects !
# Warning 2! change n_space to reduce the computing time
thevenot = bench.function.Thevenot(2)
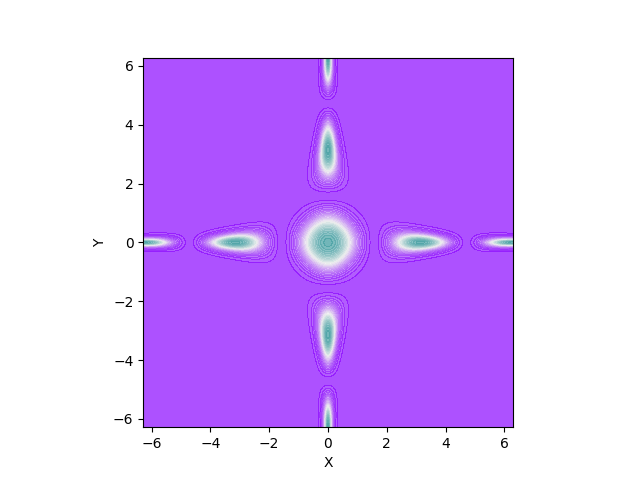
bench.plot_2d(thevenot, n_space=1000, ax=None)
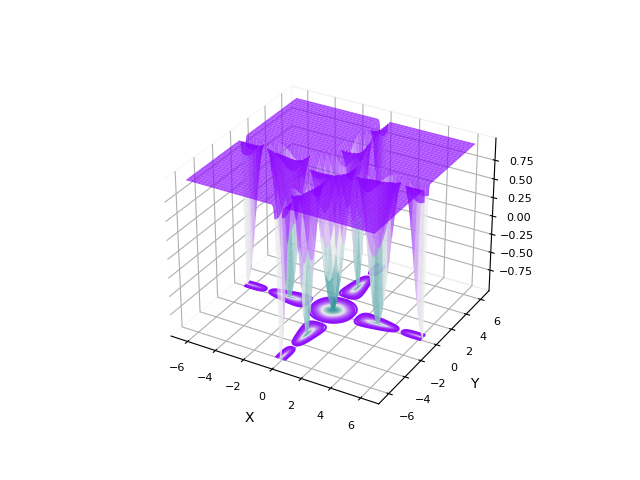
bench.plot_3d(thevenot, n_space=1000, ax=None)

Access/change the parameters of parametrics functions

print(thevenot.get_param())  # --> {'m': 5, 'beta': 15}
thevenot.beta = 42
print(thevenot.get_param())  # --> {'m': 5, 'beta': 42}

Get the global minimum for a specific dimension

X_min, minimum = sphere.get_global_minimum(3)
print(X_min)  # --> [0 0 0]
print(minimum)  # --> 0

Acces/plot the latex formulas

latex = bench.function.Thevenot.latex_formula
# latex = bench.function.Thevenot.latex_formula_dimension
# latex = bench.function.Thevenot.latex_formula_input_domain
# latex = bench.function.Thevenot.latex_formula_global_minimum
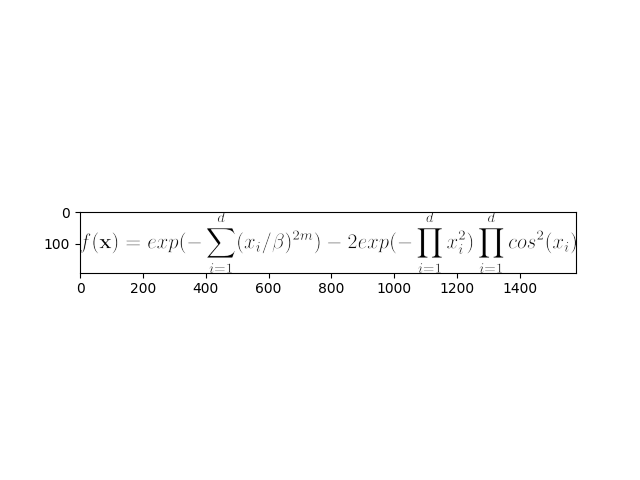
print(latex)  # --> f(\mathbf{x}) = exp(-\sum_{i=1}^{d}(x_i / \beta)^{2m}) - 2exp(-\prod_{i=1}^{d}x_i^2) \prod_{i=1}^{d}cos^ 2(x_i)
latex_img = bench.latex_img(latex)
# convert the latex formula to image
plt.imshow(latex_img)
plt.show()

Uniform implementation

All the functions are Classes implemented in the same way. Here the Sphere example:

class Sphere:
    name = 'Sphere'
    latex_formula = r'f(\mathbf{x})=\sum_{i=1}^{d} x_i^{2}'
    latex_formula_dimension = r'd \in \mathbb{N}_{+}^{*}'
    latex_formula_input_domain = r'x_i \in [-5.12, 5.12], \forall i \in \llbracket 1, d\rrbracket'
    latex_formula_global_minimum = r'f(0, ..., 0)=0'
    continuous = True
    convex = True
    separable = True
    differentiable = False
    mutimodal = False
    randomized_term = False
    parametric = False

    @classmethod
    def is_dim_compatible(cls, d):
        assert (d is None) or (isinstance(d, int) and (not d < 0)), "The dimension d must be None or a positive integer"
        return  (d is None) or (d  > 0)

    def __init__(self, d,):
        self.d = d
        self.input_domain = np.array([[-5.12, 5.12] for _ in range(d)])

    def get_param(self):
        return {}

    def get_global_minimum(self, d):
        X = np.array([0 for _ in range(d)])
        return (X, self(X))

    def __call__(self, X):
        d = X.shape[0]
        res = np.sum(X**2)
        return res

gbelouze/Python_Benchmark_Test_Optimization_Function_Single_Objective