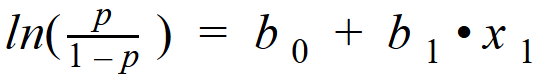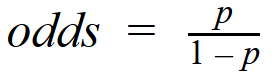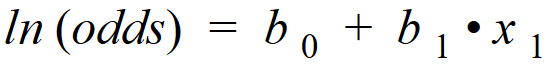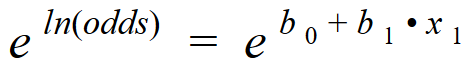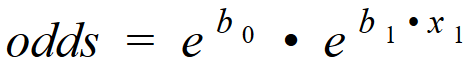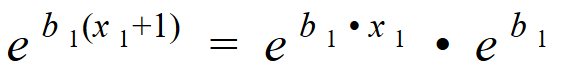Creating a Geosegmentation model to examine bank churn

A geosegmentation model examining the churn of bank customers using logistic regression, variance inflaction factors, and odds ratios with Gretl.

The Variables

RowNumber - This column does not affect a persons decision
CustomerID - A customers ID also does not affect their decision
Surname - Surname is not a deciding factor either
CreditScore - A customers credit score can affect their decision
Geography - Regional data for where the customers are located
- Germany
- France
- Spain
Gender - The gender of a customer may play a role in whether they stay or leave
- Male
- Female
Age - The age of a customer
Tenure - The duration of a customers dealings with a bank - a longer tenure may build loyalty
Balance - A customers bank balance - could affect promotions, interest rates, and account fees
NumOfProducts - How many products a customer subscribes to - more products may lead to higher chances of staying
HasCrCard - If a customer has a credit card with the bank or not - increases the banks presence in a customers life
IsActiveMember - Customers activity with bank in the last 6 months - active customers could be more likely to stay
EstimatedSalary - Banks estimate of a customers salary - higher earners may have more investments with the bank
Exited - Whether a customers stays with the bank or leaves

Exited is the dependent variable as its the outcome of interest and this case study examines the factors that may be associated with a person leaving or staying at the bank. Dummy variables were created for gender and geography with male and France being the baselines respectively. This is so that only a single regression model has to be created.

Variables such as RowNumber, CustomerID, and Surname do not affect whether a person stays or leaves the bank and therefore these columns are not used. The remaining variables will be the regressors.

Modeling the data

Running the first regression iteration results in the following coefficients and p-values:

variables	coefficients	p-values
const	−3.92076	1.76e-057	***
CreditScore	−0.000668329	0.0171	**
Age	0.0727060	2.52e-175	***
Tenure	−0.0159491	0.0882	*
Balance	2.63707e-06	2.92e-07	***
NumOfProducts	−0.101523	0.0312	**
HasCrCard	−0.0446764	0.4515
IsActiveMember	−1.07544	1.43e-077	***
EstimatedSalary	4.80699e-07	0.3102
Female	0.528483	3.04e-022	***
Germany	0.774714	2.41e-030	***
Spain	0.0352178	0.6181

R-squared	Adjusted R-squared	Accuracy (correct predictions)
0.153161	0.150787	8103 (81.0%)

It can be seen that the highest p-value was for Spain, which indicates that it is not a significant variable, therefore we can exclude Spain from the model. When modeling the data again without Spain, the accuracy does not increase and the R-squared value increases very slightly.

variables	coefficients	p-values
const	−3.91097	1.41e-057	***
CreditScore	−0.000666615	0.0174	**
Age	0.0727230	2.00e-175	***
Tenure	−0.0159766	0.0876	*
Balance	2.63733e-06	2.91e-07	***
NumOfProducts	−0.101288	0.0316	**
HasCrCard	−0.0449303	0.4489
IsActiveMember	−1.07519	1.53e-077	***
EstimatedSalary	4.81342e-07	0.3095
Female	0.528343	3.11e-022	***
Germany	0.762937	2.16e-033	***

R-squared	Adjusted R-squared	Accuracy (correct predictions)
0.153137	0.150961	8100 (81.0%)

HasCrCard and EstimatedSalary are removed as these variables have the next highest p-values (above 0.05). After running the model again without these two variables there is a slight increase in accuracy and R-squared score. Now the model shows no variables with a p-value above the threshold.

variables	coefficients	p-values
const	−3.89591	2.31e-061	***
CreditScore	−0.000666426	0.0174	**
Age	0.0727016	2.01e-175	***
Tenure	−0.0159836	0.0873	*
Balance	2.65326e-06	2.44e-07	***
NumOfProducts	−0.100475	0.0330	**
IsActiveMember	−1.07509	1.41e-077	***
Female	0.528981	2.74e-022	***
Germany	0.762059	2.43e-033	***

R-squared	Adjusted R-squared	Accuracy (correct predictions)
0.152978	0.151197	8115 (81.2%)

Log transformation - Balance

Since balance has a large range and a one unit increase from 1000$ to 2000$ shows a doubling effect while a unit increase from 10,000$ to 11,000$ is only a 10% increase, we need to adjust the values so they scale. To do this the log will be taken and 1 will be added to each row in case there's a 0 balance.

This is done in Gretl by defining a new variable and entering the equation log10(balance + 1). The following are the results with replacing balance with log_Balance:

variables	coefficients	p-values
const	−3.91258	3.84e-061	***
CreditScore	−0.000674866	0.0160	**
Age	0.0726550	3.24e-175	***
NumOfProducts	−0.0950198	0.0456	**
IsActiveMember	−1.07578	1.01e-077	***
Female	0.526721	3.97e-022	***
Germany	0.747595	1.44e-030	***
Tenure	−0.0158791	0.0893	*
Log_balance	0.0690263	7.62e-07	***

R-squared	Adjusted R-squared	Accuracy (correct predictions)
0.152787	0.151006	8127 (81.3%)

Derived variable - Wealth_Accumulation

A derived variable may represent some fields such as balance and age more accurately. For example, younger people may have smaller balances and older people may have larger balances that grow with age. Alternatively, a young person may have a lucrative job and have a larger balance compared to an older person who may have lost their savings. This metric may better represent the financial position of customers.

To create this derived variable, the log balance in a bank account can be divided by the age of the account holder. This variable is termed Wealth_Accumulation. The following results are obtained with Wealth_Accumulation as a part of the equation:

variable	coefficients	p-values
const	−3.82758	1.18e-053	***
CreditScore	−0.000675560	0.0160	**
Age	0.0706681	2.00e-115	***
NumOfProducts	−0.0955301	0.0446	**
IsActiveMember	−1.07339	2.57e-077	***
Female	0.525712	4.88e-022	***
Germany	0.746337	2.13e-030	***
Tenure	−0.0159252	0.0884	*
Log_balance	0.0950938	0.0004	***
Wealth_Accumulation	−4.33552e-05	0.2512

R-squared	Adjusted R-squared	Accuracy (correct predictions)
0.152918	0.150940	8123 (81.2%)

Dealing with multicollinearity

Having Wealth_Accumulation, Log_Balance, and age in the model may show a decrease in accuracy and a high p value as there is likely multicollinearity. Gretl can check for collinearity and the variance inflation factor (VIF). The VIF for Log_balance and Wealth_Accumulation are much higher than the other variables.

Variables	VIF
CreditScore	1.001
Age	1.450
NumOfProducts	1.152
IsActiveMember	1.011
Female	1.003
Germany	1.271
Tenure	1.001
Log_Balance	5.860
Wealth_Accumulation	5.722

When taking out Log_Balance, the coefficient for Wealth_Accumulation deflates.

Variables	VIF
CreditScore	1.001
Age	1.115
NumOfProducts	1.118
IsActiveMember	1.011
Female	1.003
Germany	1.187
Tenure	1.001
Wealth_Accumulation	1.387

The metrics for the model containing only Wealth_Accumulation are:

R-squared	Adjusted R-squared	Accuracy (correct predictions)
0.151650	0.149869	8121 (81.2%)

Taking the log of Wealth_Accumulation may possibly be a better metric than the non-transformed variable. Including both Log_Balance and Log_Wealth_Accumulation shows the effects of collinearity with both VIF scores being ~700.

This collinearity effect can be further seen by taking the log of Wealth_Accumulation and including it in the equation along side Log_Balance:

Variables	VIF
CreditScore	1.001
Age	2.265
NumOfProducts	1.152
IsActiveMember	1.012
Female	1.003
Germany	1.270
Tenure	1.002
Log_Wealth_Acccumulation	704.740
Log_Balance	705.941

The metrics for the model containing both the Log_Balance and Log_Wealth_Accumulation variables are:

R-squared	Adjusted R-squared	Accuracy (correct predictions)
0.153511	0.151533	8125 (81.3%)

When assessing performance with only Log_Wealth_Accumulation the metrics are:

R-squared	Adjusted R-squared	Accuracy (correct predictions)
0.152658	0.150878	8128 (81.3%)

Finalizing a model

When comparing the two models where one uses only Log_Wealth_Accumulation and the other only Log_Balance, the model with Log_Balance results in the higher R-squared score (0.151006) and an accuracy only one correct prediction short of the Log_Wealth_Accumulation accuracy (8127 vs 8128).

Which variables have the most impact?

In order to determine which variables are the most important in determining the banks churn rates, the odds ratios for each coefficient need to be calculated.

Calculating the odds ratio

The equation for simple logistic regression:

The odds equation:

Subbing odds into the logistic regression equation (also known as log odds):

Take the exponent of each side:

Simplified:

Increasing a variable by one unit:

The exponents show that an increase of one unit leads to a multiplicative effect:

Conclusion

These ratios can be calculated in Gretl using the function package "odds ratios":

Variables	Odds-ratio
CreditScore	0.9993
Age	1.0754
Tenure	0.9842
NumOfProducts	0.9094
IsActiveMember	0.3410
Female	1.6934
Germany	2.1119
Log_Balance	1.0715

The results show that the most impactful variables are being German, female, and being an active member. The odds-ratio in this case is looking at which factors contribute to a customer leaving. Therefore, when looking at this bank's churn, a customer living in Germany or moving there increases their odds of leaving by a factor of 2.1119. Further, a customer being a female increases their odds of leaving by a factor of 1.6934. Being an active member on the other hand is indicative of a customer staying with the bank. Ultimately, if the bank would like to reduce churn and retain their customer base they would have to target their German customers - especially German females - and work on increasing these customer's activity with the bank.

gdeol4/Geosegmentation_model