Maximum-flow problem

This project represents and solves Maximum-flow problem using the famous Ford-Fulkerson method. The repository contains codes for Graph data structure and it's supports. Graph represented using AdjacencyList, below I leave some literature for those who is interested.

Getting Started

These instructions will get you a copy of the project up and running on your local machine for development and testing purposes.

Prerequisites

This project requires the following to be installed in your local machine:

Windows 8/8.1/10
Microsoft Visual Studio 2017 or upper
Of course, there is a way to run this thing on Linux and Mac without Microsoft VS, but I don't know how :)

Installing

Just clone or download the repository and then open it as a Microsoft VS 2017 project.

Usage

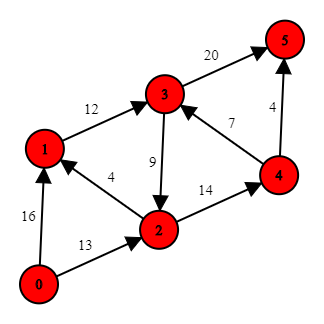
Create a graph

The following piece of code will initialize an oriented weighted graph with 6 vertices:

Graph graph = Graph(6);

graph.addEdge(0, 1, 16);
graph.addEdge(1, 3, 12);
graph.addEdge(3, 5, 20);
graph.addEdge(0, 2, 13);
graph.addEdge(2, 4, 14);
graph.addEdge(4, 5, 4);
graph.addEdge(2, 1, 4);
graph.addEdge(3, 2, 9);
graph.addEdge(4, 3, 7);

Execute The Ford-Fulkerson method

Initialize a new graph.
Initialize a new flow by calling initializeFlow method.
Add some edges (possibly inside some try/catch block).
Call FordFulkersonAlgorithm method in order to calculate the value of the maximum-flow for the given graph.

Graph graph = Graph(6);
graph.initializeFlow();

try {
  graph.addEdge(0, 1, 16);
  graph.addEdge(1, 3, 12);
  // ...
}
catch (const exception& exception) {
  cout << exception.what() << endl;
  return 0;
}

int maxFlow = graph.FordFulkersonAlgorithm();

Running the tests

The project doesn't have any test yet.

Authors

See the list of contributors who participated in this project.

License

This project is licensed under the MIT License - see the LICENSE.md file for details

Literature

[1] Ford, L. R., Jr., Fulkerson, D. R. (1962). Flows in Networks. Princeton, NJ.

[2] Cormen, T.H., Leiserson, C. E., Rivest, R. L. (2009). Introduction to Algorithms, 3rd Edition.

[3] Hemant, J. (2016). Problem Solving in Data Structures & Algorithms Using C++, First Edition.