Lotka-Volterra competition model in Stan

Data

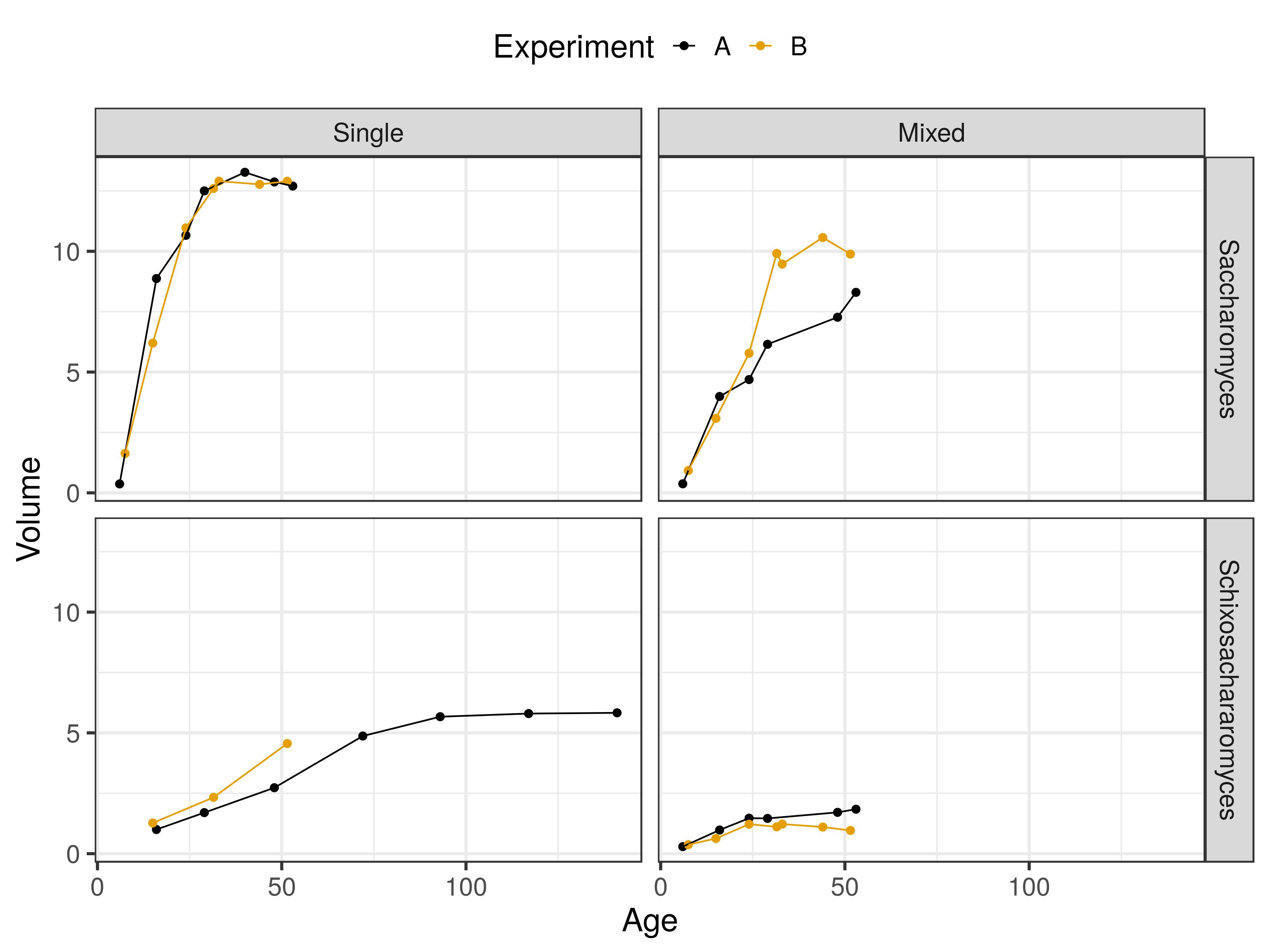
The data is available in two csv files in the Data folder (one for each set of experiment) and was published in Gause (1932) to study the competition of two species of yeast: saccharomyces and schixosacharomyces.

The data was collected in 3 differents experimental settings, each of them repeated twice (experiment A and B):

Saccharomyces alone (single species setting)
Schixosacharomyces alone (single species setting)
Saccharomyces and Schixosacharomyces together (mixed species setting)

Model

The evolution of the population of yeasts is modelled with the competitive Lokta-Volterra equations.

Lotka-Volterra competition model

For a single species p:

$\frac{dp}{dt} = p (r - \alpha p)$

$p(t) = \frac{k}{1 + C e^{- r t}}$

r is the growth parameter
alpha is the (self) competition rate
k = r / alpha is the carrying capacity (steady state)
C is a constant determined by initial conditions

For two species:

$\begin{cases}\frac{dp_1}{dt} = p_1 (r_1 - \alpha_{1, 1} p_1 - \alpha_{1,2} p_2) \\\frac{dp_2}{dt} = p_2 (r_2 - \alpha_{2, 1} p_1 - \alpha_{2, 2} p_2)\end{cases}$

More generally, for N species (* is the element-wise multiplication):

$\frac{d\boldsymbol{p}}{dt} = \boldsymbol{p} * (\boldsymbol{r} - A \boldsymbol{p})$

Statistical model

The solutions of the ODEs can expressed as function of the initial conditions f₀, the parameters alpha and r and time t:

$p(t) = f(f_0, r, \alpha, t)$

Parameters are shared across experiments (fixed effects), except for the initial conditions which might vary from experiment to experiment.

The measurement process is modelled with a normal distribution:

In the case of an additive noise model:

$p_\mathit{obs}(t) \sim \mathcal{N} \big( p(t), \sigma^2 \big)$

In the case of an additive multiplicative noise model:

$\log \big( p_\mathit{obs}(t) \big) \sim \mathcal{N} \Big( \log \big( p(t) \big), \sigma^2 \Big)$

Priors

The initial conditions of the different experiments are unknown and treated as parameters, with the hierarchical prior:

$f_0 \sim \mathcal{N}^+(0, \sigma_{f_0}^2)$

Competition rates are regularised with the hierarchical prior:

$\alpha_{i, j} \sim \mathcal{C}^+(0, \sigma_\alpha)$

Weakly informative priors are chosen for the remaining parameters.

Results

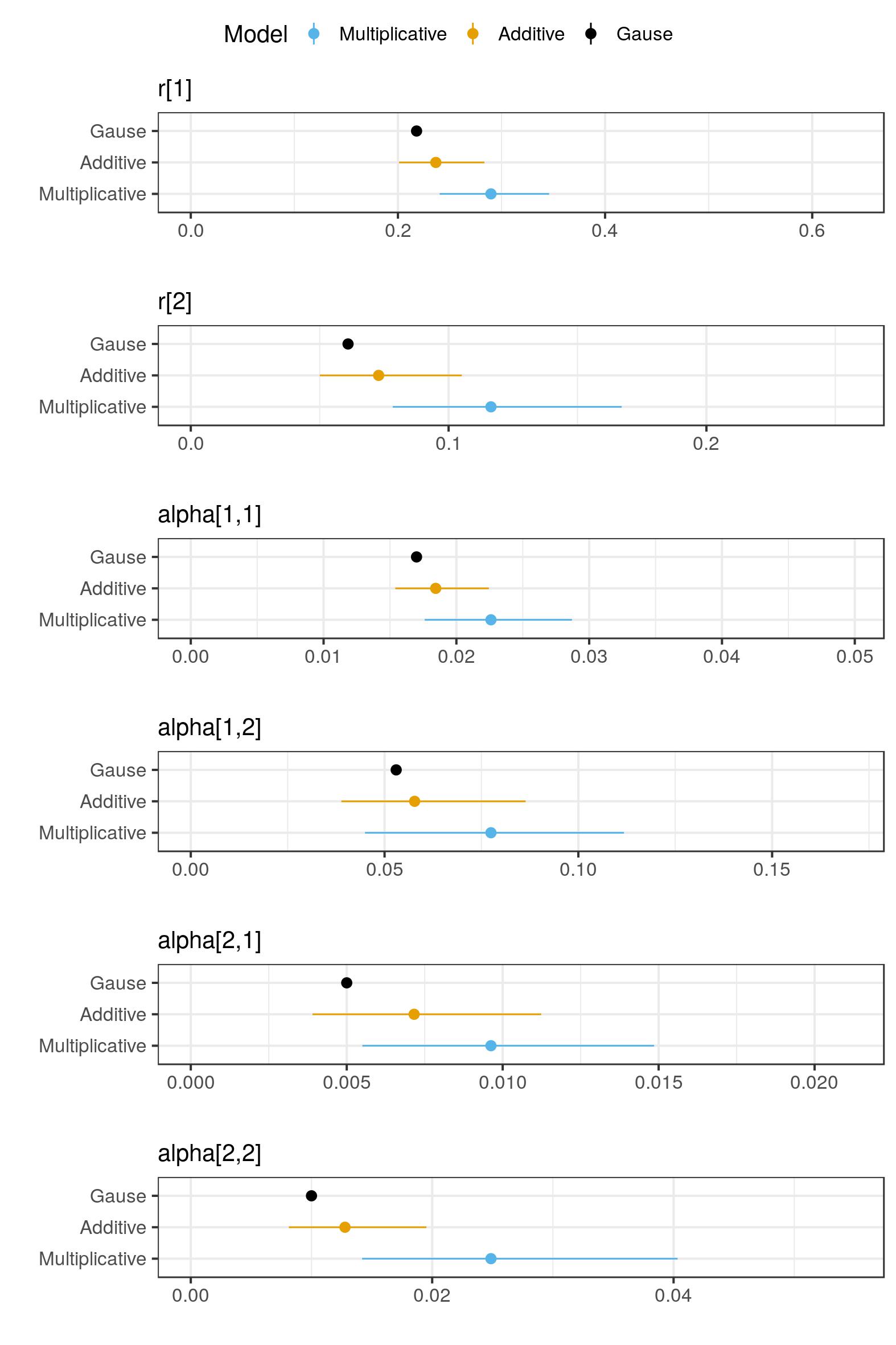
Posterior predictive checks are conducted and the likelihood is stored to perform model selection with the loo package. The additive and multiplicative models explain the data well but there is no strong evidence for choosing one model instead of the other (additive model is slightly favoured), although the experimental setup would suggest an additive noise.

Coefficients estimates for the two models (and those estimated in Gause's paper) are given below (error bars represents the 95% credible interval). The original estimates are similar to those of the additive error model but slightly differ to the multiplicate error model.

Future directions

Alternative regularisation of alpha matrix:
- Gaussian distribution (cf. ridge/L₂ regularisation)
- Laplace distribution (cf. lasso/L₁ regularisation)
- Horseshoe distribution
Sample k (steady states) instead of r (growth)
Introduce random effects at the experiment level
Compute Bayesian R-squared
Hard code alpha matrix as positive definite is the systems is stable a priori
Regularise r

ghurault/lvc_stan