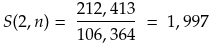Corso di Programmazione Concorrente e Parallela Su Cloud, Dipartimento di Informatica, Università degli Studi di Salerno
-Name: Gilberto Recupito , 0522500842
Il seguente progetto presenta le seguenti versioni:
- gol_animation.c : esecuzione della versione animata semplice di Game Of Life
- gol_correctness.c : esecuzione della versione che stampa ogni generazione per la verifica di correttezza di Game Of Life
- gol.c : esecuzione della versione che misura le prestazioni di scalabilità debole e forte di Game Of Life
- gol_misuring.c : esecuzione della versione che misura e salva su file le prestazioni di scalabilità debole e forte di Game Of Life(utilizzabile anche attraverso Makefile)
Per l'esecuzione del progetto è necessario eseguire le seguenti righe di comando:
- gol_animation.c:
mpicc gol_animation.c -o animation
mpirun -np <X> animation <N> <M> <G>
- gol_correctness.c:
mpicc gol_correctness.c -o correctness
mpirun -np <X> correctness <N> <M> <G>
- gol.c :
mpicc gol.c -o gol
mpirun -np <X> gol <N> <M> <G>
- gol_misuring.c :
mpicc gol_misuring.c -o gol_misuring
mpirun -np <X> gol <N> <M> <G> <FILE>
I parametri rappresentati sono i seguenti:
- X: Numero di processi
- N: Numero di righe della matrice
- M: Numero di colonne della matrice
- G: Numero di generazioni
- FILE: nome del file su cui scrivere i risultati
La soluzione proposta per la realizzazione di questo progetto prevede principalmente la risoluzione attraverso i seguenti step:
-
Creazione, Suddivisione e scattering della matrice:
-
Computazione di ogni singolo processo di ogni riga interna
-
Comunicazione delle righe esterne tra i processi e Computazione delle righe esterne
-
Gathering della matrice
La creazione della matrice è stata effettuata dal processo Master è utilizza la seguente struttura per la definizione di essa:
//Matrix world creator for Game of Life in MPI
typedef struct {
char * matrix;
int rows;
int columns;
}Pworld;
Problema affrontato : Allocazione della matrice In questo caso la matrice poteva essere definita come un array di puntatori dove ogni puntatore puntava a un array di caratteri. Questa proposta di soluzione riportava problemi successivi relativi alla comunicazione delle righe tra i processi, poichè l'allocazione delle righe non erano contigue tra loro e risalire alla posizione della riga successiva era risultato più complicato. Per risolvere questo problema si è pensato di allocare la memoria della matrice contiguamente definendo quindi un array di rows*columns elementi. Una volta creata la relazione tra quella che è la posizione della matrice e la posizione fisica nell'array è la seguente:
Sia A una matrice e B l'array corrispondente entrambi di n*m elementi
A[i][j] = B[(i*m)+j]
Una volta definita la struttura di tipo Pworld, il master creerà la matrice attraverso la seguente funzione:
Pworld* create_world(int n,int m);
L'inizializzazione della matrice avviene in maniera pseudocasuale attraverso la funzione init_world:
void init_world(Pworld * p,int seed)
Dove p rappresenta il mondo da inizializzare e seed il seme per la funzione di randomizzazione (rand())
Problema Affrontato: Suddivisione della matrice Questo problema principalmente presenta la suddivisione della matrice in sottomatrici da distribuire ai diversi processi. Tra le soluzioni proposte le più rilevanti e analizzate sono state:
- Per righe
- Per colonne
- Per sottomatrici
Per le tecniche 1 e 2 dobbiamo considerare la prima e l'ultima riga di ogni partizione distribuita come una riga esterna (ghost row), poichè serviranno ai processi adiacenti per effettuare completamente la computazione. Considerando quindi che ogni processo i quindi dovrà inviare una riga al processo i-1 e una riga al processo i+1 , avremmo per ogni generazione 2*p righe inviate.
Per la tecnica 3 invece dobbiamo considerare che per ogni cella nel bordo dobbiamo ricevere fino a 3 messaggi da 3 differenti processi, e in alcuni casi fino a 4 messaggi da 4 diversi processi.
Per questo motivo, al fine di ridurre l'overhead di comunicazione tra i processi, si è deciso di utilizzare una delle prime due tecniche.
In particolare, utilizzando C come linguaggio si è deciso di utilizzare la suddivisione per righe (1), poichè per la gestione dell'allocazione di memoria C presenta un orientamento di tipo row major.
Per la suddivisione della matrice è stata utilizzata il pattern di comunicazione Scatter, in particolare la funzione MPI_Scatterv(), dove nel nostro contesto, a differenza della classica funzione Scatter, ci permette di decidere quante righe inviare ad ogni processo.
MPI_Scatterv(p->matrix,sendcounts,displs,row,p->matrix,recv_count,row,0,MPI_COMM_WORLD)
In particolare vengono calcolate le posizioni iniziali (displs) da cui partire per ogni invio di riga, e la quantità di righe da inviare ad ogni processore, distribuendo omogeneamente una riga per ogni processore nel caso il numero di righe non è divisibile per il numero di processori. Per una migliore e più semplice suddivisione della matrice, è stato deciso di creare il datatype di comunicazione row, e di utilizzarlo per tutte le operazioni di comunicazione tra i processi:
MPI_Type_contiguous(m,MPI_CHAR,&row);
Dato che la matrice è stata allocata contiguamente, è stato deciso di definire un datatype contiguo.
Dopo che ogni processo riceve la sua partizione di matrice, è necessario analizzare la partizione secondo le seguenti definizioni:
-
Riga limite superiore: prima riga del processo i per il quale ogni elemento presente in questa riga ha bisogno dell'ultima riga del processo i-1.
-
Riga interna: riga del processo i per il quale ogni elemento presente in questa riga non ha bisogno di righe presenti in altri processi per la computazione della generazione.
-
Riga limite inferiore: prima riga del processo i per il quale ogni elemento presente in questa riga ha bisogno della prima riga del processo i+1.
Data questa differenziazione di righe, si è preferito che ogni processo computasse inizialmente le righe interne per poi passare alla computazione.
Facendo riferimento alla funzione compute() che comprende tutta la fase di computazione e comunicazione, calcoliamo inizialmente l'elemento della generazione successiva attraverso le seguenti funzioni:
int count_internalrow(Pworld * p, int n, int m);
int count_externalrow(Pworld * p, int n, int m);
- count_internalrow: conta il numero di celle vicine per la riga attuale rispetto alla cella (n,m)
- count_externalrow: conta il numero di celle vicine per la riga superiore o inferiore rispetto alla cella (n,m)
In riferimento a questi due metodi, il calcolo della condizione sul conteggio delle celle vive poi viene effettuato attraverso la funzione alive_conditioner()
char alive_conditioner(char cell,int count){
if(isAlive(cell)){
if(count<2||count>3){
return '0';
}else{
return '1';
}
}else{
if(count==3){
return '1';
}else{
return '0';
}
}
}
Quindi per ogni cella j di ogni sottomatrice compresa tra gli indici di riga 1 e rows-2 utilizzano il seguente snippet per il calcolo della generazione successiva:
for(int i=1;i<p->rows-1;i++){
for(int j=0;j<p->columns;j++){
//starting to count the nearest cells
int count=0;
//count alive cells in upper row
count+=count_externalrow(p,i-1,j);
//count alive cells in current row (need to not consider the current cell)
count+=count_internalrow(p,i,j);
//count alive cells in lower row
count+=count_externalrow(p,i+1,j);
//update cell
updated_world->matrix[(p->columns*i)+j] = alive_conditioner(p->matrix[(p->columns*i)+j],count);
}
}
Avendo effettuato una suddivisione della matrice per righe, ogni processo ha bisogno della riga inferiore e della riga superiore rispetto alla sottomatrice attuale. Definiamo quindi:
-
top_ghostrow: come la riga del processo i-1 necessaria come riga superiore alla sottomatrice attuale
-
bottom_ghostrow: come la riga del processo i+1 necessaria come riga inferiore alla sottomatrice attuale
Quindi ogni processo dovrà inviare corrispettivamente la prima e l'ultima riga della sua sottomatrice rispettivamente al processo i-1 e al processo i+1;
Il processo principalmente prevede i seguenti step:
- Invio non bloccante della riga superiore e inferiore
- Computazione delle righe interne
- Ricezione bloccante delle ghost rows e computazione delle righe esterne della matrice
Questa operazione è stata realizzata attraverso i metodi send_up() and send_down() Per questa operazione è stato deciso di utilizzare un invio non bloccante in modo che non bisogna aspettare il completamento per continuare la computazione.
/** Permit to send the communication row to the process above */
MPI_Request send_up(Pworld * p,int rank,MPI_Datatype* row,int p_size){
int rank_tosend;
if(Master(rank)){
rank_tosend=p_size-1;
}else{
rank_tosend=rank-1;
}
MPI_Request r;
MPI_Isend(&(p->matrix[0]),1,*row,rank_tosend,14,MPI_COMM_WORLD,&r);
return r;
}
/** Permit to send the communication row to the process below**/
MPI_Request send_down(Pworld * p,int rank,MPI_Datatype* row,int p_size){
MPI_Request r;
MPI_Isend(&(p->matrix[(p->columns)*(p->rows-1)]),1,*row,(rank+1)%p_size,14,MPI_COMM_WORLD,&r);
return r;
}
Essendo la struttura logica un toroide, è necessario definire come il processo precedente di 0 il processo n-1.
Analogamente, per la ricezione delle righe inviate dai processi adiacenti sono stati utilizzati i metodi receive_up() e receive_down():
/** Permit to receive the communication row from the process above**/
MPI_Request * receive_up(Pworld * p,int rank,MPI_Datatype* row,int p_size){
int rank_toreceive;
if(Master(rank)){
rank_toreceive=p_size-1;
}else{
rank_toreceive=rank-1;
}
MPI_Request * r;
MPI_Status s;
MPI_Recv(&p->matrix[0],1,*row,rank_toreceive,14,MPI_COMM_WORLD,&s);
return r;
}
/** Permit to receive the communication row from the process below**/
MPI_Request * receive_down(Pworld * p,int rank,MPI_Datatype* row,int p_size){
int rank_tosend;
if(Master(rank)){
rank_tosend=p_size-1;
}else{
rank_tosend=rank-1;
}
MPI_Request * r;
MPI_Status s;
MPI_Recv(&p->matrix[0],1,*row,(rank+1)%p_size,14,MPI_COMM_WORLD,&s);
return r;
}
Contrariamente all'invio, è necessario che le operazioni di receive siano completate per continuare la computazione. Per questo motivo si è deciso di utilizzare una receive bloccante.
Al termine della computazione le sottomatrici aggiornate saranno inviate tutte al processo Master. Per effettuare questa operazione si è deciso di utilizzare l'operazione Gatherv:
MPI_Gatherv(&(updated_p->matrix[0]),sendcounts[rank],row,pointer_matrix_to_start,sendcounts,displs,row,0,MPI_COMM_WORLD);
L'array sendcounts e displs utilizzati sono analoghi a quelli utilizzati per l'operazione di Scatterv.
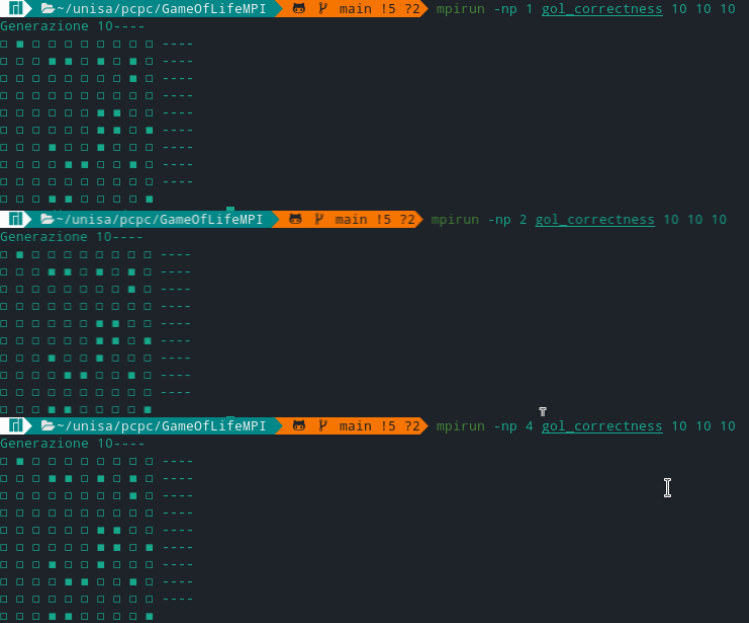
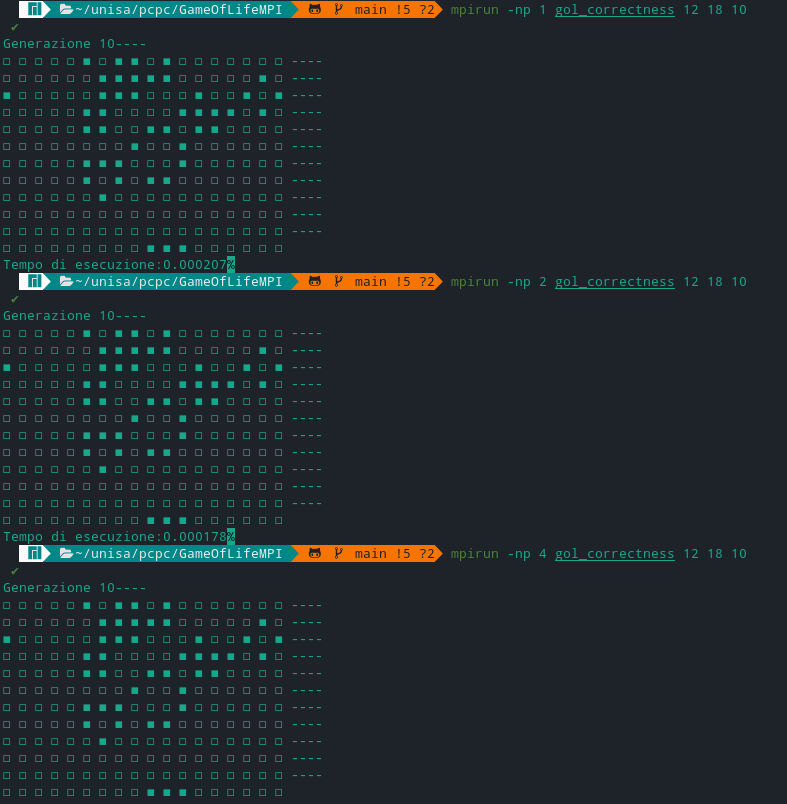
Per verificare la correttezza dell'algoritmo è stato utilizzata la versione gol_correctness.c, che ci permette di visualizzare il risultato di ogni generazione. Allo scopo di valutare la correttezza è stato deciso di verificare se al variare del numero di processori, l'algoritmo portasse lo stesso risultato considerando lo stessa matrice di input. In particolare per ottenere lo stesso input, la generazione della matrice viene effettuata attraverso una generazione casuale con lo stesso seme (in particolare il seme è 0):
//Initialize the world p with the seed 0
init_world(p,0);
L'esecuzione ha portato i seguenti risultati:
Per l'esecuzione e la misurazione è stato riportato l'utilizzo del makefile in modo da automatizzare le diverse esecuzioni sul cluster di macchine utilzzate. Nel contesto della misurazione sono state assegnate delle macchine di tipo t2.xlarge, quindi con 4 VCPU. Quindi sono state utilizzate 4 macchine per avere a disposizione fino a 16 VCPUs.
Per ogni test è stato deciso di eseguire ogni esecuzione che prevedesse l'utilizzo da 1 processo a 16 processi.
L'esecuzione e la misurazione di scalabilità di sistema è stata prefissata e progettata nel seguente modo:
Per effettuare i test è stato necessario utilizzare il file gol_misuring.c in modo da registrare i risultati in appositi file di tipo csv.
Per automatizzare i test è stato quindi deciso di utilizzare un Makefile (disponibile nel repository).
Per accedere alla misurazione del test basta quindi posizionarsi nella cartella del progetto GameOfLifeMPI e eseguire il seguente comando:
make
NB: modificare prima il Makefile per impostare le esecuzioni e le dimensioni dei test.
- Scalabilità Forte: Esecuzione dell'algoritmo con una dimensione prefissata della matrice.
| Dimensione test | Numero Processi | N | M | G |
|---|---|---|---|---|
| Little | da 1 a 16 | 200 | 200 | 100 |
| Medium | da 1 a 16 | 2000 | 2000 | 100 |
| Big | da 1 a 16 | 5000 | 5000 | 100 |
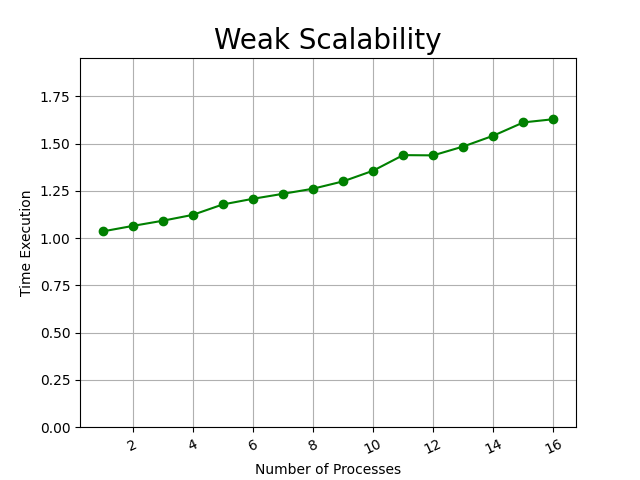
- Scalabilità Debole: Esecuzione dell'algoritmo con un rapporto processo/quantità di dati prefissato
| Dimensione test | Numero Processi | N | M | G |
|---|---|---|---|---|
| Little | da 1 a 16 | da 100 a 1600 | 100 | 100 |
| Medium | da 1 a 16 | da 1000 a 16000 | 1000 | 100 |
| Big | da 1 a 16 | da 2000 a 32000 | 1000 | 100 |
Per analizzare i risultati si tiene in considerazione l'utilizzo dell'algoritmo in sequenziale e dell'utilizzo in parallelo per vedere il suo effetto.
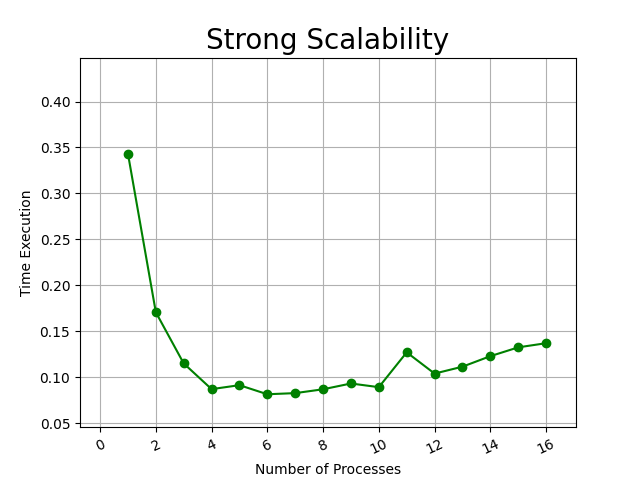
- Little : Matrice 100x100 (Tempo in secondi)
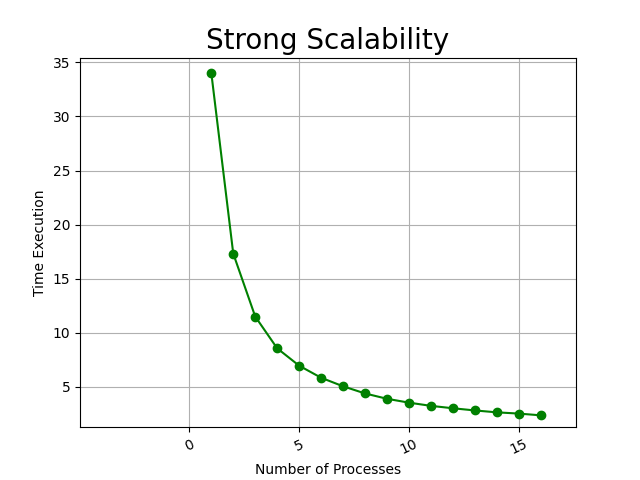
Già da un'esecuzione di bassa computazione dovuta alle piccole dimensioni della matrice è possibile vedere l'effetto importante che dà l'algoritmo parallelo rispetto al sequenziale in tempi di esecuzioni. Importante notare come da un numero di processi maggiore di 9 si è ritrovato un aumento del tempo di esecuzione, possibilmente dovuto al tempo di comunicazione tra i diversi processi. In questo test il risultato migliore è stato registrato con 6 processi con il tempo di: 0.081532 secondi.
- Medium : Matrice 2000x2000 (Tempo in secondi)
Proporzionalmente a quanto detto prima, al crescere della matrice l'effetto della parallelizzazione aumenta con un notevole impatto. Al crescere del numero di processi, lo speedup relativo non aumenta considerevolmente, ma comunque non porta a considerevoli peggioramenti.
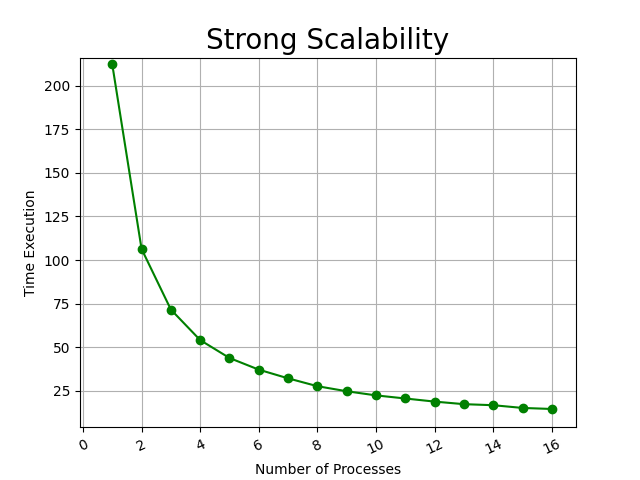
- Big : Matrice 5000x5000 (Tempo in secondi)
In definitiva eseguendo il test su una matrice più grande, manteniamo gli stessi effetti di parallelizzazione. Registriamo quindi uno speedup relativo pari a:
- Little : Matrice 100x100 (Tempo in secondi)
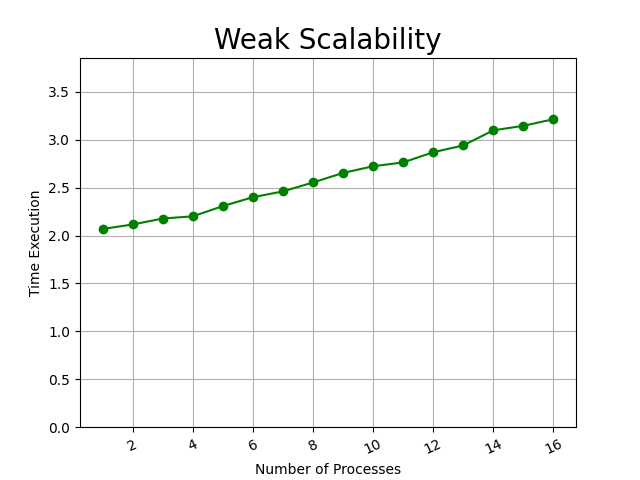
- Medium : Matrice 2000x2000 (Tempo in secondi)
- Big : Matrice 5000x5000 (Tempo in secondi)
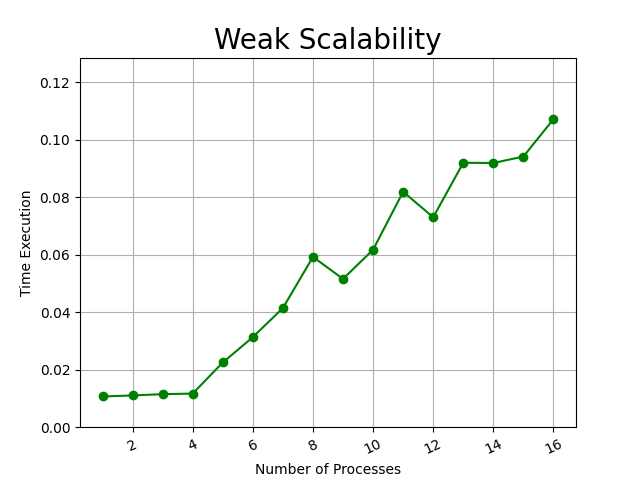
Per quanto riguarda i risultati di scalabilità debole del nostro sistema, possiamo vedere come mantenendo costante il numero di dati da computare per ogni processo, il tempo di esecuzione aumenta. Notando particolari effetti nell'esecuzione piccola, è possibile che l'aumento del tempo di esecuzione sia dovuto alla comunicazione tra i processi per lo scambio delle righe. Infine è possibile notare che questo è effetto è visibile solo per una bassa quantità di dati da computare, e quindi non crea effetti considerevoli e che aumentano proporzionalmente alla dimensione dei dati di computazione, ma in quantità di dati maggiori l'algoritmo riesce a non avere variazioni considerevoli di esecuzione di tempo all'aumento dei dati e quindi si può considerare che i dati possono essere equalmente distribuiti tra i diversi processi.
In definitiva questo progetto mostra un notevole effetto e importanza nell'utilizzo della parallelizzazione per determinati algoritmi, portando risultati determinanti. Per ottenere risultati eccellenti però, è necessario far fronte a differenti problemi che molte volte sono anche impossibili da mitigare, come l'overhead di comunicazione e il sovraccarico delle macchine.