Make sure you are using robo-nd VM or have Ubuntu+ROS installed locally.
Check the version of gazebo installed on your system using a terminal:
$ gazebo --versionTo run projects from this repository you need version 7.7.0+ If your gazebo version is not 7.7.0+, perform the update as follows:
$ sudo sh -c 'echo "deb http://packages.osrfoundation.org/gazebo/ubuntu-stable `lsb_release -cs` main" > /etc/apt/sources.list.d/gazebo-stable.list'
$ wget http://packages.osrfoundation.org/gazebo.key -O - | sudo apt-key add -
$ sudo apt-get update
$ sudo apt-get install gazebo7Once again check if the correct version was installed:
$ gazebo --versionFor the rest of this setup, catkin_ws is the name of active ROS Workspace, if your workspace name is different, change the commands accordingly
If you do not have an active ROS workspace, you can create one by:
$ mkdir -p ~/catkin_ws/src
$ cd ~/catkin_ws/
$ catkin_makeNow that you have a workspace, clone or download this repo into the src directory of your workspace:
$ cd ~/catkin_ws/src
$ git clone https://github.com/udacity/RoboND-Kinematics-Project.gitNow from a terminal window:
$ cd ~/catkin_ws
$ rosdep install --from-paths src --ignore-src --rosdistro=kinetic -y
$ cd ~/catkin_ws/src/RoboND-Kinematics-Project/kuka_arm/scripts
$ sudo chmod +x target_spawn.py
$ sudo chmod +x IK_server.py
$ sudo chmod +x safe_spawner.shBuild the project:
$ cd ~/catkin_ws
$ catkin_makeAdd following to your .bashrc file
export GAZEBO_MODEL_PATH=~/catkin_ws/src/RoboND-Kinematics-Project/kuka_arm/models
source ~/catkin_ws/devel/setup.bash
For demo mode make sure the demo flag is set to "true" in inverse_kinematics.launch file under /RoboND-Kinematics-Project/kuka_arm/launch
In addition, you can also control the spawn location of the target object in the shelf. To do this, modify the spawn_location argument in target_description.launch file under /RoboND-Kinematics-Project/kuka_arm/launch. 0-9 are valid values for spawn_location with 0 being random mode.
You can launch the project by
$ cd ~/catkin_ws/src/RoboND-Kinematics-Project/kuka_arm/scripts
$ ./safe_spawner.shIf you are running in demo mode, this is all you need. To run your own Inverse Kinematics code change the demo flag described above to "false" and run your code (once the project has successfully loaded) by:
$ cd ~/catkin_ws/src/RoboND-Kinematics-Project/kuka_arm/scripts
$ rosrun kuka_arm IK_server.pyOnce Gazebo and rviz are up and running, make sure you see following in the gazebo world:
- Robot
- Shelf
- Blue cylindrical target in one of the shelves
- Dropbox right next to the robot
If any of these items are missing, report as an issue.
Once all these items are confirmed, open rviz window, hit Next button.
To view the complete demo keep hitting Next after previous action is completed successfully.
Since debugging is enabled, you should be able to see diagnostic output on various terminals that have popped up.
The demo ends when the robot arm reaches at the top of the drop location.
There is no loopback implemented yet, so you need to close all the terminal windows in order to restart.
In case the demo fails, close all three terminal windows and rerun the script.
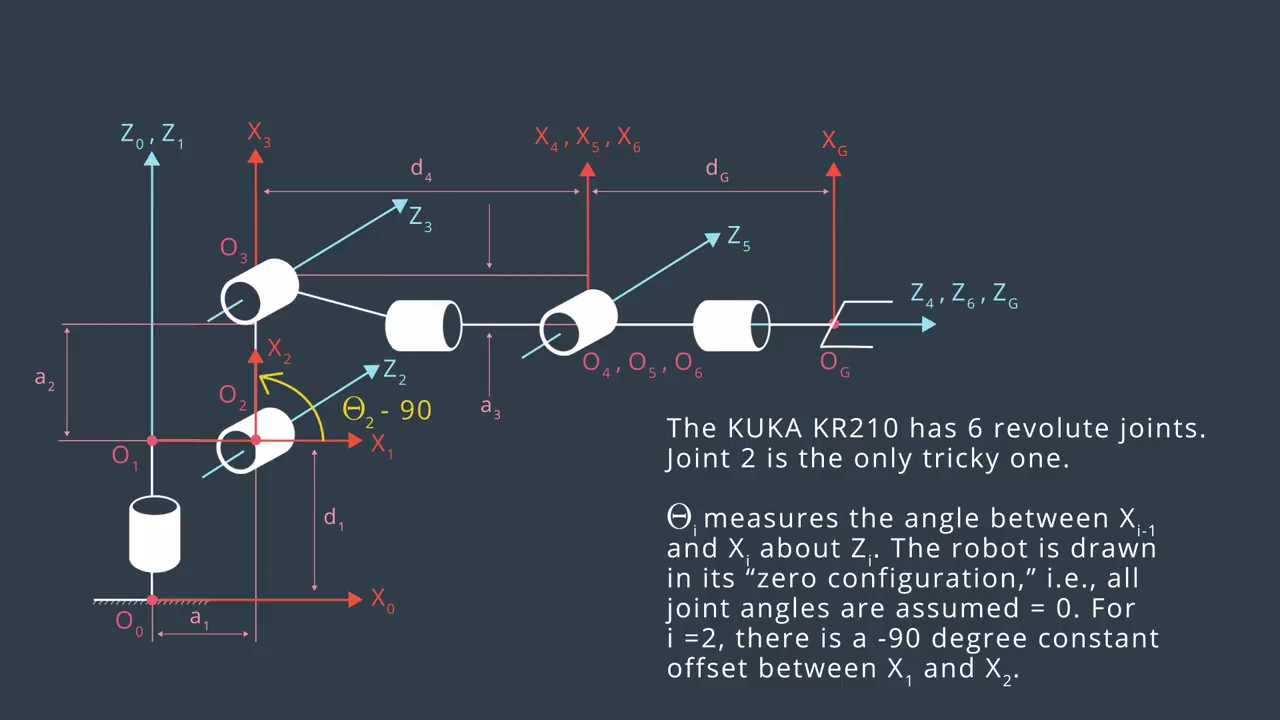
1. The kinematics analysis was performed using the annotated figure of the robot below. The figure shows the frames attached to each joint and labels from the DH parameter table.
| Links | alpha(i-1) | a(i-1) | d(i-1) | theta(i) |
|---|---|---|---|---|
| 0->1 | 0 | 0 | 0.75 | q1 |
| 1->2 | - pi/2 | 0.35 | 0 | -pi/2 + q2 |
| 2->3 | 0 | 1.25 | 0 | q3 |
| 3->4 | - pi/2 | -0.054 | 1.5 | q4 |
| 4->5 | pi/2 | 0 | 0 | q5 |
| 5->6 | - pi/2 | 0 | 0 | q6 |
| 6->EE | 0 | 0 | 0.303 | 0 |
Using the DH table above the indivitual transformation matrices were defined between each two subsequent links (i=1..7) using this general structure:
T(i-1)_i = Matrix([[ cos(qi), -sin(qi), 0, a(i-1)],
[sin(qi)*cos(alpha(i-1), cos(qi)*cos(alpha(i-1)), -sin(alpha(i-1)), -sin(alpha(i-1))*di],
[sin(qi)*sin(alpha(i-1), cos(qi)*sin(alpha(i-1)), cos(alpha(i-1)), cos(alpha(i-1))*di],
[ 0, 0, 0, 1]])
Which results in those individual HT matrices:
T0_1 = Matrix([[ cos(q1), -sin(q1), 0, a0],
[sin(q1)*cos(alpha0), cos(q1)*cos(alpha0), -sin(alpha0), -sin(alpha0)*d1],
[sin(q1)*sin(alpha0), cos(q1)*sin(alpha0), cos(alpha0), cos(alpha0)*d1],
[ 0, 0, 0, 1]])
T1_2 = Matrix([[ cos(q2), -sin(q2), 0, a1],
[sin(q2)*cos(alpha1), cos(q2)*cos(alpha1), -sin(alpha1), -sin(alpha1)*d2],
[sin(q2)*sin(alpha1), cos(q2)*sin(alpha1), cos(alpha1), cos(alpha1)*d2],
[ 0, 0, 0, 1]])
T2_3 = Matrix([[ cos(q3), -sin(q3), 0, a2],
[sin(q3)*cos(alpha2), cos(q3)*cos(alpha2), -sin(alpha2), -sin(alpha2)*d3],
[sin(q3)*sin(alpha2), cos(q3)*sin(alpha2), cos(alpha2), cos(alpha2)*d3],
[ 0, 0, 0, 1]])
T3_4 = Matrix([[ cos(q4), -sin(q4), 0, a3],
[sin(q4)*cos(alpha3), cos(q4)*cos(alpha3), -sin(alpha3), -sin(alpha3)*d4],
[sin(q4)*sin(alpha3), cos(q4)*sin(alpha3), cos(alpha3), cos(alpha3)*d4],
[ 0, 0, 0, 1]])
T4_5 = Matrix([[ cos(q5), -sin(q5), 0, a4],
[sin(q5)*cos(alpha4), cos(q5)*cos(alpha4), -sin(alpha4), -sin(alpha4)*d5],
[sin(q5)*sin(alpha4), cos(q5)*sin(alpha4), cos(alpha4), cos(alpha4)*d5],
[ 0, 0, 0, 1]])
T5_6 = Matrix([[ cos(q6), -sin(q6), 0, a5],
[sin(q6)*cos(alpha5), cos(q6)*cos(alpha5), -sin(alpha5), -sin(alpha5)*d6],
[sin(q6)*sin(alpha5), cos(q6)*sin(alpha5), cos(alpha5), cos(alpha5)*d6],
[ 0, 0, 0, 1]])
T6_G = Matrix([[ cos(q7), -sin(q7), 0, a6],
[sin(q7)*cos(alpha6), cos(q7)*cos(alpha6), -sin(alpha6), -sin(alpha6)*d7],
[sin(q7)*sin(alpha6), cos(q7)*sin(alpha6), cos(alpha6), cos(alpha6)*d7],
[ 0, 0, 0, 1]])
After the individual HTs were calculated the base_link-->gripper combined HT was calculated by multiplying the subsequent HT matrices:
T0_G = T0_1*T1_2*T2_3*T3_4*T4_5*T5_6*T6_G
3. Decoupling of Inverse Kinematics problem into Inverse Position Kinematics and inverse Orientation Kinematics
KR210 robot has spherical wrist (the last 3 revolute joints axes intersect in a single point) therefore the IK problem can be decoupled to Position problem and Orientation problem. For the inverse position problem the first step is to calculate the wrist center (joint4) by subtracting the rotated length of link 6 from the gripper required position:
nx = Rot_G[0,2]
ny = Rot_G[1,2]
nz = Rot_G[2,2]
d = 0.303
# WC - Wrist Center
wx = px - d*nx
wy = py - d*ny
wz = pz - d*nz
Given the required position of the wrist center, the first three angles can be calculated using trigonometry starting with theta1 by projecting the wrist center to x-y plane as follows:
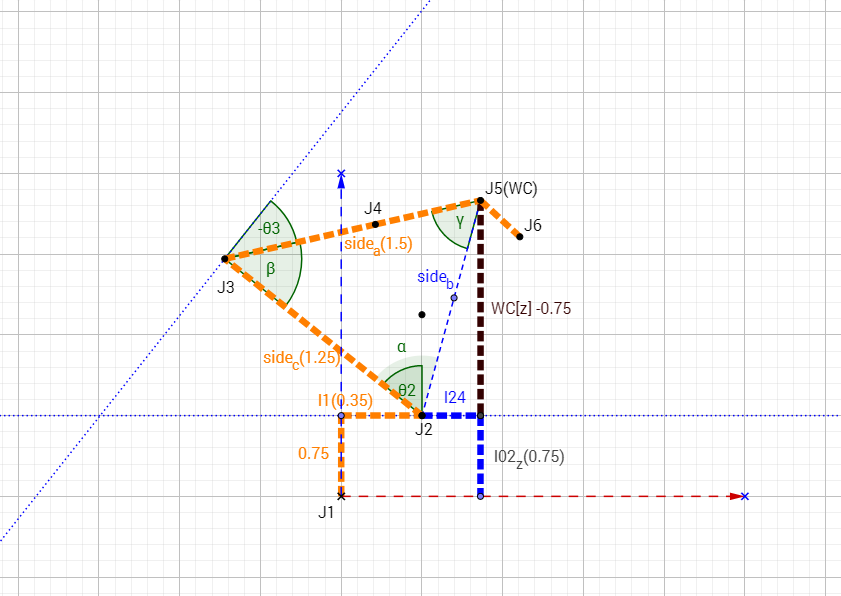
For theta2 and theta3 we use a triangle formed by J2, J3 and J5(WC). Following image visualizes the angle and link definitions:
The last three are theta4, theta4 and theta6 and those angles affect only the orientation of the gripper. Here the HTs we calculated previously are coming handy. We first find the rotation matrix from frame3 to frame6:
R0_3 = T0_1[0:3,0:3]*T1_2[0:3,0:3]*T2_3[0:3,0:3]
R3_6 = R0_3.inv("LU") * Rot_G
Where:
R0_3 - Rotation matrix from frame0 to frame3
T0_1 - Homogenous Transform matrix from frame0 to frame1
Rot_G - Rotation matrix from frame0 to gripper (frame6)
R3_6 - Rotation matrix from frame3 to frame6
Now we can extract the last three theta values using Euler angles using the method described here: http://www.staff.city.ac.uk/~sbbh653/publications/euler.pdf
x = R3_6[0,2]
y = R3_6[1,2]
z = R3_6[2,2]
theta4 = atan2(z, -x)
theta5 = atan2(sqrt(x**2 + z**2), y)
theta6 = atan2(-R3_6[1,1], R3_6[1,0])
During the implementation I encountered several issues as described below:
- Debugging - to validate the HT matrices correctness I evaluated the matrices with all theta (qi) angles equal to 0 and compared to the "Absolute Position" field in Rviz when the angles are also set to 0.
- Multiple solutions - since the solution for the theta4-6 angles is not unique it can not be compared with known answer therefore I evaluated the HT matrix from base to gripper at the calculated theta values and compared with the required pose of the gripper.
- Optimization - some of the inverse kinematics operations take considerable amount of compute resources therefore most of the matrices that do not change during execution, such as the T0_1, T1_2 etc..., are precomputed outside of
handle_calculate_IKfunction so they run only once when the server is started, saving around 0.8sec per trajectory.