Ashlar: Mesh Properties for Stone Datasets

This repository is provided as a supplement to the paper Multimodal Robotic Construction with On-Site Materials.
For closed triangular meshes (i.e. representing stones), we provide methods for computing meta-faces using iterative variational shape approximation, form and mass properties, and the ashlarness metric.

ashlar noun

ash·lar | \ ˈash-lər \
1: hewn or squared stone
also : masonry of such stone

Dependencies

This project uses the geometry processing library libigl, and the only dependencies are STL, Eigen, libigl and the dependencies of the igl::opengl::glfw::Viewer (OpenGL, glad and GLFW). The CMake build system will automatically download libigl and its dependencies using CMake FetchContent, thus requiring no setup on your part.

Compile

Compile this project using the standard cmake routine:

mkdir build && cd build
cmake ..
make

This should find and build the dependencies and create the ashlar binary.

Run

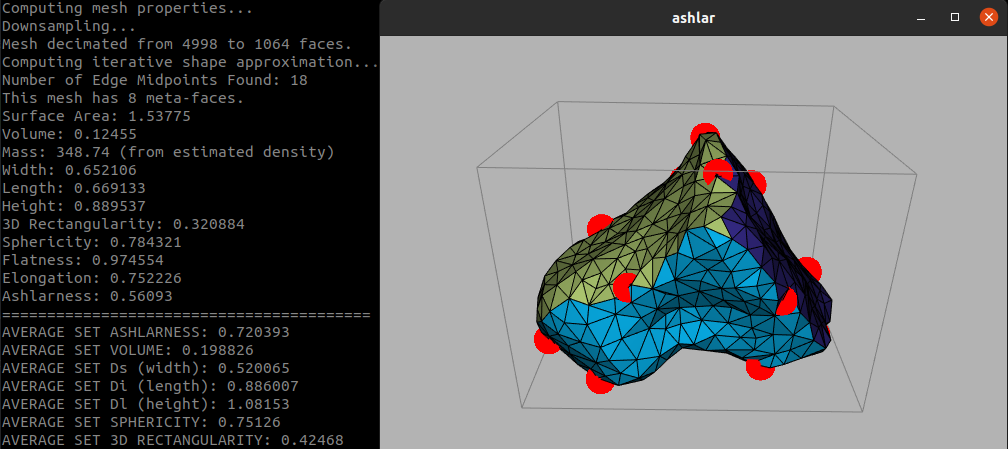
For computing the properties of a single stone, execute with the additional argument of the 3D triangle mesh file location. For example, to use the provided sample mesh 923.obj, execute:

./ashlar  ../mesh/923.obj

For processing many mesh files at once (i.e. to assess the volume, dimensions, and form properties of a dataset of stone models), simply launch with a wildcard variable for all files in a specified directory:

./ashlar  ../mesh/*.obj

In both cases, the computed properties should print to the console, and a viewer will launch displaying the latest stone, with colored meta-faces, edge midpoints, and bounding box (the mesh is reoriented using PCA).

Output

At each run, the software should output a log file logger.csv in the main project directory which includes salient properties of each stone. This can be useful, for example, for plotting or assessing the distribution of properties in a dataset of stones using external tools. Note that this log file is overwritten at each run.

File formats

Input files should be in one of the following formats: obj, off, stl, wrl, ply, mesh

Models should be clean, closed triangle meshes of stone-like objects: disjoint pieces, many duplicate vertices, etc. will likely cause issues.
We assume the units are in meters (i.e. for mass properties), but in practice the majority of the other attributes are scale invariant.
To speed up the meta-face estimation and for improved consistency with our existing dataset, we downsample the input mesh based on its volume and surface area prior to VSA computation (but after computing other geometric properties). This decimation is by default configured such that the mesh has approximately 500 faces per square meter if the stone were scaled to a volume of 1/3 m3.

Meta-face Estimation

The face estimation relies on the iterative seed-and-flood approach of Variational Shape Approximation, which attempts to find a distortion-minimizing set of $k$ meta-faces for a given triangle mesh. In our case, we iteratively increment $k$ after performing a maximum number of sub-iterations (default 10) per $k$ until a maximal $\mathcal{L}^{2,1}$ error metric has been achieved for all regions (default 0.26). The process automatically returns at a maximal region count $k$ (default 25).

Ashlarness

The ashlarness value attempts to provide a more suitable metric for the "stackability" of a set of stones. Given the estimated meta-faces of a stone with area $\mathit{A_s}$, and after aligning the stone to its approximate minimal bounding box (using PCA), we first identify a single broad meta-face whose area-weighted proxy normal is most aligned with either of the two largest faces of the stone bounding box. Using the area and unit normal of this meta-face as $\mathit{A_i}$ and $\mathbf{n_i}$, we iterate over the remaining meta-faces with respective areas and normals $\mathit{A_x}$ and $\mathbf{n_x}$ to find the single opposing face that produces the highest ashlarness value

$\arg \max_{x}\frac{1}{3}\big(\frac{\min{\mathit{A_i},\mathit{A_x}}}{\max{\mathit{A_i},\mathit{A_x}}}{+}\frac{\mathit{A_i}+\mathit{A_x}}{\mathit{A_s}}{+}(\mathbf{n_i} \cdot \mathbf{n_x})^2 \big)$

As such, stones with two parallel faces that are equivalent in area, and whose combined area makes up a large percentage of the total stone area have higher ashlarness (range 0-1). A visual distribution of the typical value range for this metric can be found in the below image from our paper:

Local libigl

To use a local copy of libigl rather than downloading the repository via FetchContent, you can use the CMake cache variable FETCHCONTENT_SOURCE_DIR_LIBIGL when configuring your CMake project for the first time:

cmake -DFETCHCONTENT_SOURCE_DIR_LIBIGL=<path-to-libigl> ..

When changing this value, do not forget to clear your CMakeCache.txt, or to update the cache variable via cmake-gui or ccmake.

References

If using this repository for academic work, we thank you for citing A framework for robotic excavation and dry stone construction using on-site materials

@article{johns_framework_2023,
	title = {A framework for robotic excavation and dry stone construction using on-site materials},
	volume = {8},
	doi = {10.1126/scirobotics.abp9758},
	number = {84},
	journal = {Science Robotics},
	author = {Johns, Ryan Luke and Wermelinger, Martin and Mascaro, Ruben and Jud, Dominic and Hurkxkens, Ilmar and Vasey, Lauren and Chli, Margarita and Gramazio, Fabio and Kohler, Matthias and Hutter, Marco},
	month = nov,
	year = {2023},
}

The Variational Shape Approximation approach for finding meta-faces is presented in

@article{10.1145/1015706.1015817,
author = {Cohen-Steiner, David and Alliez, Pierre and Desbrun, Mathieu},
title = {Variational Shape Approximation},
year = {2004},
issue_date = {August 2004},
publisher = {Association for Computing Machinery},
address = {New York, NY, USA},
volume = {23},
number = {3},
issn = {0730-0301},
url = {https://doi.org/10.1145/1015706.1015817},
doi = {10.1145/1015706.1015817},
journal = {ACM Trans. Graph.},
month = {aug},
pages = {905–914},
numpages = {10}
}

Mass properties are computed using the method described in

@article{10.1145/2601097.2601157,
author = {B\"{a}cher, Moritz and Whiting, Emily and Bickel, Bernd and Sorkine-Hornung, Olga},
title = {Spin-It: Optimizing Moment of Inertia for Spinnable Objects},
year = {2014},
issue_date = {July 2014},
publisher = {Association for Computing Machinery},
address = {New York, NY, USA},
volume = {33},
number = {4},
issn = {0730-0301},
url = {https://doi.org/10.1145/2601097.2601157},
doi = {10.1145/2601097.2601157},
journal = {ACM Trans. Graph.},
month = {jul},
articleno = {96},
numpages = {10}
}

For the visualization of meta-faces, with non-overlappling colors, we use the four color implementation of okaydemir, modified for a simplified eigen interface.

gramaziokohler/ashlar