[LeetCode] 240. Search a 2D Matrix II
grandyang opened this issue · 1 comments
Write an efficient algorithm that searches for a target value in an m x n integer matrix. The matrix has the following properties:
- Integers in each row are sorted in ascending from left to right.
- Integers in each column are sorted in ascending from top to bottom.
Example 1:
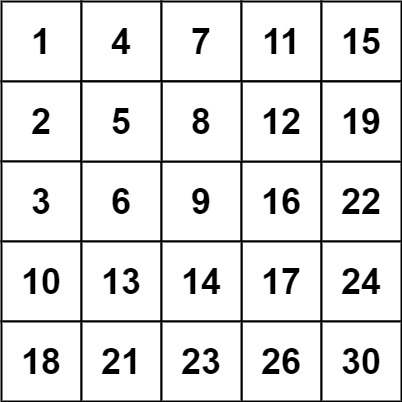
Input: matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
Output: true
Example 2:
Input: matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
Output: false
Constraints:
m == matrix.lengthn == matrix[i].length1 <= n, m <= 300-109 <= matix[i][j] <= 109- All the integers in each row are sorted in ascending order.
- All the integers in each column are sorted in ascending order.
-109 <= target <= 109
突然发现 LeetCode 很喜欢从 LintCode 上盗题,这是逼我去刷 LintCode 的节奏么?! 这道题让我们在一个二维数组中快速的搜索的一个数字,这个二维数组各行各列都是按递增顺序排列的,是之前那道 Search a 2D Matrix 的延伸,那道题的不同在于每行的第一个数字比上一行的最后一个数字大,是一个整体蛇形递增的数组。所以那道题可以将二维数组展开成一个一位数组用一次二查搜索。而这道题没法那么做,这道题有它自己的特点。如果我们观察题目中给的那个例子,可以发现有两个位置的数字很有特点,左下角和右上角的数。左下角的 18,往上所有的数变小,往右所有数增加,那么就可以和目标数相比较,如果目标数大,就往右搜,如果目标数小,就往上搜。这样就可以判断目标数是否存在。当然也可以把起始数放在右上角,往左和下搜,停止条件设置正确就行。代码如下:
class Solution {
public:
bool searchMatrix(vector<vector<int> > &matrix, int target) {
if (matrix.empty() || matrix[0].empty()) return false;
if (target < matrix[0][0] || target > matrix.back().back()) return false;
int x = matrix.size() - 1, y = 0;
while (true) {
if (matrix[x][y] > target) --x;
else if (matrix[x][y] < target) ++y;
else return true;
if (x < 0 || y >= matrix[0].size()) break;
}
return false;
}
};
Github 同步地址:
类似题目:
参考资料:
https://leetcode.com/problems/search-a-2d-matrix-ii/
https://leetcode.com/problems/search-a-2d-matrix-ii/discuss/66139/C%2B%2B-search-from-top-right
https://leetcode.com/problems/search-a-2d-matrix-ii/discuss/66140/My-concise-O(m%2Bn)-Java-solution
看到一种算法可以将效率提高到log(m)+log(n)的, 核心是二分法
class Solution {
public:
bool searchMatrix(vector<vector<int>>& matrix, int target) {
if(matrix.empty() || matrix[0].empty()) return false;
return searchRect(matrix,target,0,0,matrix.size()-1,matrix[0].size()-1);
}
bool searchRect(vector<vector<int>>& matrix, int target,
int top, int left, int bottom, int right) {
//search if the target is inside the rectangular matrix[top:bottom][left:right]
//each time we discard 1/4 of all elements
//time complexity O( log(mn)/log(4/3) ) = O(logm + logn)
if(top>bottom || left>right)
return false;
int x = (top+bottom)/2;
int y = (left+right)/2;
int center = matrix[x][y];
if(center > target){
return
searchRect(matrix,target,top,left,x-1,right) ||
searchRect(matrix,target,x,left,bottom,y-1);
}
else if(center < target){
return
searchRect(matrix,target,x+1,left,bottom,right) ||
searchRect(matrix,target,top,y+1,x,right);
}
else
return true;
}
};