Elle
Elle is a transactional consistency checker for black-box databases. Based purely on client observations of transactions, and given some minimal constraints on datatypes and operations, it can tell you whether that observation exhibits a variety of transactional anomalies. Like a clever lawyer, Elle looks for a sequence of events in a story which couldn't possibly have happened in that order, and uses that inference to prove the story can't be consistent.
In a nutshell, Elle is:
- General: Elle works over a variety of datatypes and places only minimal, practical constraints on transaction structure.
- Efficient: Elle is ~linear in history length, and ~constant, rather than exponential, with respect to concurrency.
- Effective: Elle has found unexpected anomalies in every database we've checked, ranging from internal consistency violations to anti-dependency cycles to dirty read to lost updates to realtime violations.
- Sound: Elle can find every (non-predicate) anomaly from Adya, Liskov, & O'Neil's Generalized Isolation Level Definitions.
- Elucidative: Elle can point to a minimal set of transactions which witness a consistency violation; its conclusions are easy to understand and verify.
This repository encompasses a Clojure implementation of the Elle consistency checker and its accompanying test suite, which you can use to check your own histories. Our paper provides deep insight into the goals and intuition behind Elle, and a rough formalization of its soundness proof. A nowhere-near-complete formal proof sketch is written in the Isabelle/HOL proof language.
If you want to check a database using Elle, see https://jepsen.io; Elle comes built-in. If you want to use Elle to check your own histories without using Jepsen, you can add Elle as a dependency to any JVM project, and invoke its checker functions directly. If you're working in a non-JVM language, you can write your history to a file or stream, and call a small wrapper program to produce output.
Elle is still under active development, and we're not 100% confident in its inference rules yet. Jepsen recommends checking reported anomalies by hand to make sure they're valid. If you'd like to contribute, we'd especially welcome your help in the formal proof, and in rigorously defining consistency models.
Questions? Read the paper!
Demo
First, you'll need a copy of Graphviz installed.
Imagine a database where each object (identified by keys like :x or :y) is
a list of numbers. Transactions are made up of reads [:r :x [1 2 3]], which
return the current value of the given list, and writes [:append :y 4], which
append a number to the end of the list.
=> (require '[elle.list-append :as a])
nilWe construct a history of three transactions, each of which is known to
have committed (:type :ok). The first transaction appends 1 to :x and
observes :y = [1]. The second appends 2 to :x and 1 to :y. The third
observes x, and sees its value as [1 2].
=> (def h [{:type :ok, :value [[:append :x 1] [:r :y [1]]]}
{:type :ok, :value [[:append :x 2] [:append :y 1]]}
{:type :ok, :value [[:r :x [1 2]]]}])
hNow, we ask Elle to check this history, expecting it to be serializable, and
have it dump anomalies to a directory called out/.
=> (pprint (a/check {:consistency-models [:serializable], :directory "out"} h))
{:valid? false,
:anomaly-types (:G1c),
:anomalies
{:G1c
[{:cycle
[{:type :ok, :value [[:append :x 2] [:append :y 1]]}
{:type :ok, :value [[:append :x 1] [:r :y [1]]]}
{:type :ok, :value [[:append :x 2] [:append :y 1]]}],
:steps
({:type :wr, :key :y, :value 1, :a-mop-index 1, :b-mop-index 1}
{:type :ww,
:key :x,
:value 1,
:value' 2,
:a-mop-index 0,
:b-mop-index 0}),
:type :G1c}]},
:not #{:read-committed},
:also-not
#{:consistent-view :cursor-stability :forward-consistent-view
:monotonic-atomic-view :monotonic-snapshot-read :monotonic-view
:repeatable-read :serializable :snapshot-isolation
:strict-serializable :update-serializable}}Here, Elle can infer the write-read relationship between T1 and T2 on the basis
of their respective reads and writes. The write-write relationship between T2
and T1 is inferrable because T3 observed x = [1,2], which constrains the
possible orders of appends. This is a G1c anomaly: cyclic information flow. The
:cycle field shows the operations in that cycle, and :steps shows the
dependencies between each pair of operations in the cycle.
On the basis of this anomaly, Elle has concluded that this history is not read-committed---this is the weakest level Elle can demonstrate is violated. In addition, several stronger isolation levels, such as consistent-view and update-serializable, are also violated by this history.
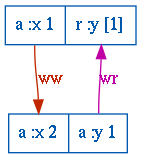
Let's see the G1c anomaly in text:
$ cat out/G1c.txt
G1c #0
Let:
T1 = {:type :ok, :value [[:append :x 2] [:append :y 1]]}
T2 = {:type :ok, :value [[:append :x 1] [:r :y [1]]]}
Then:
- T1 < T2, because T2 observed T1's append of 1 to key :y.
- However, T2 < T1, because T1 appended 2 after T2 appended 1 to :x: a contradiction!
In the out/G1c directory, you'll find a corresponding plot.
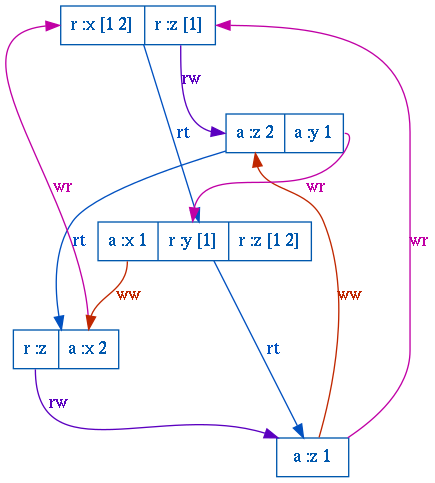
In addition to rendering a graph for each individual cycle, Elle generates a plot for each strongly-connected component of the dependency graph. This can be helpful for getting a handle on the scope of an anomalous behavior, whereas cycles show as small a set of transactions as possible. Here's a plot from a more complex history, involving realtime edges, write-write, write-read, and read-write dependencies:
Usage
As a user, your main entry points into Elle will be elle.list-append/check
and elle.rw-register/check. Both namespaces also have code for generating
sequences of transactions which you can apply to your database; see, for
example, elle.list-append/gen.
Elle has a broad variety of anomalies and consistency models; see
elle.consistency-model for their definitions. Not every anomaly is
detectable, but we aim for completeness.
If you'd like to define your own relationships between transactions, see
elle.core.
Observed Histories
Elle expects its observed histories in the same format as Jepsen. An observed history should be a list of operations in real-time order, where each operation is a map of the form:
{:type One of :invoke, ok, :info, :fail
:process A logical identifier for a single thread of execution
:value A transaction; structure and semantics vary}Each process should perform alternating :invoke and :ok/:info/:fail
operations. :ok indicates the operation definitely committed. :fail
indicates it definitely did not occur--e.g. it was aborted, was never submitted
to the database, etc. :info indicates an indeterminate state; the transaction
may or may not have taken place. After an :info, a process may not perform another operation; the invocation remains open for the rest of the history.
Types of Tests
elle.core: The heart of Elle's inference system. Computes transaction graphs and finds cycles over them. Includes general-purpose graphs for per-process and realtime orders.elle.rw-register: Write/Read registers. Weaker inference rules, but applicable to basically all systems. Objects are registers; writes blindly replace values.elle.list-append: Elle's most powerful inference rules. Objects are lists, writes append unique elements to those lists.
Consistency Models
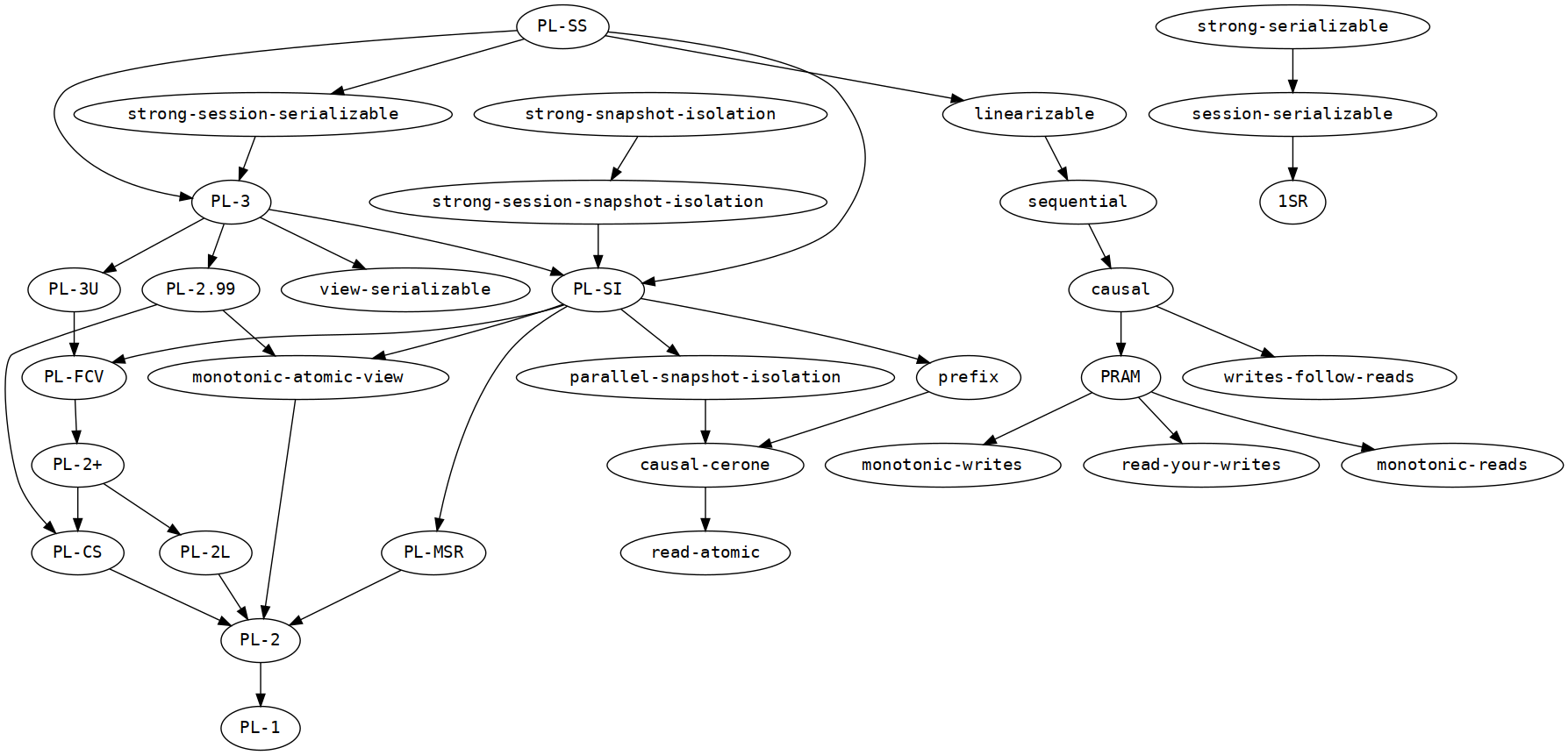
The following plot shows Elle's relationships between consistency models: an
arrow a -> b implies if a holds, then so does b. Sources for this
structure can be found in elle.consistency-model.
This plot shows the relationships between Elle's anomalies. An arrow a -> b
implies if we observe anomaly a in a history, then b exists in the history
as well.
Soundness
Elle can check for every non-predicate anomaly from Adya, Liskov, and O'Neil's Generalized Isolation Level Definitions. These include:
- G0: Write cycle.
- G1a: Aborted read.
- G1b: Intermediate read.
- G1c: Cyclic information flow.
- G-Single: Read skew.
- G2: Anti-dependency cycle.
There are additional anomalies (e.g. garbage reads, dirty updates, inconsistent version orders) available for specific checkers. Not all of these are implemented fully yet---see the paper for details.
- Internal Inconsistency: A transaction fails to observe its own prior reads/writes.
- Inconsistent Version Orders: Inference rules suggested a cyclic order of updates to a single key.
- Dirty Updates: A write promotes aborted state into committed state.
- Duplicate Writes: A write occurs more than once.
- Garbage Reads: A read observes a state which could not have been the product of any write.
In addition, Elle can infer transaction dependencies on the basis of process (e.g. session) or realtime order, allowing it to distinguish between, say, strict serializability and serializability.
For lists, Elle can infer a complete prefix of the Adya version order for a key based on a single read. For registers, Elle can infer version orders on the basis of the initial state, writes-follow-reads, process, and real-time orders.
When Elle claims an anomaly in an observable history, it specifically means that in any abstract Adya-style history which is compatible with that observed history, either a corresponding anomaly exists, or something worse happened---e.g. an aborted read. This is a natural consequence of testing real-world databases; if the database lies in just the right way, it might appear to exhibit anomalies which didn't actually happen, or mask anomalies which did. We limit the impact of this problem by being able to distinguish between many classes of reads, and sampling many anomalies---hoping that eventually, we get lucky and see the anomaly for what it "really is".
Completeness
Elle is not complete: it may fail to identify anomalies which were present in the system under test. This is a consequence of two factors:
- Elle checks histories observed from real databases, where the results of transactions might go unobserved, and timing information might not be as precise as one would like.
- Serializability checking is NP-complete; Elle intentionally limits its inferences to those solvable in linear (or log-linear) time.
In practice, we believe Elle is "complete enough". Indeterminacy is generally limited to unobserved transactions, or a small set of transactions at the very end of the history.
Performance
These plots show Elle's performance vs the Knossos linearizability checker, verifying histories of various lengths (l) and concurrencies (c), recorded from a simulated serializable snapshot isolated in-memory database. Lower is better.
In general, Elle checks real-world histories in a matter of seconds to minutes, rather than seconds to millennia. Where Knossos is often limited to a few hundred operations per history, Elle can handle hundreds of thousands of operations easily.
Knossos runtimes diverge exponentially with concurrency; Elle is effectively constant. There's a slight drop in runtime as concurrency increases, as more transactions abort due to conflicts. Knossos is also mildly superlinear in history length; Elle is effectively linear.
I haven't really optimized Elle yet---I'm sure it can be made faster with time. There are some spots (especially in inferring version orders from transaction graphs during register tests) which might be painful; I'll sand off rough edges as I go.
License
Elle is copyright 2019--2020 Jepsen, LLC and Peter Alvaro. The Elle library is available under the Eclipse Public License, version 2.0, or, at your option, GPL-2.0 with the classpath exception.
Thanks
Elle was inspired by conversations with Asha Karim, and Kit Patella (@mkcp) wrote the first prototype of the Elle checker.