The following introduces a small code snippet that calculates the count-bids as Grigory defined it.
Grigory's definition includes the following. Given we have a data.frame of companies and dates, we want to find dates that are 60 days apart, however, the catch is, that once a date is identified, this date blocks the next 60 dates, another entry at the 61$^{st}$ day will be counted again, regardless of other dates in between. Also, the first day is always chosen. The given example shows Abigail's Jewelry Inc and the five respective events. Of these five events the first is independent as it is the first event for the company (group) and is counted as 1. With a gap of 16 days, the second date is below the threshhold and is thus marked as dependent (counted as 0). The third event is still less than 60 days from the first counted with a difference of 31 days, as is the fourth event with 32 days. The last event has a distance of 74, therefore it is regarded as independent.
## comp date daydif
## 1: Abigail's Jewelry Inc 2009-05-15 16 days
## 2: Abigail's Jewelry Inc 2009-05-31 15 days
## 3: Abigail's Jewelry Inc 2009-06-15 1 days
## 4: Abigail's Jewelry Inc 2009-06-16 42 days
## 5: Abigail's Jewelry Inc 2009-07-28 NA days
The issue now is to create an algorithm that is able to identify these dates in the fastest way.
My humble approach is the following iei function that is used recursively (calling itself in the function). The function looks like this:
iei <- function(x) {
count <- c(1, rep(0, length(x) - 1))
count[(x - x[1]) > 60] <- 1
take <- cumsum(count) < 2
count_stay <- count[take]
x_new <- x[!take]
if (length(x_new) != 0) {
count_new <- iei(x_new)
} else {
count_new <- numeric(0)
}
c(count_stay, count_new)
}I know it looks complicated, therefore I will direclty dive into it and explain line by line.
iei <- function(x) {starts the iei function that takes x as an argument which is a vector of dates, for example 2000-01-02, 2000-03-01, 2000-05-19. "iei" stands for independent event identifier.
count <- c(1, rep(0, length(x) - 1))count is a vector with the same length as the input vector x. The first element is a 1, the other elements are zeros. The vector count will indicate if we choose a date as independent (1) or dependent (0).
count[(x - x[1]) > 60] <- 1set the elements in count that are more than 60 days away from the first element to 1, thus marking them independent (only from the first element of x).
take <- cumsum(count) < 2take is a vector containing boolean values (TRUE, or FALSE) if the date-values are covered by the first day's period of 60 days (dependent) including the first day.
So far the results would be the following given that our input is 2000-01-02, 2000-03-01, 2000-05-19:
x <- c("2000-01-02", "2000-03-01", "2000-05-19")
x <- as.Date(x)
# [1] "2000-01-02" "2000-03-01" "2000-05-19"
# Line 1:
count <- c(1, rep(0, length(x) - 1))
# [1] 1 0 0
# Line 2:
count[(x - x[1]) > 60] <- 1
# [1] 1 0 1
# Line 3:
take <- cumsum(count) < 2
# [1] TRUE TRUE FALSE
# Or in one data.frame:
# dates l1_count1 l2_count2 l3_csum l3_take
# 1 2000-01-02 1 1 1 TRUE
# 2 2000-03-01 0 0 1 TRUE
# 3 2000-05-19 0 1 2 FALSE
# where l1_count1 refers to line 1 and the first version of count
# l2_count2 refers to line 2 and the second version of count
# l3_csum refers to line 3 and the cumulative sum of count
# lastly l3_take refers to line 3 and the check if the cumulative sum is smaller than 2In the next steps we will keep only the first two as they are both dependent on the first date and rerun the whole function on the other value(s) where take == F.
count_stay <- count[take]
# count_stay
# [1] 1 0count_stay now contains all the values of countfor the values that are covered by the first event (dependent). These values are being kept in the variable for later use.
x_new <- x[!take]
# x_new
# [1] "2000-05-19"The value of x_new are all the values that are not covered by the first date in x (they are thus independent) and have to be reexamined by a recursive call to the function itself.
if (length(x_new) != 0) {
count_new <- iei(x_new)
} else {
count_new <- numeric(0)
}The if-clause iterates over the remaining date-values if there is another x_new in a recursive call (recursive because in the if-clause the function itself is called again on the remaining values. That means that the programm starts a new environment and sets x to x_new and iterates lines 1 thru 12). The else-clause is triggered in the last round and aborts the recursive loop. Note that numeric(0) is basically an empty element, thus concenating the empty element with another vector only returns the other vector.
c(count_stay, count_new)
}As a last step we concenate the old stay values with the new count values (as returned by the function itself). Note that the function kind of collapses from the top environment (the innermost call to the function itself returning a vector of 1s and 0s for the last dates not independent of the former dates) to the bottom environment, concenating the returing values along with it.
Coming back to our example of x = 2000-01-02, 2000-03-01, 2000-05-19 we expect a series of [1, 0, 1] as the difference between the first two dates is less than 60 days (returning a 1 for the first event, and a 0 for the second) and the third date is independent (i.e., more than 60 days apart). When we run the code we get
iei(x)## [1] 1 0 1
which is exactly what we expected.
Taking the data provided by Grigory from his Github page, we get the data that looks like this:
## id comp date
## 1: 1 Aaryn's Chocolate Inc 1997-07-18
## 2: 2 Aaryn's Chocolate Inc 1997-08-20
## 3: 3 Aaryn's Chocolate Inc 1997-08-21
## 4: 4 Abigail's Jewelry Inc 2009-05-15
## 5: 5 Abigail's Jewelry Inc 2009-05-31
## ---
## 996: 996 Zebulin's IceCream Inc 2008-01-16
## 997: 997 Zebulin's IceCream Inc 2008-01-22
## 998: 998 Zebulin's IceCream Inc 2008-02-06
## 999: 999 Zebulin's IceCream Inc 2008-02-09
## 1000: 1000 Zebulin's IceCream Inc 2008-03-03
As the function ``ieionly takes values per category, we can use the by-argument of thedata.table`-package to calculate the count variable:
dt[, count := iei(date), by = "comp"]
dt## id comp date count
## 1: 1 Aaryn's Chocolate Inc 1997-07-18 1
## 2: 2 Aaryn's Chocolate Inc 1997-08-20 0
## 3: 3 Aaryn's Chocolate Inc 1997-08-21 0
## 4: 4 Abigail's Jewelry Inc 2009-05-15 1
## 5: 5 Abigail's Jewelry Inc 2009-05-31 0
## ---
## 996: 996 Zebulin's IceCream Inc 2008-01-16 0
## 997: 997 Zebulin's IceCream Inc 2008-01-22 0
## 998: 998 Zebulin's IceCream Inc 2008-02-06 0
## 999: 999 Zebulin's IceCream Inc 2008-02-09 0
## 1000: 1000 Zebulin's IceCream Inc 2008-03-03 1
which gives a total of 394 independent events.
If we time the code, it takes roughly 0.2 seconds to calculate the counts over the 247 companies and the total of 1000 dates.
If we want to increase the computing speed, we have multiple options, I will briefly look into two options: optimising data structures and compiling the code.
The first tries to change the data structure so that it is able to run faster. One of the very primitive data types in R are integers (aka. whole numbers, i.e., 1, 2, 3, 10, 100, 1000, -1, -2, ...). So far we've used dates that are a bit more complex and thus require more computing time. Luckily it is very easy and fast for us to change the types of the variable. Using data.tables assignment operator := we get
dt[, date_int := as.integer(date)]
dt## id comp date date_int
## 1: 1 Aaryn's Chocolate Inc 1997-07-18 10060
## 2: 2 Aaryn's Chocolate Inc 1997-08-20 10093
## 3: 3 Aaryn's Chocolate Inc 1997-08-21 10094
## 4: 4 Abigail's Jewelry Inc 2009-05-15 14379
## 5: 5 Abigail's Jewelry Inc 2009-05-31 14395
## ---
## 996: 996 Zebulin's IceCream Inc 2008-01-16 13894
## 997: 997 Zebulin's IceCream Inc 2008-01-22 13900
## 998: 998 Zebulin's IceCream Inc 2008-02-06 13915
## 999: 999 Zebulin's IceCream Inc 2008-02-09 13918
## 1000: 1000 Zebulin's IceCream Inc 2008-03-03 13941
Under the hood, R takes the difference to an origin date which is usually either 1900-01-01, 1970-01-01 or 1904-01-01 (thanks Apple for this one!) in our case it is 1970-01-01 (which can be shown with as.integer(as.Date("1970-01-01")), which gives 0).
The second option compiles the code of iei to another function comp_iei that is easier for the computer to understand. This is easily done by using the compiler-package and its compfun-function like this
library(compiler)
comp_iei <- cmpfun(iei)We can call the optimized version as usual
dt[, count_int := iei(date_int), by = "comp"]
dt[, count_cmp := comp_iei(date), by = "comp"To compare the speeds of the different versions, we use the microbenchmark-package and the function of the same name. The functions are run 100 times and the summary statistics are computed for each run.
library(microbenchmark)
res_bench <- microbenchmark(
iei = dt[, count := iei(date), by = "comp"],
iei_int = dt[, count_comp := comp_iei(date), by = "comp"],
comp_iei = dt[, count_int := iei(date_int), by = "comp"],
comp_iei_int = dt[, count_int_comp := comp_iei(date_int), by = "comp"],
times = 100
)
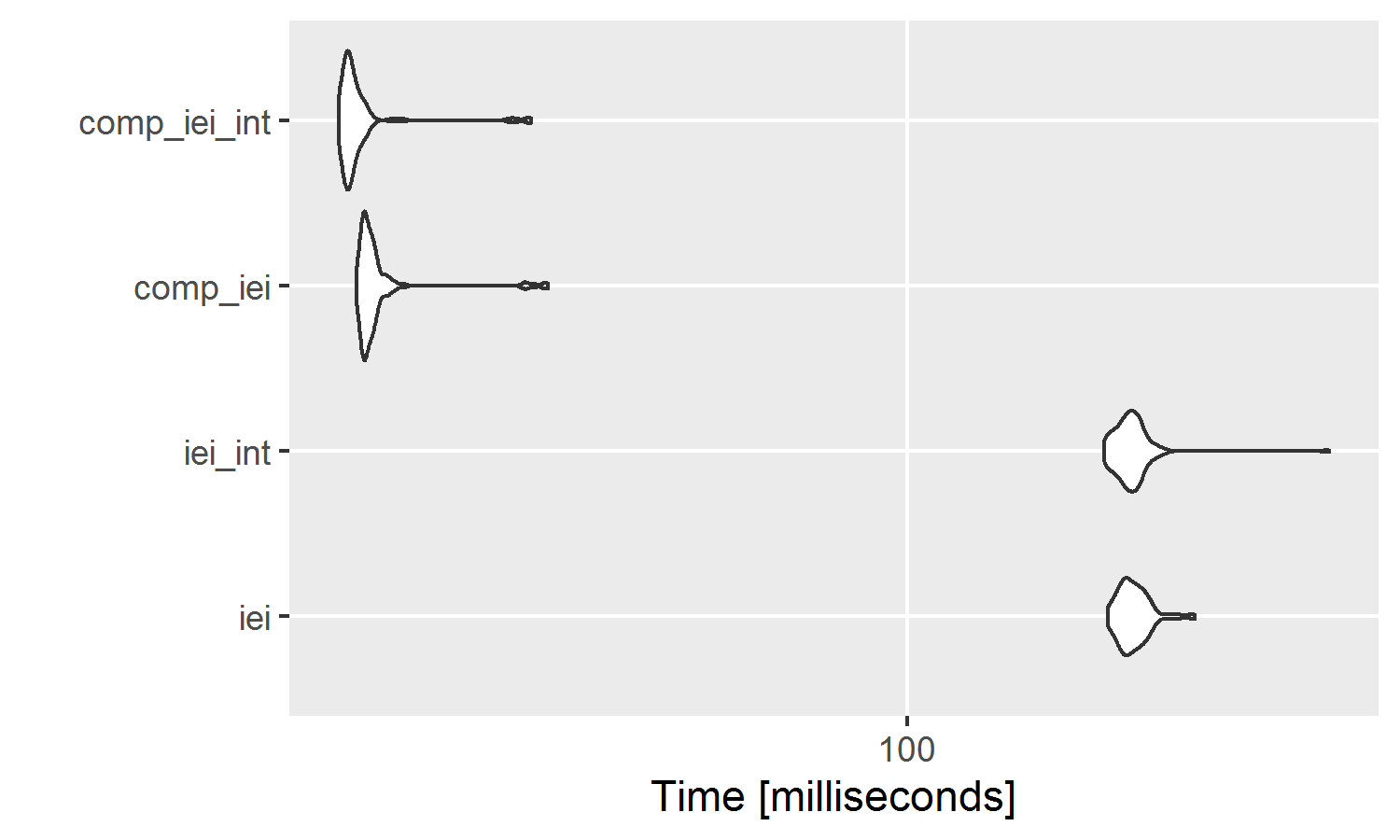
res_bench # prints the results as a table## Unit: milliseconds
## expr min lq mean median uq max
## iei 197.29162 207.03715 215.35822 212.75301 221.16470 264.49173
## iei_int 194.79227 205.65179 214.37802 212.27330 218.55623 416.39956
## comp_iei 15.50939 15.88958 16.83628 16.12319 16.51649 29.62734
## comp_iei_int 14.63254 14.96344 15.76969 15.17977 15.61436 27.98181
## neval cld
## 100 b
## 100 b
## 100 a
## 100 a
autoplot(res_bench) # plots the results using ggplot2We see that the compiled function using the integer dates takes roughly only 7% of the time the initial function took, reducing the average of the first function from 200 milliseconds down to 15 milliseconds.
Note that the speed is depending on the machine (I ran this code on a rather slow netbook with an Intel Celeron N3150 @ 1.60 GHz CPU, 4 GB of RAM on a 64 bit Windows 10 version). Rerunning the code on a Laptop with an Intel Core i7-3520M @ 2.90GHz with 8 GB of RAM on a 64 bit Windows 7 Professional I got results which where roughly 3 times faster at 54 milliseconds for the iei(date)-function and 3.8 milliseconds for the comp_iei(date_int).
all.equal(dt$count, dt$count_comp, dt$count_int, dt$count_int_comp)## [1] TRUE
For the math-savy, the algorithm can be explained like this:
where