Sam Greydanus | 2020
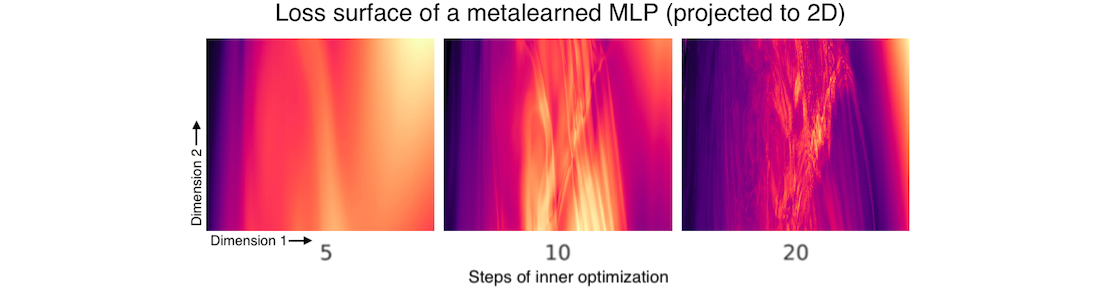
Quite a few functions are hard to optimize because they have many local minima. These functions often have "rough" loss surfaces: if you compute the analytic gradient at one point, then move a small distance away from that point and compute the gradient again, the two gradients look very different. One scenario where this happens is gradient-based metalearning (also called bilevel optimization). Here's an example from (Metz et al., 2019):
In situations like this one, it helps to smooth the loss surface, and thus the gradients, before optimization. Doing this points us towards regions of parameter space where the overall density of good solutions is higher. Once we get to these regions (eg. the upper right corner of the plots above), we can anneal the smoothing factor and zero in on a particularly good solution.
Any amount of noise involved in an optimization process helps to smooth the loss surface. Stochastic gradient descent is a good example: empirical results suggest that smaller batch sizes (more stochastic gradients) can actually improve generalization in neural networks. But I agree with Metz et al. 2019 when they claim that this isn't enough to stabilize metalearning. A more extreme alternative is to use evolution strategies as a stochastic, unbiased gradient estimator ("mutation rate" ~ "smoothness factor"). Many people would say that this is crazy...
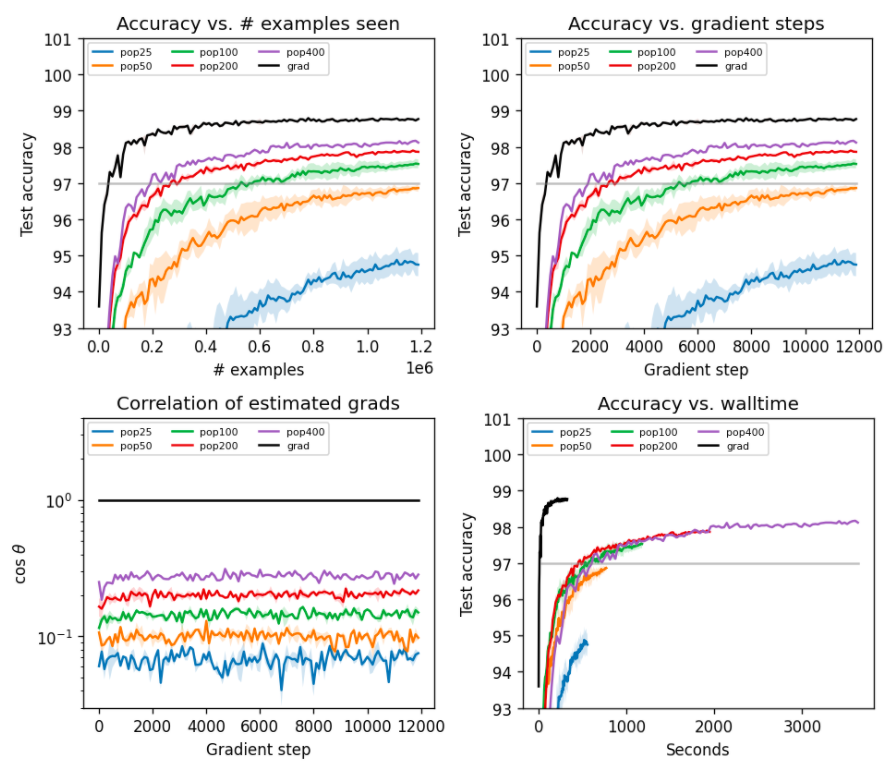
...but the purpose of this little library is to show otherwise. It consists of an ES gradient estimator and a series of benchmarks to evaluate how well it scales to high-dimensional neural network parameter spaces. Since one can never train too many MNIST classifiers, here are some results on MNIST:
The ultimate purpose of this ES gradient estimator is to optimize metalearning problems. Thus I am particularly interested in maximizing sample efficiency. After all, in metalearning, each "sample" is an entire learning process. These learning processes are extraordinarily expensive to compute.
- NumPy
- SciPy
- PyTorch