Osgood's surface (Osgood, 1949) was simulated by a Hebbian model. Osgood's surface summarises the behavioural data on paired associative learning. Speficially, it targets the situation in which participants learn two lists.
List1: Stimulus1 - Response1 -> List2: Stimulus2 - Response2
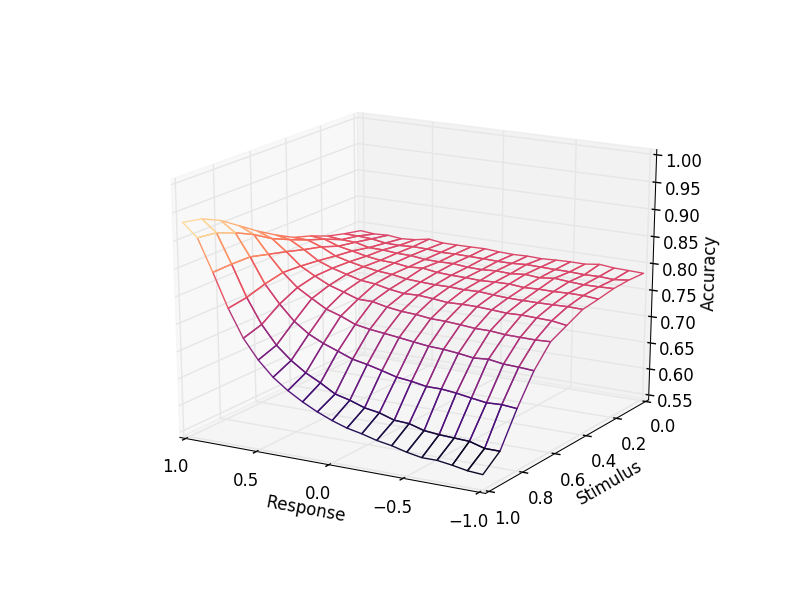
Osgood's surface is a surface on a three-dimensional space. In that three-dimensional space, the height shows transfer or retroaction. Roughly speaking, it corresponds to memory performance (Please read the original article!!). The width shows the similarity of stimuli (e.g., the similarity of Stimulus1 and Stimulus2). The length shows the similarity of responses (e.g., the similarity of Response1 and Response2).
For example, List1: apple - Toyota -> List2: orange - Porsche
In this case, the similarity of stimuli should be high (apple and orange are semantically related to each other) and that of responses also should be high.
In another case, say, List1: apple - Toyota -> List2: cigarette - Porsche
The similarity of stimuli (i.e., apple and cigarette) should be relatively low.
We can see how the two varibales, the similarity of stimuli and that of responses affect memory performance by Osgood surface.
Based on Farrell & Lewandowsky (2018), a hebbian model was coded. Try hebbian_osgood_surface.py and you will find that this Hebbian model works well!
The graph below shows the results of a simulation. Compare this graph with Osgood's graph!
That said, the values of the performance (Accuracy) for the Response of 0.0 to -1.0 do not fit with Osgood's surface well. One possible problem is the assumption on the similarity: I assume that the antagonistic response of r as -r. I might have to rethink about how the antagonistic response can be expressed in this hebbian model.
- numpy
- matplotlib
- mpl_toolkits
- scipy
Farrell, S., & Lewandowsky, S. (2018). Computational Modeling of Cognition and Behavior. Cambridge University Press. Osgood, C. E. (1949). The similarity paradox in human learning: A resolution. Psychological review, 56(3), 132.