mnist-vae
This repo has a few mnist classifiers (both simple 3 layer full connected and convolutional) as well as an implementation of autoencoders (both 'plain' and variational) and below the use of autoencoders for semi-supervised learning is explored.
MNIST
mnist_fc.py and mnist_conv.py represent simple MNIST classifiers. The former is a 3 layer fully connected network with 100 hidden units which achieves ~97.5% accuracy. The latter is a convolutional network with 2 convolutional layers (each with maxpooling), a 1024 unit fully connected hidden layer, and the final 10 unit output layer, achieving ~99.1% accuracy. The default training regime is to use early stopping when 3 consecutive epochs have passed with no improvement in accuracy when measured on the (5000 sample) validation set.
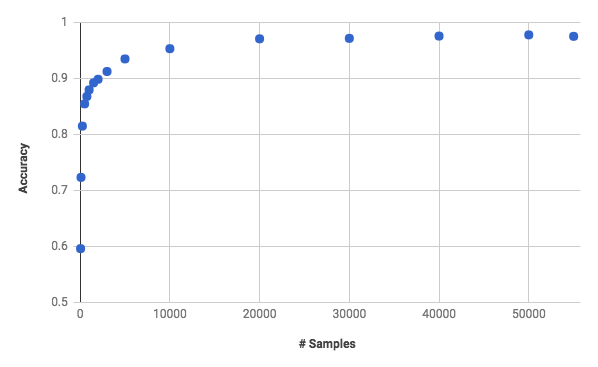
MNIST accuracy vs training samples
The MNIST dataset is split into training/validation/test samples of 55,000/5,000/10,000. For the fully connected network which achieves 97.5% on the full dataset, what is the sensitivity to training data size?
Remember that a random guess will give you 10% accuracy. You can see that 81% is achieved with only 250 samples and 90% with 2000. You need 27x the data to go from 90% to 97.5% with the simple network.
What about a world where you only have 2000 labeled samples but have another 53000 unlabeled samples? Can we somehow learn something in an unsupervised way from all 55000 digits that might help us to better than our 90% baseline? This is the goal of semi-supervised learning.
Autoencoders
An autoencoder is an unsupervised network architecture whereby the network is trained to reproduce the input, but is forced to do so by squeezing the data through a hidden layer with a drastically reduced number of dimensions. So for example a simple fully connected autoencoder might be 784 input -> 512 hidden -> 20 hidden -> 512 hidden -> 784 output. Training the network is the same as in the supervised case but you use the input as the label (your x,y training pair is really x,x). In this way you can view the autoencoder as a "domain specific lossy compressor" in that whatever those 20 hidden values are we can use them to reconstruct the input (though not perfectly). The 20 hidden values are referred to as "latent variables" because the hope is that the network learns the 20 underlying factors that make up the myriad of ways to handwrite the 0-9 digits. Such latent variables might be the class (0-9), the slant or boldness of the stroke, etc. Below you can see how good of a reconstruction you can get with 2, 5, and 20 dimensions (originals are on the left, reconstructions on the right).
The quality of the reconstruction with just 2 dimensions is impressive, and with 20 we get a reconstruction so good you probably wouldn't notice if the original and reconstructed versions were swapped.
Variational Autoencoders
The naive form of autoencoder described above sometimes apparently has a tendency to learn poor latent encodings which don't generalize well. Enter the "variational autoencoder" (or VAE). There are many great articles (see below in resources) that describe them, but the basic "trick" is to introduce randomization in the latent code. In particular, instead of learning a single latent encoding (say of 20 dimensions), you learn 2 of them, and you combine them into a single 20 dimensional value to be used for decoding/reconstruction of the object. In particular the 2 latent variables are used as the mean and standard deviation of a random noise signal. The intuition here (which I admit is fuzzy for me) is that instead of letting the reconstruction see the exact latent encoding that was derived from the exact object, which could lead to odd latent encodings where the items are not suitably "spaced out" in the latent space, you basically "jiggle around" the values so the latent code is forced to have enough 'robustness' to properly decode them. For example it will make sure the latent encoding doesn't put the 1's uneessarily close to the 7's in latent space. This smells to me like a form of regularization.
Below are reconstructions with a VAE for 2, 5, and 20 dimensions. Note that it is not as sharp, perhaps due to the randomization.
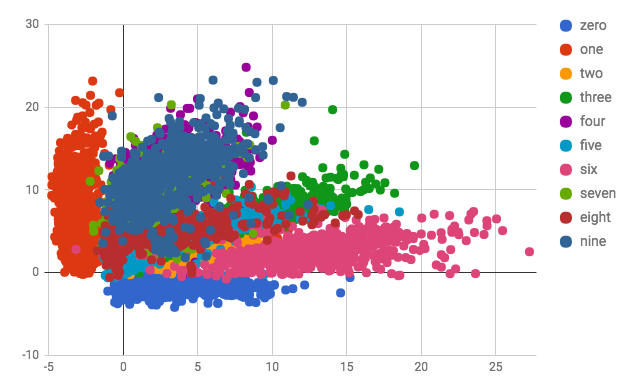
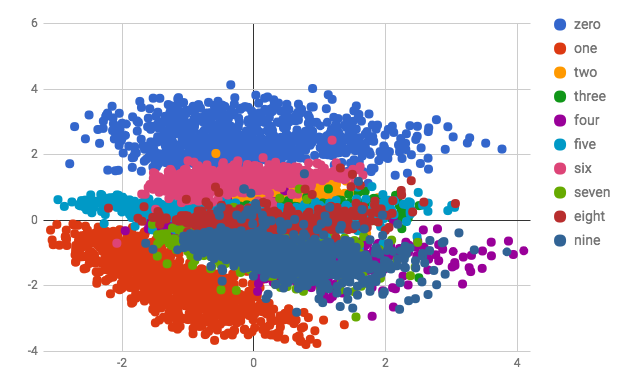
Visualizing MNIST Digits in 2-D Latent Space
Below is a scatter plot of the 10,000 training samples from MNIST embedded in a 2-D space. The first plot shows the plain autoencoder version and the second shows the VAE. Note that with only 2 dimensions the clusters have severe overlap. Both encodings have 4's and 9's heavily overlapped, which is reflected in the above reconstructions which shows a 4 being reconstructed as a fuzzy 9.
Semi-Supervised Learning
So what if instead of 55,000 labeled training samples, we only had 2,000 lateled training samples and 53,000 unlabeled samples. Can we generate a (for example) 20 dimensional latent encoding of MNIST digits learned in an unsupervised way with an autoencoder, and then train on that using 2,000 labeled samples? Will that latent encoding give us a net better result than the 90% we get with just training on 2,000 labeled images? To run the test using an autoencoder run python mnist_conv_vae.py, add the --vae flag to run a VAE. You will see both autoencoders get a ~93.5% accuracy, which recovers about half of the accuracy lost when we went to 2,000 labeled samples. This is an impressive result and gives some feeling for why researchers and practitioners are excited about the potential to improve training through additional unlabeled data.
It is not immediately clear to me why the VAE doesn't outperform the autoencoder, in fact nothing in my comically naive exploration has not clearly demonstrated the value of VAEs over "plain autoencoders", but this is of course my own ignorance (or possible bugs). VAEs seem to dominate the literature so perhaps there is a different set of circumstances where they shine (or again, bugs in my impl may explain all). If you have any ideas let me know by filing a bug!
Resources
Auto-Encoding Variational Bayes The original D.P. Kingma paper introducing the VAE.
Tutorial on Variational Autoencoders Carl Doersch's oft cited explanation of VAEs.
Variational Autoencoders Explained Kevin Frans nice explan of VAEs with Tensorflow code.
Introducing Variational Autoencoders Another good explanation and sample code explaining VAEs