guillermo-navas-palencia/cprior

Fast Bayesian A/B and Multivariate testing.

CPrior

CPrior has functionalities to perform Bayesian statistics and running A/B and multivariate testing. CPrior includes several conjugate prior distributions and has been developed focusing on performance, implementing many closed-forms in terms of special functions to obtain fast and accurate results, avoiding Monte Carlo methods whenever possible.

Website: http://gnpalencia.org/cprior/

Installation

To install the current release of CPrior on Linux/Windows:

pip install cprior

For different OS and/or custom installations, see http://gnpalencia.org/cprior/getting_started.html.

Dependencies

CPrior has been tested with CPython 3.5, 3.6 and 3.7. It requires:

• mpmath 1.0.0 or later. Website: http://mpmath.org/
• numpy 1.15.0 or later. Website: https://www.numpy.org/
• scipy 1.0.0 or later. Website: https://scipy.org/scipylib/
• pytest
• coverage

Testing

Run all unit tests

python setup.py test

Examples

Example: run experiment

A Bayesian multivariate test with control and 3 variants. Data follows a Bernoulli distribution with distinct success probability.

1. Generate control and variant models and build experiment. Select stopping rule and threshold (epsilon).

from scipy import stats
from cprior.models.bernoulli import BernoulliModel
from cprior.models.bernoulli import BernoulliMVTest
from cprior.experiment.base import Experiment

modelA = BernoulliModel(name="control", alpha=1, beta=1)
modelB = BernoulliModel(name="variation", alpha=1, beta=1)
modelC = BernoulliModel(name="variation", alpha=1, beta=1)
modelD = BernoulliModel(name="variation", alpha=1, beta=1)

mvtest = BernoulliMVTest({"A": modelA, "B": modelB, "C": modelC, "D": modelD})

experiment = Experiment(name="CTR", test=mvtest, stopping_rule="probability_vs_all",
                        epsilon=0.99, min_n_samples=1000, max_n_samples=None)

2. See experiment description

experiment.describe()

=====================================================
  Experiment: CTR
=====================================================
    Bayesian model:                bernoulli-beta
    Number of variants:                         4

    Options:
      stopping rule            probability_vs_all
      epsilon                             0.99000
      min_n_samples                          1000
      max_n_samples                       not set

    Priors:

         alpha  beta
      A      1     1
      B      1     1
      C      1     1
      D      1     1
  -------------------------------------------------

3. Generate or pass new data and update models until a clear winner is found. The stopping rule will be updated after a new update.

with experiment as e:
    while not e.termination:
        data_A = stats.bernoulli(p=0.0223).rvs(size=25)
        data_B = stats.bernoulli(p=0.1128).rvs(size=15)
        data_C = stats.bernoulli(p=0.0751).rvs(size=35)
        data_D = stats.bernoulli(p=0.0280).rvs(size=15)

        e.run_update(**{"A": data_A, "B": data_B, "C": data_C, "D": data_D})

    print(e.termination, e.status)

True winner B

4. Reporting: experiment summary

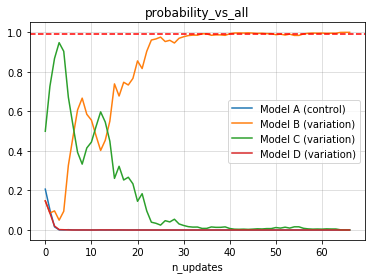
experiment.summary()

5. Reporting: visualize stopping rule metric over time (updates)

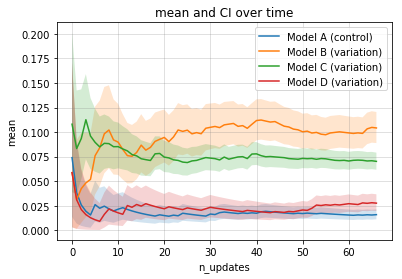
experiment.plot_metric()

6. Reporting: visualize statistics over time (updates)

experiment.plot_stats()

Example: basic A/B test

A Bayesian A/B test with data following a Bernoulli distribution with two distinct success probability. This example is a simple use case for CRO (conversion rate) or CTR (click-through rate) testing.

from scipy import stats

from cprior.models import BernoulliModel
from cprior.models import BernoulliABTest

modelA = BernoulliModel()
modelB = BernoulliModel()

test = BernoulliABTest(modelA=modelA, modelB=modelB)

data_A = stats.bernoulli(p=0.10).rvs(size=1500, random_state=42)
data_B = stats.bernoulli(p=0.11).rvs(size=1600, random_state=42)

test.update_A(data_A)
test.update_B(data_B)

# Compute P[A > B] and P[B > A]
print("P[A > B] = {:.4f}".format(test.probability(variant="A")))
print("P[B > A] = {:.4f}".format(test.probability(variant="B")))

# Compute posterior expected loss given a variant
print("E[max(B - A, 0)] = {:.4f}".format(test.expected_loss(variant="A")))
print("E[max(A - B, 0)] = {:.4f}".format(test.expected_loss(variant="B")))

The output should be the following:

P[A > B] = 0.1024
P[B > A] = 0.8976
E[max(B - A, 0)] = 0.0147
E[max(A - B, 0)] = 0.0005