Aim of the Game:
The goal of "Shut the Box" is to flip down all numbers from 1 to 12.
Game Materials:
- A "Shut the Box" game board with numbers from 1 to 12.
- Two dice with faces numbered 1 to 6.
Game Rules:
-
At the start of the game, all numbers on the game board are flipped up.
-
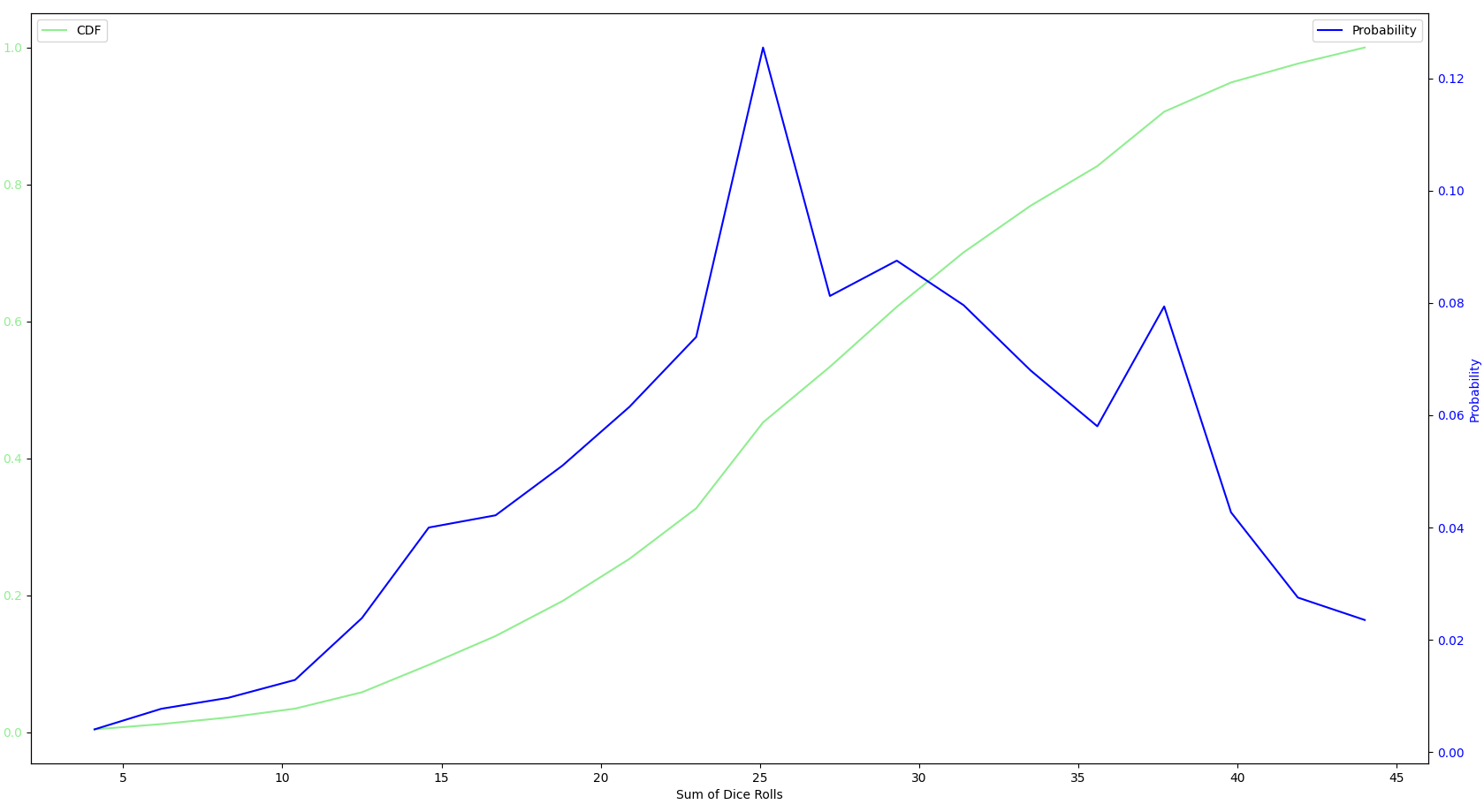
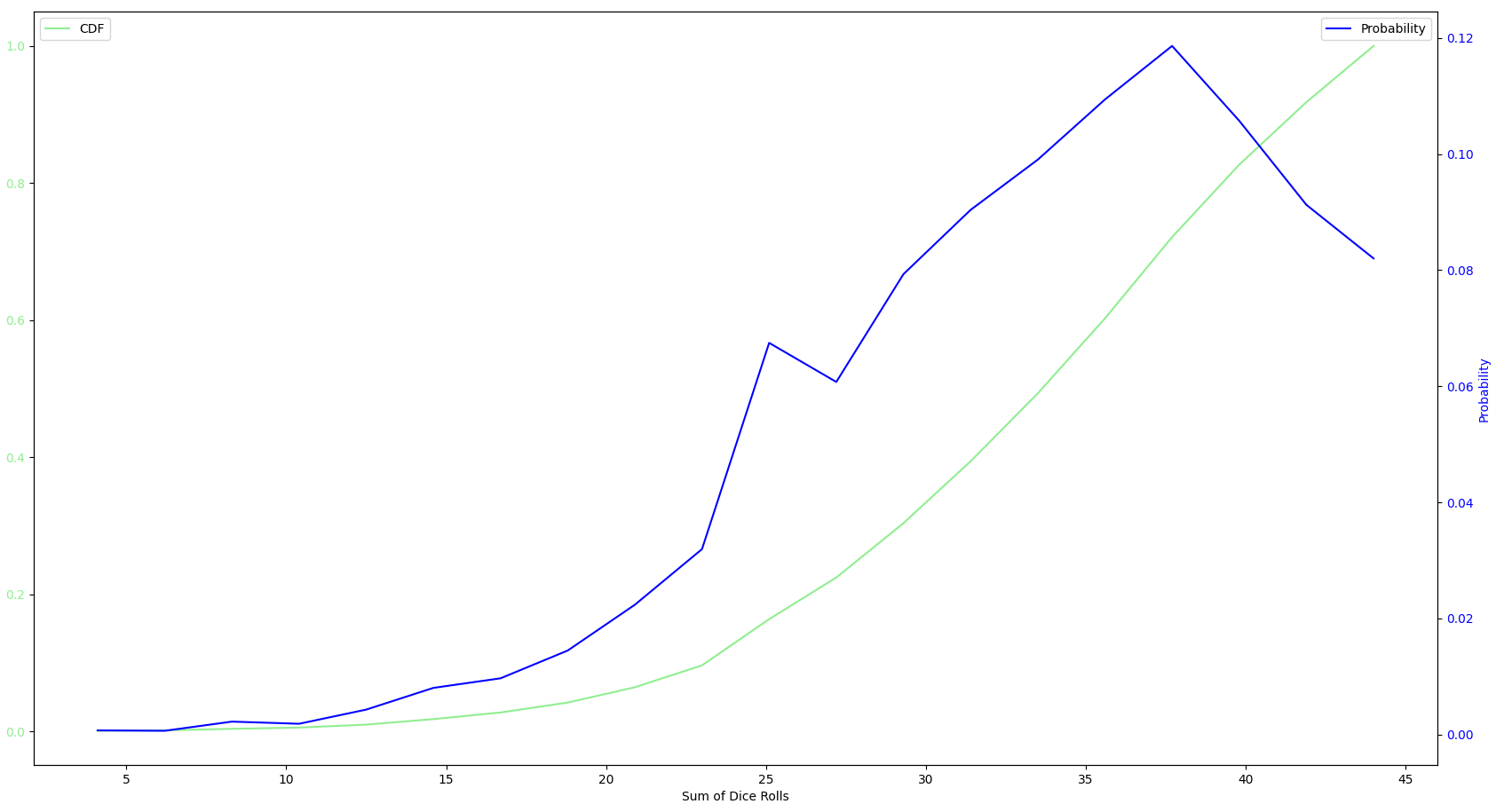
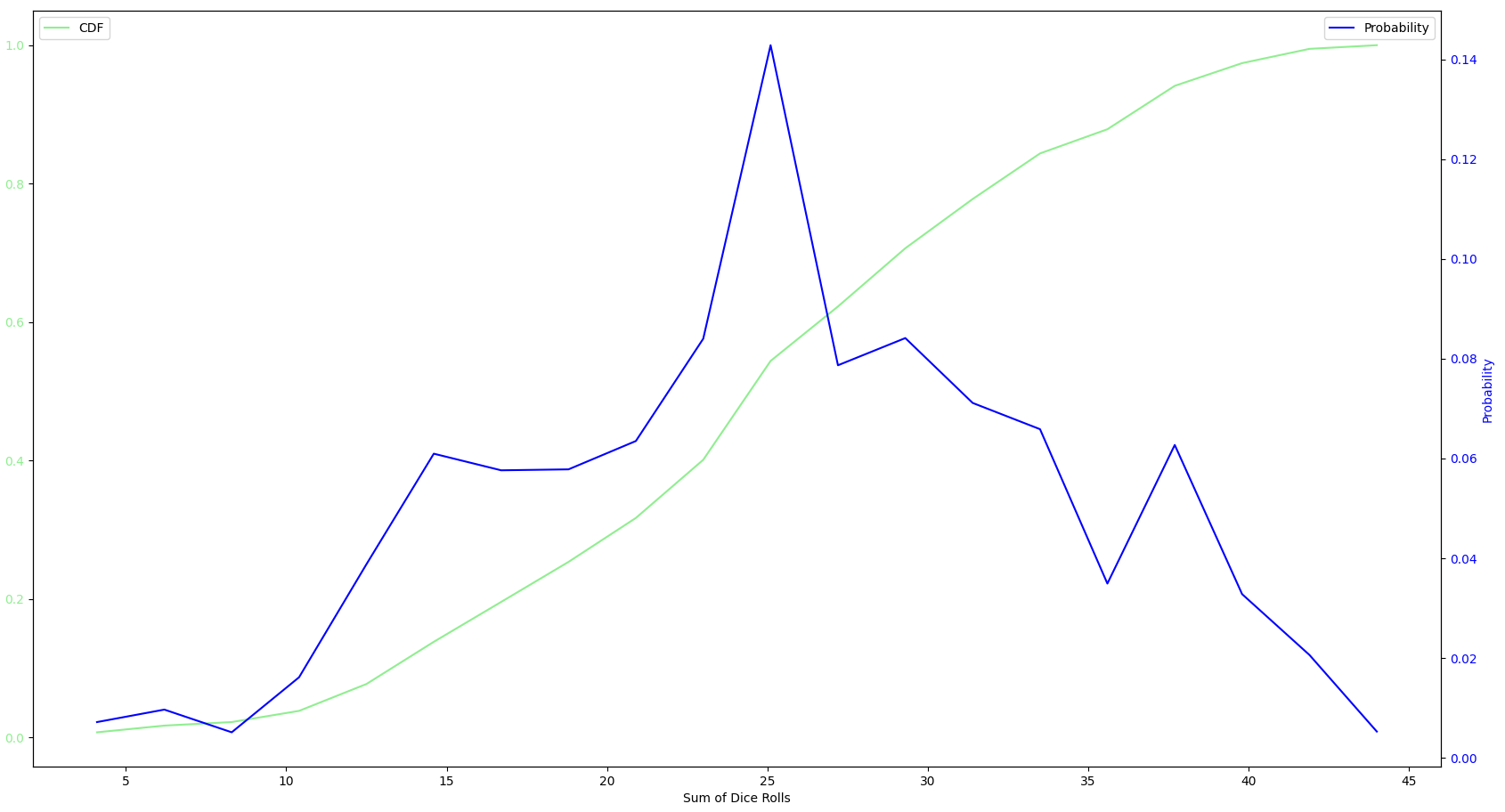
A player rolls both dice and adds the numbers rolled.
-
The player then selects any combinations of flipped down numbers on the game board whose sum equals the sum of the dice rolls (FOR THIS SIMULATION MAX OF 2).
-
If a player cannot find any combinations of flipped down numbers that equal the sum of the dice rolls, their turn ends.
-
The player repeats steps 2-4 until all numbers on the game board have been flipped down or no more moves are possible.
-
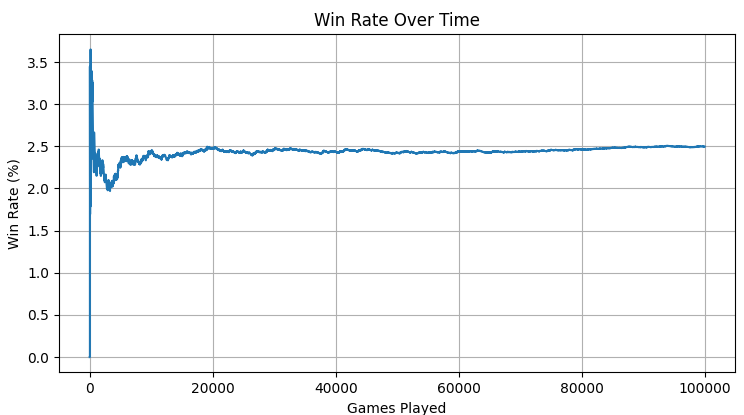
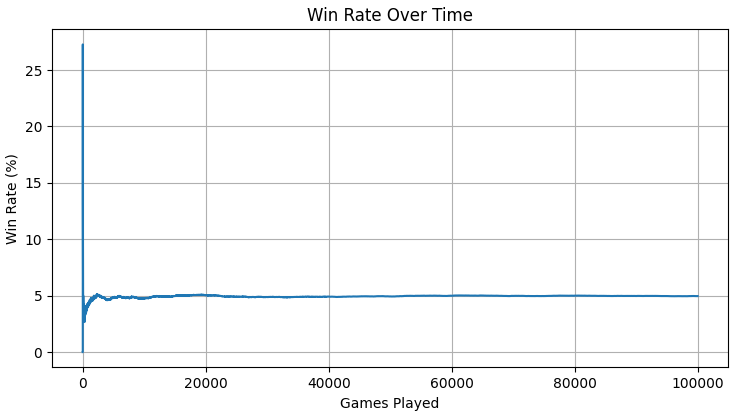
If all numbers on the game board have been flipped down, the player wins. Otherwise, the sum of the remaining flipped up numbers is counted as their score.
-
Winner:
The player with the lowest score wins. In a variation of the game, players can also attempt to improve their scores from round to round.
I am interested in comparing various strategies for playing "Shut the Box" using simulations.
Objective:
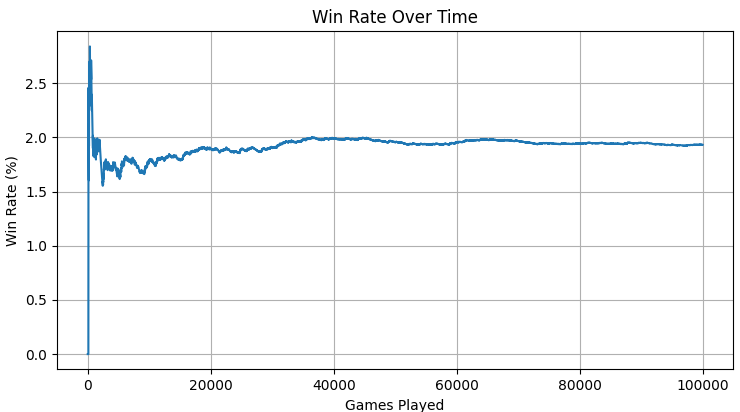
The objective of the simulation is to evaluate the effectiveness of different strategies in achieving the lowest score possible in "Shut the Box".
Strategies:
I will implement and compare several strategies, such as:
- Random selection of numbers to flip down.
- Greedy strategy: Always choosing the combination that flips down the highest possible number of digits.
- Optimized algorithms: Implementing more sophisticated algorithms based on game theory or dynamic programming to determine the best moves.
Simulation Setup:
- Simulate multiple games for each strategy.
- Record the scores achieved by each strategy in each game.
- Analyze the distribution of scores and compare the performance of different strategies.
Highest Value (greedy) - Player flips down a combination with the highest number possible(e.g 9 is prefered over 4/5)
Lowest Value - Player flips down a combination with the lowest number possible (e.g 1/2 is prefered over 3)
Coming Soon