Dichotomy Minimization Method

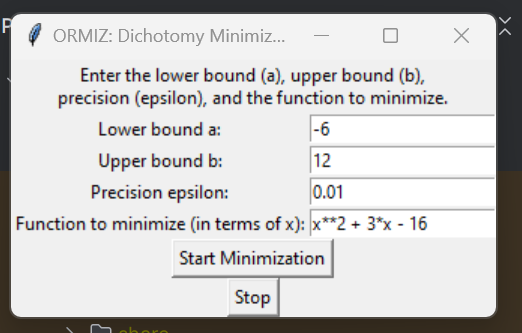
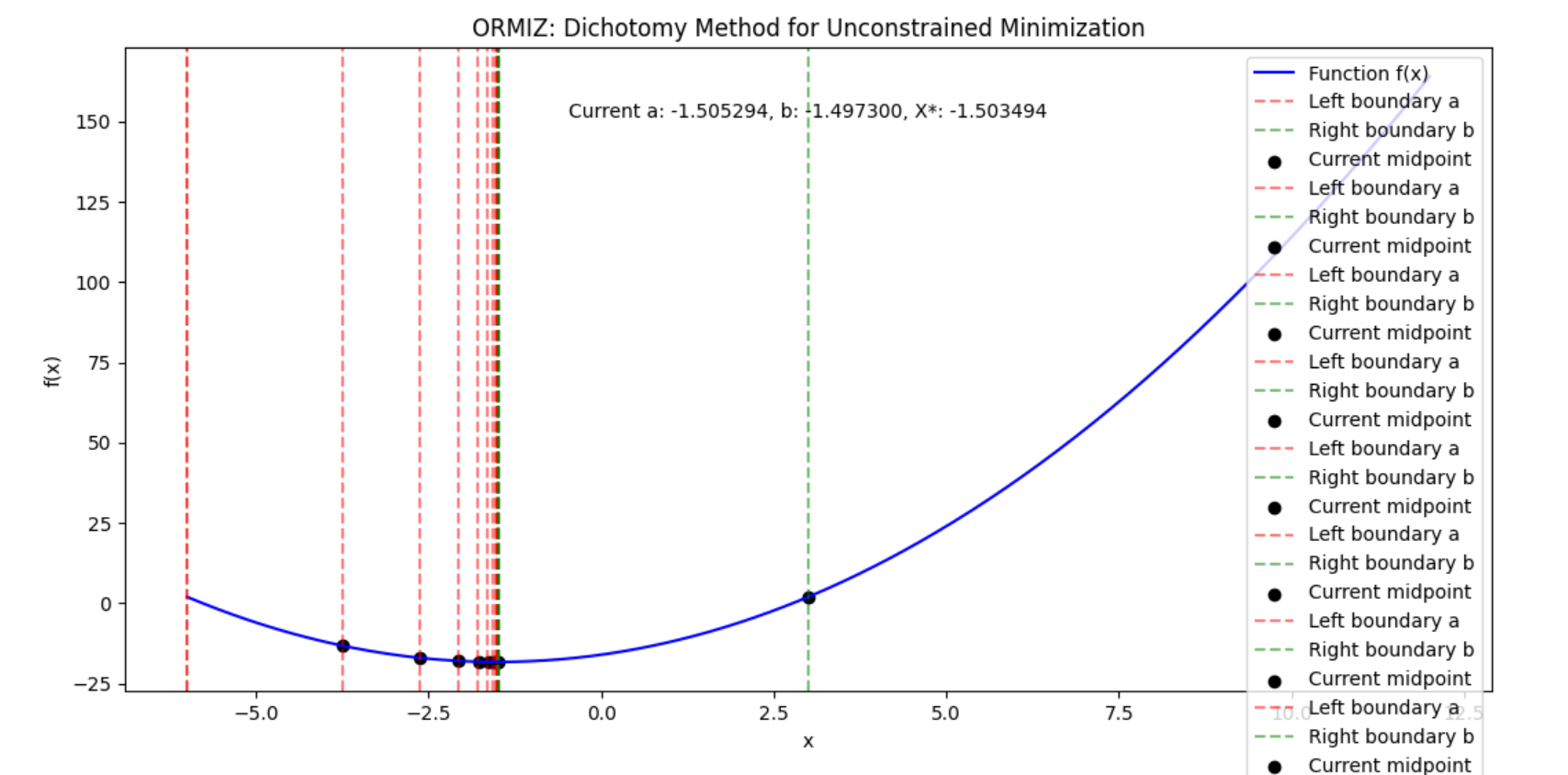
This project implements the Dichotomy Method for unconstrained minimization of a given function. The program is designed with a user-friendly interface and provides live graph updates as the minimization process progresses.

Features

Interactive User Interface: Users can input the lower bound (a), upper bound (b), precision (epsilon), and the function they wish to minimize.
Dynamic Graph Visualization: As the minimization process runs, it updates the graph in real-time, showing the function, the current interval, and the midpoint.
Editable Function: Users can enter and modify the function to be minimized directly through the interface.
Process Interruption: The minimization process can be stopped at any point without losing the current result.
Warnings and Suggestions: If the process is running too many iterations or the epsilon is too small, the user will be prompted to make adjustments.
Graphical Representation of Iterations: The graphical output includes live updates of the interval narrowing, with the boundaries and midpoint plotted at each step.

How to Use

Install the Required Libraries: You need the following Python libraries to run the program:
```
pip install tkinter matplotlib numpy
```
Running the Program:
- Clone the repository:
```
git clone https://github.com/hallame/dichotomy_method
cd dichotomy_method
```
- Run the Python script:
```
python main.py
```
- Alternatively, if you have the .exe file, simply double-click to run the program on a Windows machine. No installation required.

Input Values

Lower Bound (a): The left endpoint of the interval where the function is defined. It must be less than the upper bound.
Upper Bound (b): The right endpoint of the interval. It must be greater than the lower bound.
Precision (epsilon): The desired accuracy of the minimization. A smaller value will lead to a more accurate result but may take longer to compute.
Function: The mathematical function to minimize. Enter it as a Python expression (e.g., x**2 + 3*x + 3). The function must be unimodal in the interval [a, b] for the method to work correctly.

Output

The program provides graphical output showing the function curve and the iterative process of finding the minimum. The graph updates in real-time, displaying:
- The function being minimized in blue.
- Vertical dashed lines representing the current interval boundaries (red for lower bound and green for upper bound).
- A black dot marking the current midpoint where the function is evaluated.
At the end of the minimization, a pop-up window displays the approximate minimum value found, along with the corresponding (x) value.

Example

For example, to minimize the function:

[ f(x) = x^2 + 3x + 3 ]

Analytical Solution:

To find the minimum of the function ( f(x) = x^2 + 3x + 3 ), we first take its derivative:

[ f'(x) = 2x + 3 ]

Set the derivative to zero to find the critical points:

[ 2x + 3 = 0 \quad \Rightarrow \quad x = -\frac{3}{2} = -1.5 ]

At ( x = -1.5 ), we compute the function value:

[ f(-1.5) = (-1.5)^2 + 3(-1.5) + 3 = 2.25 - 4.5 + 3 = 0.75 ]

Thus, the minimum value is approximately ( f(x) = 0.75 ) at ( x = -1.5 ).

hallame/dichotomy_method