/matlab-CG

Conjugate Gradient method (CG)

Primary LanguageMATLAB

CG method

Reference

Conjugate Gradient Method (ENG)

켤레기울기법 (KOR)

Conjugate Gradient Method (CG)

The conjugate gradient method is an algorithm for the numerical solution of particular systems of linear equations, namely those whose matrix is symmetric and positive-definite. The conjugate gradient method is often implemented as an iterative algorithm, applicable to sparse systems that are too large to be handled by a direct implementation or other direct methods such as the Cholesky decomposition.

Description of the problem

Suppose we want to solve the system of linear equations

    (P1) A * x   = b    : matrix ver.

or,

    (P2) A( x )  = b    : function ver.

for the vector x, where the known n x n matrix A is symmetric (i.e., A^T = A), positive-definite (i.e., x^T A x > 0 for all non-zero vectors x in R^n), and real, and b is known as well. We denote the unique solution of this system by x^*.

The basic iteration CG for solving problem (matrix ver.)

function [x] = conjgrad(A, b, x)
    r = b - A * x;
    p = r;
    rsold = r' * r;

    for i = 1:length(b)
        Ap = A * p;
        alpha = rsold / (p' * Ap);
        x = x + alpha * p;
        r = r - alpha * Ap;
        rsnew = r' * r;
        if sqrt(rsnew) < 1e-10
            break;
        end
        p = r + (rsnew / rsold) * p;
        rsold = rsnew;
    end
end

The basic iteration CG for solving problem (function ver.)

function [x] = conjgrad(A, b, x, N)
    r = b - A ( x );
    p = r;
    rsold = r(:)' * r(:);

    for i = 1:N
        Ap = A ( p );
        alpha = rsold / (p(:)' * Ap(:));
        x = x + alpha * p;
        r = r - alpha * Ap;
        rsnew = r(:)' * r(:);
        if sqrt(rsnew) < 1e-10
            break;
        end
        p = r + (rsnew / rsold) * p;
        rsold = rsnew;
    end
end

Example

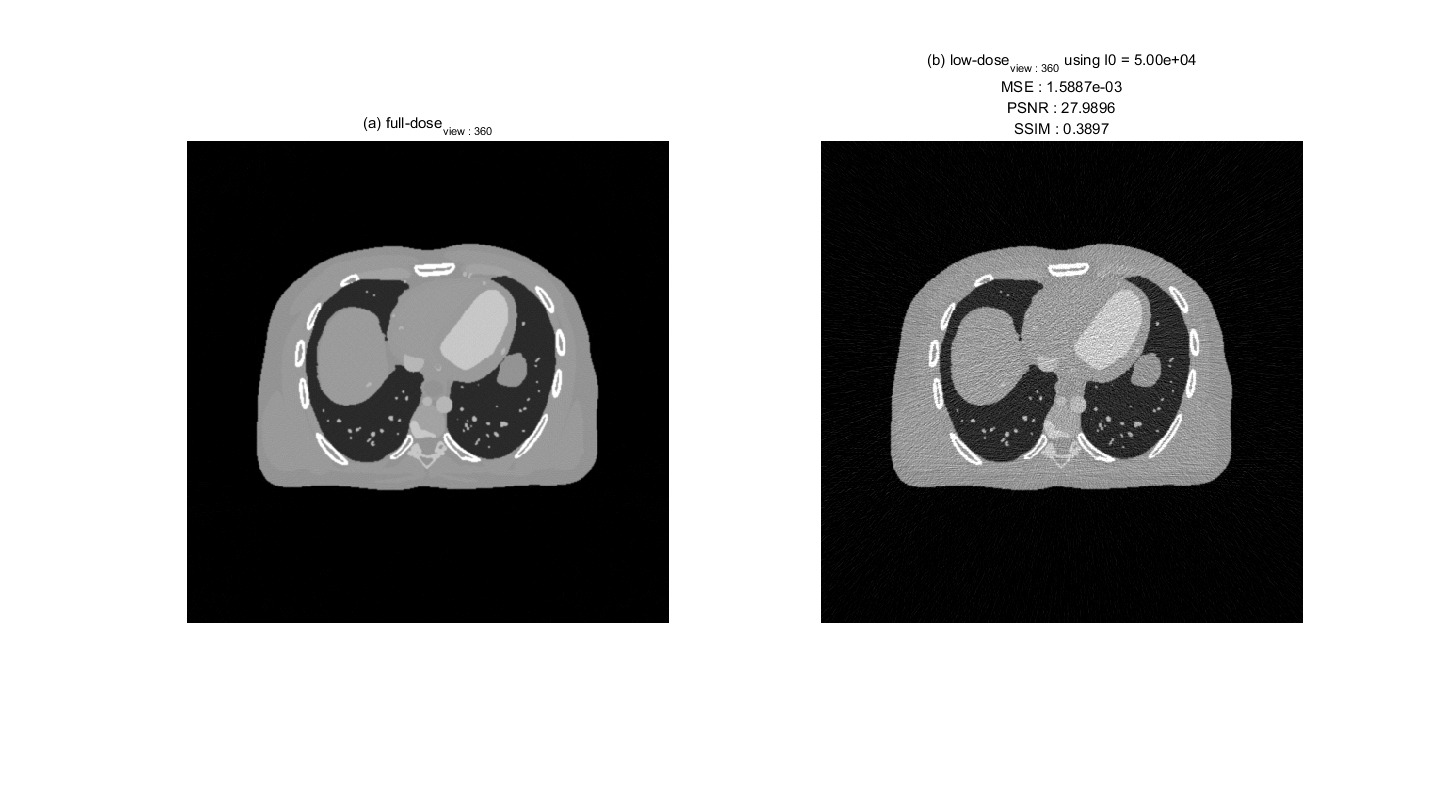
Problem definition

In X-ray computed tomography (CT) system, radiation exposure is critical limitation. To reduce the radiation exposure, X-ray CT system uses a low-dose X-ray source. The low-dose X-ray source generate severe poison noise when X-ray photon are measured at X-ray detector, then a reconstruction image using low-dose measurement is too noisy to diagnosis diseases by doctor. Below image shows (a) full-dose image and (b) low-dose image, respectively.

alt text

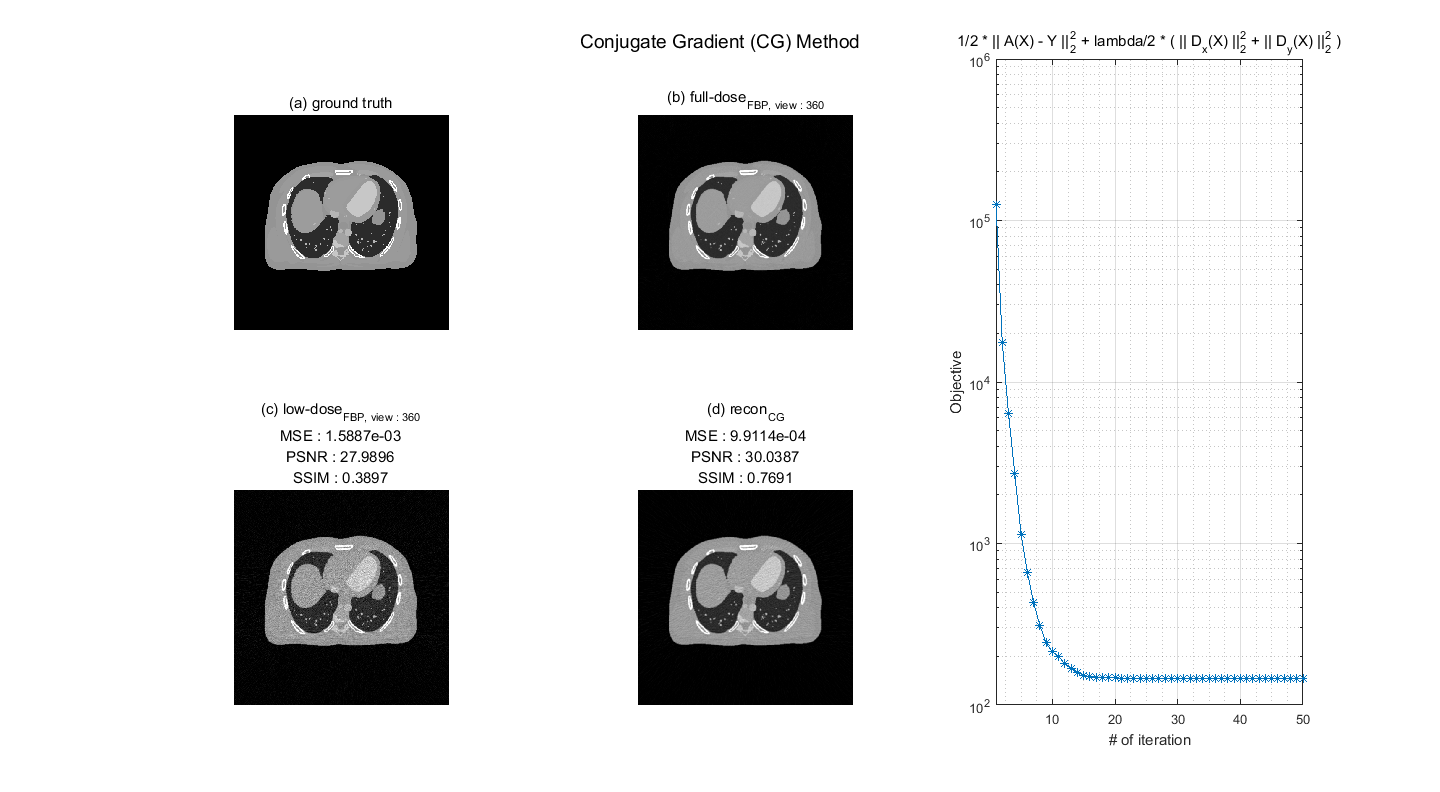
To reduce the noise, objective function with total variation (TV) regularization can be formulated as follows:

$$L(\textrm{x}) = \frac{1}{2} || \textrm{y} - A\textrm{x} ||_2^2 + \frac{\lambda}{2} ( ||D_x(\textrm{x})||_2^2 + ||D_y(\textrm{x})||_2^2 ),$$

where $\textrm{y}$ is measurement and $\textrm{x}$ defines reconstruction image (denoised image). $A$ is system operator (in this case, it is defined as CT system operator, called by radon transform). $D_x$ and $D_y$ are differential operators along x-axis and y-axis, respectively.

In above equation, since each terms is quadratic function, an optimal point of $\textrm{x}$ is $\frac{d}{d\textrm{x}}L(x)=0$:

$$-A^T (\textrm{y} - A\textrm{x})+ \lambda( D_x^T D_x(\textrm{x}) + D_y^T D_y(\textrm{x})) = 0,$$

$$A^TA(\textrm{x}) + \lambda( D_x^T D_x(\textrm{x}) + D_y^T D_y(\textrm{x})) = A^T\textrm{y},$$

$$A^TA + \lambda( D_x^T D_x + D_y^T D_y) = A^T\textrm{y}.$$

To match the CG formula, $[A^TA + \lambda( D_x^T D_x + D_y^T D_y)]$ is defined as $A_{cg}$ and $A^T\textrm{y} = b$, then

$$\therefore A_{cg}(\textrm{x}) = b.$$

Now, above equation form $A_{cg}(\textrm{x}) = b$ is exactly matched with CG equation form $A(x)=b$. Using above reordered formula, optimal point $\textrm{x}^*$ of $L(\textrm{x})$ can be found.

Results

alt text