Demo Site 哔哩哔哩 | 大白话AI | 扩散模型 (Chinese)
Video Explaination(Chinese)
-
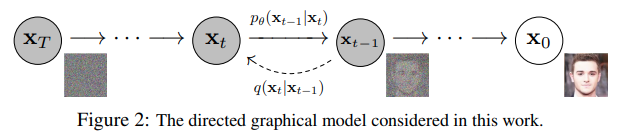
$q$ - a fixed (or predefined) forward diffusion process of adding Gaussian noise to an image gradually, until ending up with pure noise -
$p_θ$ - a learned reverse denoising diffusion process, where a neural network is trained to gradually denoise an image starting from pure noise, until ending up with an actual image.
Both the forward and reverse process indexed by
This process is a markov chain,
-
$β_t$ is not constant at each time step$t$ . In fact one defines a so-called "variance schedule", which can be linear, quadratic, cosine, etc.
-
$ϵ_{t}$ Gaussian noise, sampled from standard normal distribution.
Define
Because $N(\mu_{1},\sigma_{1}^{2}) + N(\mu_{2},\sigma_{2}^{2}) = N(\mu_{1}+\mu_{2},\sigma_{1}^{2} + \sigma_{2}^{2})$
$x_t = \sqrt{a_{t}a_{t-1}}\times x_{t-2} + \sqrt{1-a_{t}a_{t-1}}\times ϵ$ $x_t = \sqrt{a_{t}a_{t-1}a_{t-2}}\times x_{t-3} + \sqrt{1-a_{t}a_{t-1}a_{t-2}}\times ϵ$ $x_t = \sqrt{a_{t}a_{t-1}a_{t-2}a_{t-3}...a_{t-(k-2)}a_{t-(k-1)}}\times x_{t-k} + \sqrt{1-a_{t}a_{t-1}a_{t-2}a_{t-3}...a_{t-(k-2)}a_{t-(k-1)}}\times ϵ$ $x_t = \sqrt{a_{t}a_{t-1}a_{t-2}a_{t-3}...a_{2}a_{1}}\times x_{0} + \sqrt{1-a_{t}a_{t-1}a_{t-2}a_{t-3}...a_{2}a_{1}}\times ϵ$
$$\bar{a}{t} := a{t}a_{t-1}a_{t-2}a_{t-3}...a_{2}a_{1}$$
$$ q(x_{t}|x_{0}) = \frac{1}{\sqrt{2\pi } \sqrt{1-\bar{a}{t}}} e^{\left ( -\frac{1}{2}\frac{(x{t}-\sqrt{\bar{a}{t}}x_0)^2}{1-\bar{a}{t}} \right ) } $$
Because
|
|
~ |
|
|
|
~ |
|
|
|
~ |
|
$$ q(x_{t-1}|x_{0}) = \frac{1}{\sqrt{2\pi } \sqrt{1-\bar{a}{t-1}}} e^{\left ( -\frac{1}{2}\frac{(x{t-1}-\sqrt{\bar{a}{t-1}}x_0)^2}{1-\bar{a}{t-1}} \right ) } $$
$$ q(x_{t}|x_{0}) = \frac{1}{\sqrt{2\pi } \sqrt{1-\bar{a}{t}}} e^{\left ( -\frac{1}{2}\frac{(x{t}-\sqrt{\bar{a}{t}}x_0)^2}{1-\bar{a}{t}} \right ) } $$
$$ \frac{ q(x_{t}|x_{t-1},x_{0})\times q(x_{t-1}|x_0)}{q(x_{t}|x_0)} = \left [
\frac{1}{\sqrt{2\pi} \sqrt{1-a_{t}}} e^{\left ( -\frac{1}{2}\frac{(x_{t}-\sqrt{a_t}x_{t-1})^2}{1-a_{t}} \right ) }
\right ] *
\left [
\frac{1}{\sqrt{2\pi} \sqrt{1-\bar{a}{t-1}}} e^{\left ( -\frac{1}{2}\frac{(x{t-1}-\sqrt{\bar{a}{t-1}}x_0)^2}{1-\bar{a}{t-1}} \right ) }
\right ] \div
\left [
\frac{1}{\sqrt{2\pi} \sqrt{1-\bar{a}{t}}} e^{\left ( -\frac{1}{2}\frac{(x{t}-\sqrt{\bar{a}{t}}x_0)^2}{1-\bar{a}{t}} \right ) }
\right ] $$
$$ \frac{\sqrt{2\pi} \sqrt{1-\bar{a}{t}}}{\sqrt{2\pi} \sqrt{1-a{t}} \sqrt{2\pi} \sqrt{1-\bar{a}{t-1}} } e^{\left [ -\frac{1}{2} \left ( \frac{(x{t}-\sqrt{a_t}x_{t-1})^2}{1-a_{t}} + \frac{(x_{t-1}-\sqrt{\bar{a}{t-1}}x_0)^2}{1-\bar{a}{t-1}} - \frac{(x_{t}-\sqrt{\bar{a}{t}}x_0)^2}{1-\bar{a}{t}} \right ) \right ] } $$
$$ \frac{1}{\sqrt{2\pi} \left ( \frac{ \sqrt{1-a_t} \sqrt{1-\bar{a}{t-1}} } {\sqrt{1-\bar{a}{t}}} \right ) } exp{\left [ -\frac{1}{2} \left ( \frac{(x_{t}-\sqrt{a_t}x_{t-1})^2}{1-a_t} + \frac{(x_{t-1}-\sqrt{\bar{a}{t-1}}x_0)^2}{1-\bar{a}{t-1}} - \frac{(x_{t}-\sqrt{\bar{a}{t}}x_0)^2}{1-\bar{a}{t}} \right ) \right ] } $$
$$ \frac{1}{\sqrt{2\pi} \left ( \frac{ \sqrt{1-a_t} \sqrt{1-\bar{a}{t-1}} } {\sqrt{1-\bar{a}{t}}} \right ) } exp \left[ -\frac{1}{2} \left ( \frac{ x_{t}^2-2\sqrt{a_t}x_{t}x_{t-1}+{a_t}x_{t-1}^2 }{1-a_t} + \frac{ x_{t-1}^2-2\sqrt{\bar{a}{t-1}}x_0x{t-1}+\bar{a}{t-1}x_0^2 }{1-\bar{a}{t-1}} - \frac{(x_{t}-\sqrt{\bar{a}{t}}x_0)^2}{1-\bar{a}{t}} \right) \right] $$
$$ \frac{1}{\sqrt{2\pi} \left ( {\color{Red} \frac{ \sqrt{1-a_t} \sqrt{1-\bar{a}{t-1}} } {\sqrt{1-\bar{a}{t}}}} \right ) }
exp \left[
-\frac{1}{2}
\frac{
\left(
x_{t-1} - \left(
{\color{Purple} \frac{\sqrt{a_t}(1-\bar{a}{t-1})}{1-\bar{a}t}x_t
+
\frac{\sqrt{\bar{a}{t-1}}(1-a_t)}{1-\bar{a}t}x_0}
\right)
\right) ^2
} { \left( {\color{Red} \frac{ \sqrt{1-a_t} \sqrt{1-\bar{a}{t-1}} } {\sqrt{1-\bar{a}{t}}}} \right)^2 }
\right] $$
$$ p(x_{t-1}|x_{t}) \sim N\left( {\color{Purple} \frac{\sqrt{a_t}(1-\bar{a}{t-1})}{1-\bar{a}t}x_t + \frac{\sqrt{\bar{a}{t-1}}(1-a_t)}{1-\bar{a}t}x_0} , \left( {\color{Red} \frac{ \sqrt{1-a_t} \sqrt{1-\bar{a}{t-1}} } {\sqrt{1-\bar{a}{t}}}} \right)^2 \right) $$
Because
$$ p(x_{t-1}|x_{t}) \sim N\left( {\color{Purple} \frac{\sqrt{a_t}(1-\bar{a}_{t-1})}{1-\bar{a}t}x_t + \frac{\sqrt{\bar{a}{t-1}}(1-a_t)}{1-\bar{a}t}\times \frac{x_t - \sqrt{1-\bar{a}t}\times ϵ}{\sqrt{\bar{a}t}} } , {\color{Red} \frac{ \beta{t} (1-\bar{a}{t-1}) } { 1-\bar{a}{t}}} \right) $$