I made use of Vince Buffalo's msr and added my own function to estimate Weir & Cockerham’s Fst. This is a work-in-progress to estimate Fst between 2 population comparisons from ms and compare it to an observed distribution.
This can be done through Vince's ms() option (see below) or through stand-alone. Here, I've run the example below. This begins with 1 population that splits into 3 independant populations in 2 generations (2 pops with 100 and 1 with 635). The split is maintained for 3 generations. It outputs 2000 regions that are 100000 bp for 84 diploid samples and assumes a recombination rate of r = 22cm/Mb.
#./ms 84 2000 -t .254 -I 3 24 32 28 -n 2 0.16 -n 3 0.16 -ej 0.0012 2 1 -ej 0.0012 3 1 -r 56 100000 > testout100r2pops
setwd('/Users/brcok/Desktop/git/msrFST')
document()
## Updating msr documentation
## Loading msr
setwd('/Users/brcok/Desktop/git/')
install('msrFST')
## Installing msr
## '/Library/Frameworks/R.framework/Resources/bin/R' --no-site-file \
## --no-environ --no-save --no-restore --quiet CMD INSTALL \
## '/Users/brcok/Desktop/git/msrFST' \
## --library='/Library/Frameworks/R.framework/Versions/3.4/Resources/library' \
## --install-tests
##
## Reloading installed msr
library('msrFST')
##
## Attaching package: 'msrFST'
## The following object is masked from 'package:msr':
##
## fst
setwd('~/Desktop/git/msrFST/')
getwd()
## [1] "/Users/brcok/Desktop/git/msrFST"
x <- readLines('testout100r2pops')
y <- parse_ms(x)
inp = (y[which(y$segsites > 1),])
head(inp)
## # A tibble: 6 x 4
## rep segsites positions gametes
## <int> <dbl> <list> <list>
## 1 1 2.00 <dbl [2]> <int [84 × 2]>
## 2 5 2.00 <dbl [2]> <int [84 × 2]>
## 3 6 2.00 <dbl [2]> <int [84 × 2]>
## 4 8 2.00 <dbl [2]> <int [84 × 2]>
## 5 9 2.00 <dbl [2]> <int [84 × 2]>
## 6 10 2.00 <dbl [2]> <int [84 × 2]>
x <- (inp$gametes[1])
fst.lis <- map_dbl(inp$gametes, fst)
head(fst.lis)
## [1] 0.007456543 -0.003292748 0.043808420 0.006222053 -0.009247082
## [6] 0.077511180
#this is FST between 2 populatuions and the founding population
#load a data set of real data - here 3 pops Fst between 2 small and 1 large mai
fst.all <- read.table('pop1_vs_pop2_100000.windowed.weir.fst',header=T,colClasses = c('character', 'numeric', 'numeric', 'numeric', 'numeric', 'numeric'))
#clean the data a bit
fst.obs <- fst.all$MEAN_FST[fst.all$N_VARIANTS > 1]
fst.obs[fst.obs < 0 ] = 0
fst.lis[fst.lis < 0 ] = 0
fst.lis <- fst.lis[fst.lis>0]
fst.obs <- fst.obs[fst.lis>0]
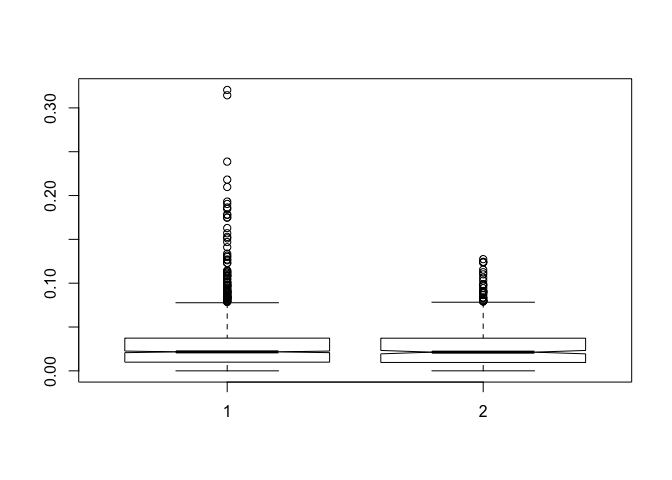
#plot it
boxplot(fst.obs, fst.lis, notch=T)
#summarize the simulated
summary(fst.lis)
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 2.225e-05 9.586e-03 2.133e-02 2.818e-02 3.689e-02 1.274e-01
#summarize the observed
summary(fst.obs)
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.000000 0.009924 0.021654 0.027189 0.037319 0.320456