/opo-evolutionary-algorithm

Apply the DEAP Framework to demonstrate the One-plus-One algorithm

Primary LanguagePython

An Evolutionary Algorithm to solve a simple function maximization problem

Sample Function:

[ f(x) = -x * 8 * x * (x - 3) * (x - 4) ]

Study:

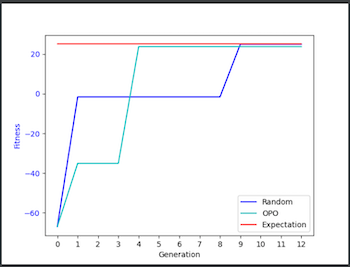
Using the DEAP Framework to demonstrate the performance of One-plus-One algorithm and compare it with the baseline Random algorithm.

One-plus-One Algorithm

  1. Set the population size being equal to 1.
  2. Evaluate the population.
  3. Mutate the best individual.
  4. Evaluate the mutants.
  5. Compare the mutation with the best and select the individual with the highest fitness value.
  6. Repeat until reaching an exception.

Random Algorithm

  1. Set the population size being equal to 1.
  2. Evaluate the population.
  3. Generate a random individual as offspring from an original individual.
  4. Compare the offspring with the best and select the individual with the highest fitness value.
  5. Store the individual with the best fitness value

Visualization Result

An Evolutionary Algorithm

Result

Execute the experiment in 12 epochs and see how the algorithm evolved.

One-plus-One Algorithm

   	     	                fitness                 	                    size                   
   	     	----------------------------------------	-------------------------------------------
gen	evals	min     	avg     	max     	avg	evals	gen	max	min	std
0  	0    	-66.8118	-66.8118	-66.8118	1  	0    	0  	1  	1  	0  
1  	1    	-1.59792	-1.59792	-1.59792	1  	1    	1  	1  	1  	0  
2  	2    	-1.59792	-1.59792	-1.59792	1  	2    	2  	1  	1  	0  
3  	3    	-1.59792	-1.59792	-1.59792	1  	3    	3  	1  	1  	0  
4  	4    	-1.59792	-1.59792	-1.59792	1  	4    	4  	1  	1  	0  
5  	5    	-1.59792	-1.59792	-1.59792	1  	5    	5  	1  	1  	0  
6  	6    	-1.59792	-1.59792	-1.59792	1  	6    	6  	1  	1  	0  
7  	7    	-1.59792	-1.59792	-1.59792	1  	7    	7  	1  	1  	0  
8  	8    	-1.59792	-1.59792	-1.59792	1  	8    	8  	1  	1  	0  
9  	9    	24.922  	24.922  	24.922  	1  	9    	9  	1  	1  	0  
10 	10   	24.922  	24.922  	24.922  	1  	10   	10 	1  	1  	0  
11 	11   	24.922  	24.922  	24.922  	1  	11   	11 	1  	1  	0  
12 	12   	24.922  	24.922  	24.922  	1  	12   	12 	1  	1  	0

Random Algorithm

   	     	                fitness                 	                    size                   
   	     	----------------------------------------	-------------------------------------------
gen	evals	min     	avg     	max     	avg	evals	gen	max	min	std
0  	0    	-66.8118	-66.8118	-66.8118	1  	0    	0  	1  	1  	0  
1  	1    	-35.0343	-35.0343	-35.0343	1  	1    	1  	1  	1  	0  
2  	2    	-35.0343	-35.0343	-35.0343	1  	2    	2  	1  	1  	0  
3  	3    	-35.0343	-35.0343	-35.0343	1  	3    	3  	1  	1  	0  
4  	4    	23.7197 	23.7197 	23.7197 	1  	4    	4  	1  	1  	0  
5  	5    	23.7197 	23.7197 	23.7197 	1  	5    	5  	1  	1  	0  
6  	6    	23.7197 	23.7197 	23.7197 	1  	6    	6  	1  	1  	0  
7  	7    	23.7197 	23.7197 	23.7197 	1  	7    	7  	1  	1  	0  
8  	8    	23.7197 	23.7197 	23.7197 	1  	8    	8  	1  	1  	0  
9  	9    	23.7197 	23.7197 	23.7197 	1  	9    	9  	1  	1  	0  
10 	10   	23.7197 	23.7197 	23.7197 	1  	10   	10 	1  	1  	0  
11 	11   	23.7197 	23.7197 	23.7197 	1  	11   	11 	1  	1  	0  
12 	12   	23.7197 	23.7197 	23.7197 	1  	12   	12 	1  	1  	0

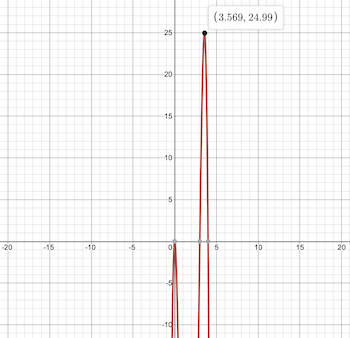
Compare the final result with the global maximum of the graph function to evaluate the algorithm performance.

An Evolutionary Algorithm

Fig. 2: The global maximum of the given function