#Projeto PDS
Hélio de Meira Lins Neto
Ferramentas
Todo o projeto foi feito usando ferramentas opensource. Seguem as ferramentas usadas:
- Python
- Pillow
- Numpy
- Scypy
- Matplotlib
- Tesseract-ocr ( pytesseract)
- Octave
##Parte 1
###Questão 1
Código: parte1/q1.py
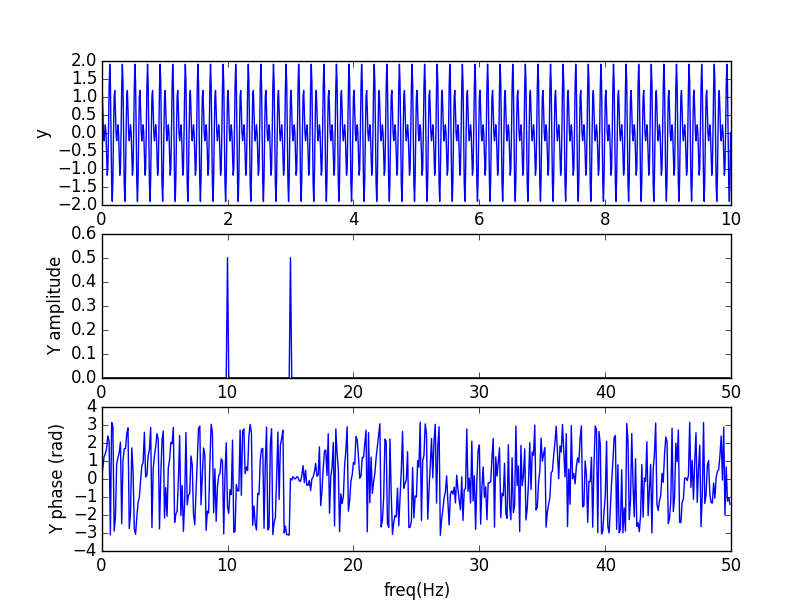
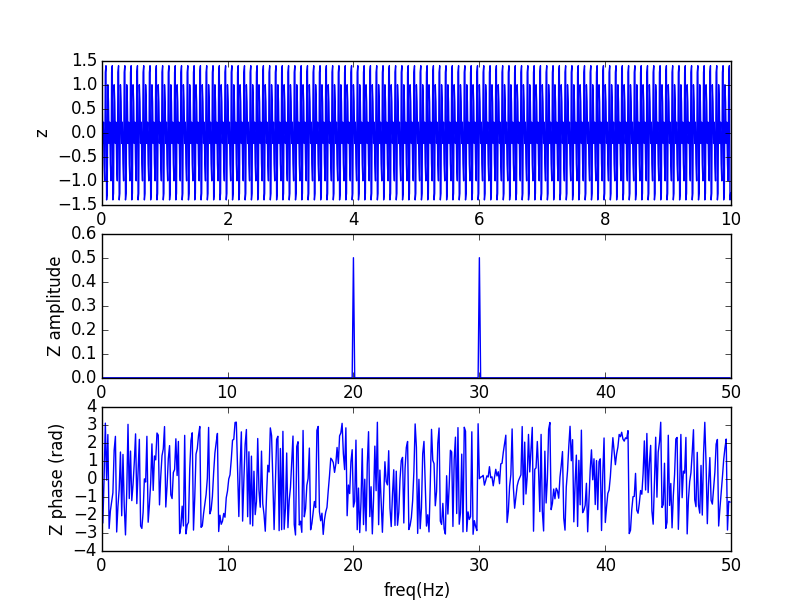
Gráficos das letras a), b) e c). Todos feitos usando Numpy/Scipy.
d)
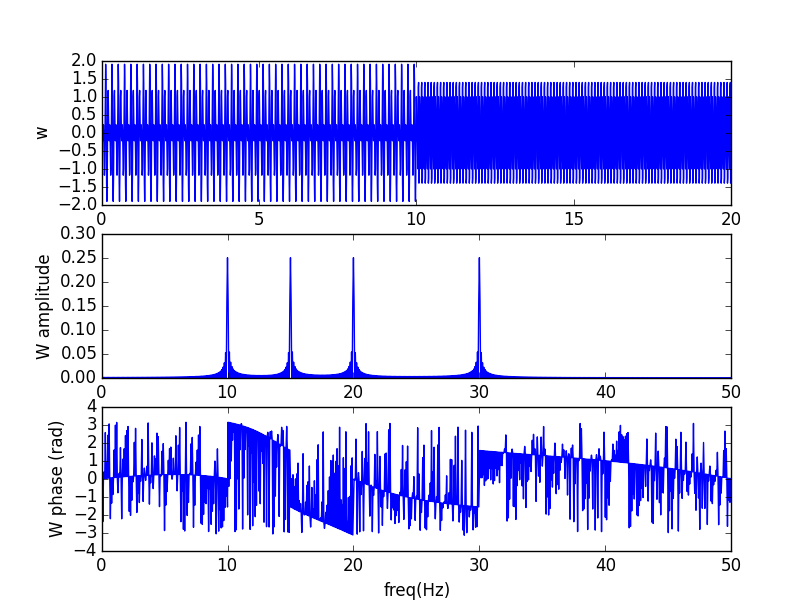
A função z tem o dobro da frequência da função y. Assim, a transformada de fourier Z(f)=Y(f/2) e seus picos são em pontos com o dobro da frequência dos de y. A transformada da função w, obtida a partir da concatenação das anteriores, possui os picos de Z e de Y. Note que, graficamente, não é possível inferir quando as frequências estão ativas.
e)
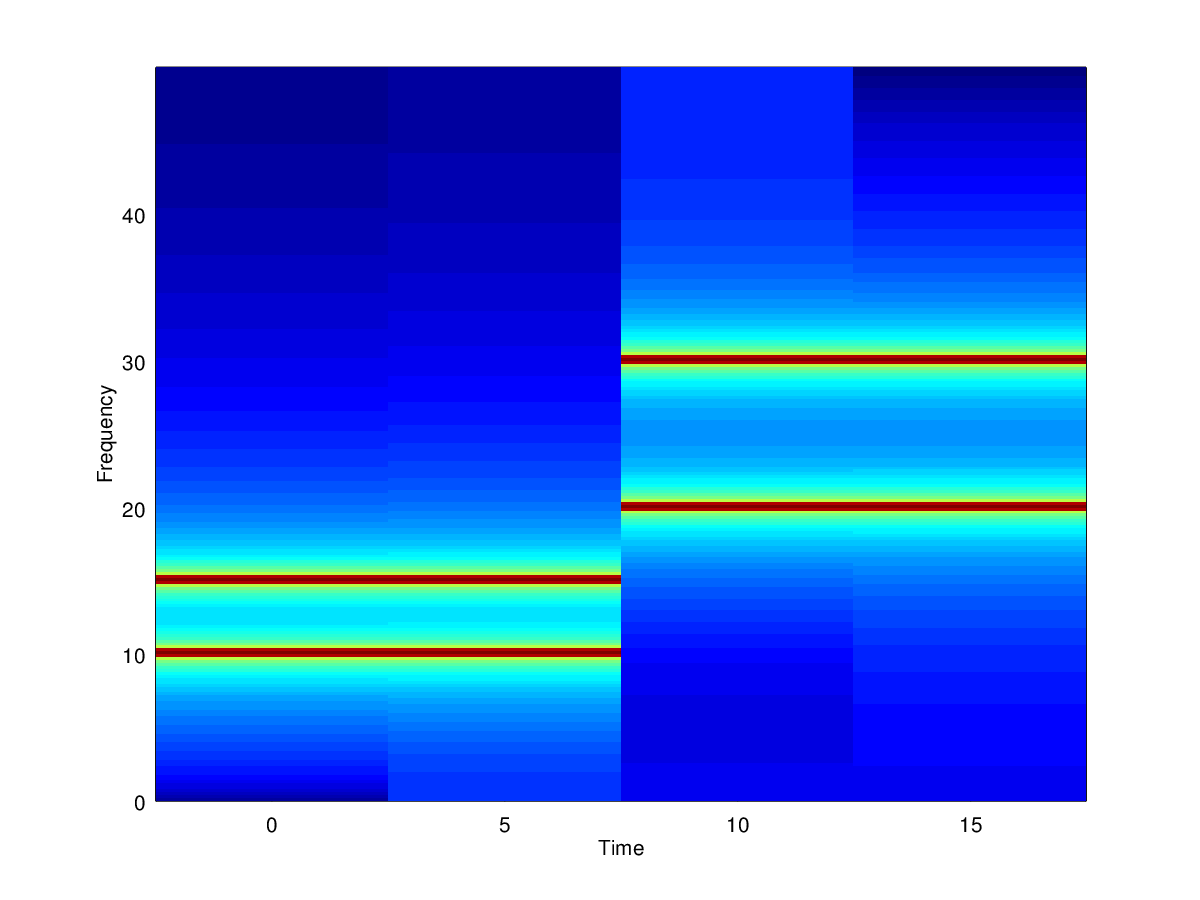
As bibliotecas Numpy e Scipy não tem uma função pronta do espectograma. Para evitar implementá-la, usei o GNU Octave. Seguem os comandos:
pkg load signal
t = [0:0.01:9.99];
w = [sin(20*pi*t) + cos(30*pi*t), sin(40*pi*t) + cos(60 * pi * t)];
specgram(w, 256, 100, 500)
Agora vemos as componentes de frequência pelo tempo, o que não era claro na transformada de fourier. Isso acontece pois o espectrograma faz transformadas de fourier em subintervalos.
Parte2
Questão 1
Código: parte2/q1.py
A maneira mais simples de resolver o problema dos Ringings é aplicando um filtro passa baixa. Apliquei um filtro gaussiano (do scipy) com sigma 1.5. Segue o resultado:
A desvantagem do filtro gaussiano é que ele embaça bastante a foto. Provavelmente, pode-se obter um resultado melhor usando filtro sinc. fonte: https://en.wikipedia.org/wiki/Ringing_artifacts#Causes
Questão 2
Código: parte2/q2.py Parte mais relevante do código:
text = pytesseract.image_to_string(img)
without_spaces = re.sub('\s+', '', text)
print(len(without_spaces))
Não obtive muito sucesso com meus algoritmos, então apelei para o Tesseract, que é uma ferramenta para reconhecer textos em imagens. Bastou apenas remover os espaços e os \n ( usei expressões regulares). Número de caracteres: 211.
Minha implementação está no arquivo parte2/alternativeq2.py. Basicamente, eu aplico uma transformação na imagem para eliminar os ruídos da imagem e separo em regiões que são mais escuras que a média da imagem. Infelizmente, algumas letras estão muito próximas e são consideradas juntas. Da mesma maneira, temos problemas com ruídos e devemos filtrar as regiões que são muito pequenas.
Obtive um resultado de 199 para regiões com tamanho maior que 5 pixels, e 197 para regiões com mais de 10. Não é muito relevante, mas regiões maiores que 2 pixels dá 211! Mesma resposta do outro algoritmo.
Obtive resultados melhores trocando a condição de ser mais escuro que a média por valores fixos, mas deixei dessa maneira para funcionar com mais imagens.
Questão 3
Analisando as componentes RGB da imagem separadamente( e em tons de cinza), notei que o número fica evidente ao comparar as imagens das componentes R e G ( passando de uma para outra, como em um slideshow). Comparar a componente azul com qualquer uma das outras duas não deixou o número evidente para mim. Assim, decidi trocar as componentes vermelhas e verdes assim:
cb[:, :, 0] = 255 / 2 + (dalton[:, :, 0] - dalton[:, :, 1])
cb[:, :, 1] = 255 / 2 + (dalton[:, :, 1] - dalton[:, :, 0])
Resulta em:
É meio difícil explicar a motivação de tal transformação, mas devo dizer que foram várias tentativas até chegar nesta, que deixa bem evidente a distinção. Também é possível obter resultados ainda melhores aumentado o fator que multiplica a diferença das componentes R e G, ou deixando o vermelho mais claro e o verde mais escuro. Exemplo:
cb[:, :, 0] = 3*255 / 4 + (dalton[:, :, 0] - dalton[:, :, 1])
cb[:, :, 1] = 255 / 4 + (dalton[:, :, 1] - dalton[:, :, 0])
Retirando a cor azul da jogada:
Parte 3
Código: parte3/parte3.py
Na parte 3, tomei a solução mais simples possível. Simplesmente:
imsave('inter_102.bmp', img101 / 2 + img103 / 2)
imsave('inter_110.bmp', img109 / 2 + img111 / 2)
imsave('inter_118.bmp', img117 / 2 + img119 / 2)
Frames:
Parte 4
Questão 1
Código: parte4/q1.py
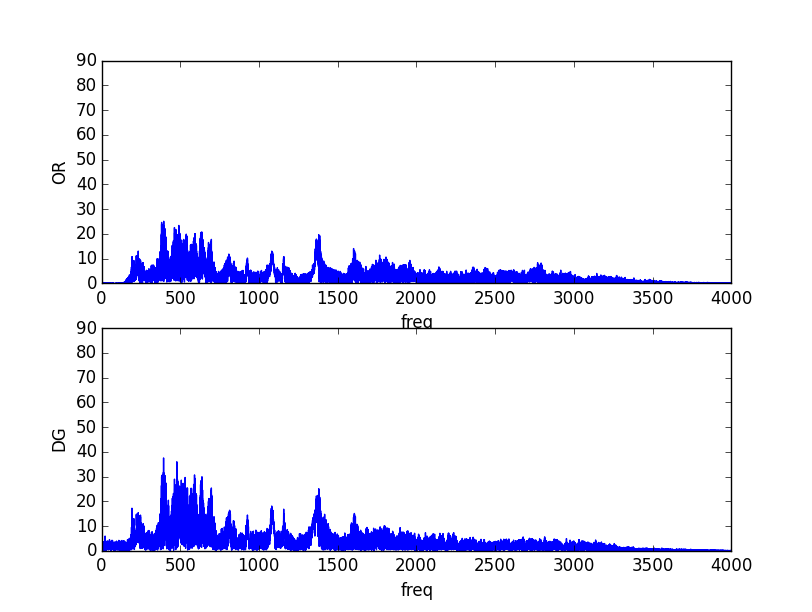
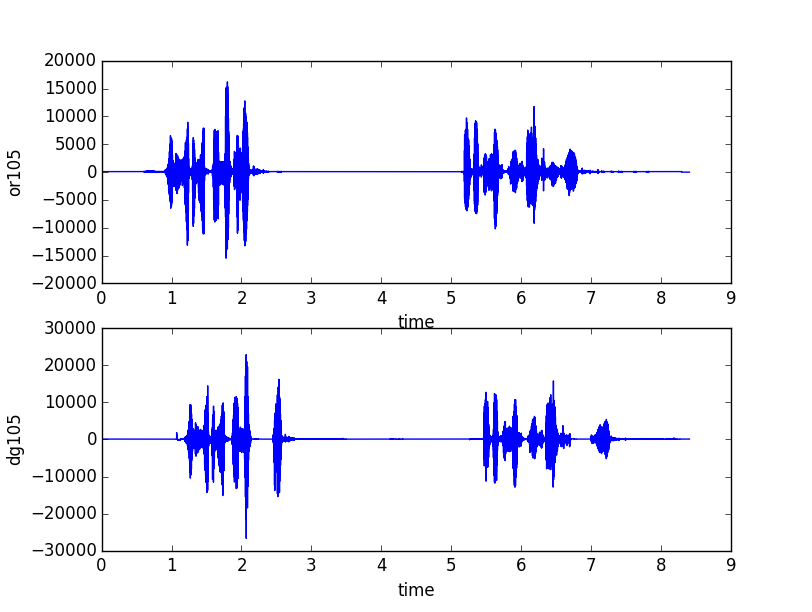
Analisamos os sinais nos domínios do tempo e da frequência:
Percebemos que há atrasos e perdas.
Questão 2
Código: parte4/q2.py
Taxa de Amostragem: 8kHz
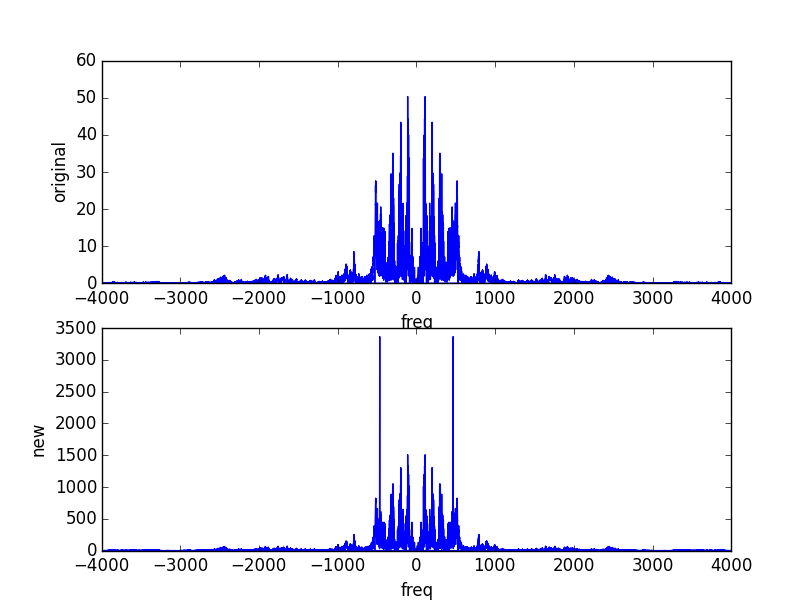
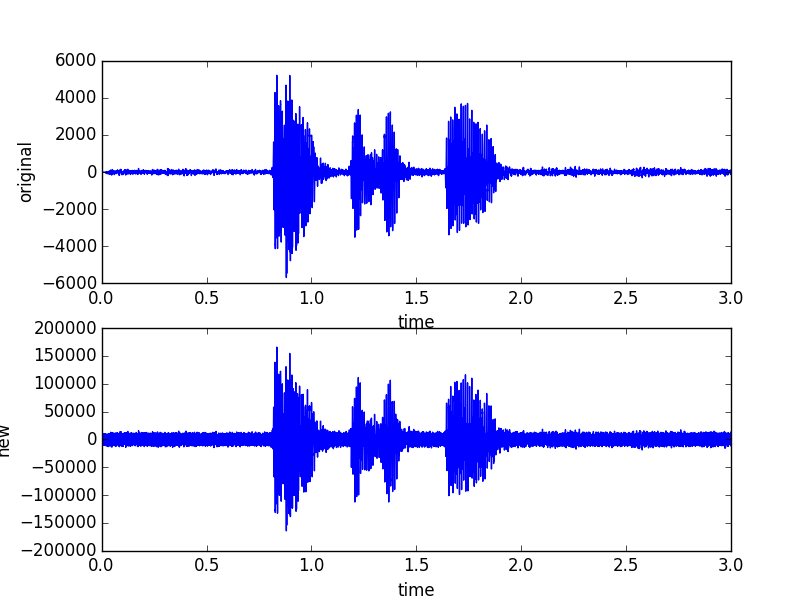
Primeiramente, removi o ruído zerando uma banda de frequência na transformada de fourier, e depois tirando a transformada inversa. Só pra checar mesmo.
Apliquei um Filtro Fir ( janela de kaiser, width=1/fs, ripple_db = 11). Os coeficientes foram divididos por 10000 para diminuir o ruído. O resultado foi bastante satisfatório. Brinquei com vários valores de filtros de Kaiser e obtive resultados satisfatórios. Não consegui obter bons resultados com filtros de Chebyshev.