The working paper describing this approach can be found here: https://arxiv.org/abs/2406.12661
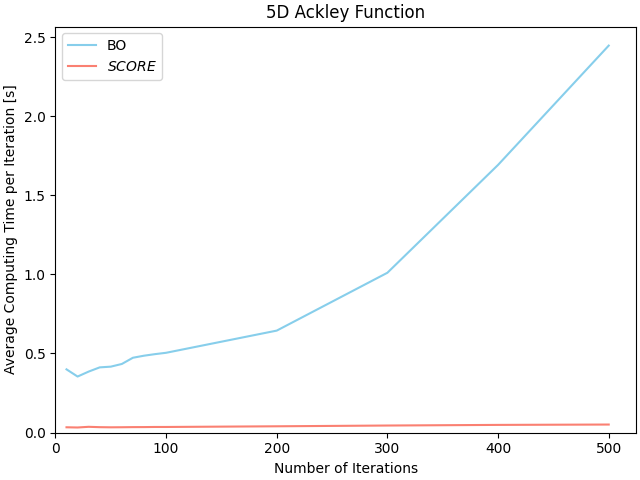
If you follow example.py (and take a closer look at SCORE.py) you'll notice that just as with standard BO, the objective function (the Ackley function in this case: https://www.sfu.ca/~ssurjano/ackley.html) is first evaluated at random n_init initial points (or init_combs pre-defined initial combinations). Then, much like deriving the marginal probability distribution of a single variable from the joint probability distribution describing the relationship between multiple variables, each parameter is considered alone while marginalizing out the others. But instead of integrating over all the possible values of the other parameters, only the minimum (or maximum) value achieved so far for the objective function is recorded. This enables fitting the surrogate model to individual (discrete or continuous) variables and significantly reduces the computational load, which becomes dependent on the number of input parameters and their mesh resolution (bounds) – rather than the number of iterations nb_it.
Next, the acquisition function (af) is computed to assign a "score" to every possible parameter value. These individual parameter scores are then aggregated to identify the most promising parameter combination for objective function testing. Instead of suggesting just one point (i.e. the parameter combination with the best score), multiple combinations can alternatively be selected at every iteration (via n_cbs). Therefore, for the same total number of function evaluations, the number of times the surrogate model is called is greatly reduced while potentially accelerating convergence toward the global optimum.
So far, only minimization problems with discrete variables are considered. While we have been successfully using
Contact Information
| Joseph Chakar | PhD student @ Ecole Polytechnique, IP Paris | joseph.chakar@polytechnique.edu |
| Pierre-Antoine Amiand-Leroy | Machine Learning Engineer @ Hi! PARIS | pierre-antoine.amiand-leroy@ip-paris.fr |