This script implements a 2d fluid solver based on Lattice Boltzmann method using Taichi programming language. The high-performance cross-platform CFD (computational fluid dynamics) solver can be achieved within 200 lines thanks to taichi.
To numerically solve a fluid-dynamics problem, the domain size, fluid property, boundary conditions and initial conditions should be given. In this code, these parameters can be specified by instancing the solver:
lbm = lbm_solver(nx, ny, niu, bc_type, bc_value)
The meaning of each parameter is:
nx,nydefine domain size. Note that they are given in dimensionless form (ie. lattice units), which assumesdx = dy = dt = 1.0, wheredxanddyare discrete grid sizes,dtis the time interval of one step.niuis the fluid viscosity in lattice units. Note there is a transformation between SI units and lattice units.bc_typeis a four-element python list denoting the[left, top, right, bottom]boundary condition type. The velocity at the boundary is set based onbc_type. Ifbc_type = 0, velocity is set as constant value (Dirichlet condition ) given inbc_value. Ifbc_type = 1, the derivative of velocity in boundary normal direction is set to zero (Neumann condition).bc_valueis a(4,2)python list, it gives constant velocity value at each boundary whenbc_type = 0.
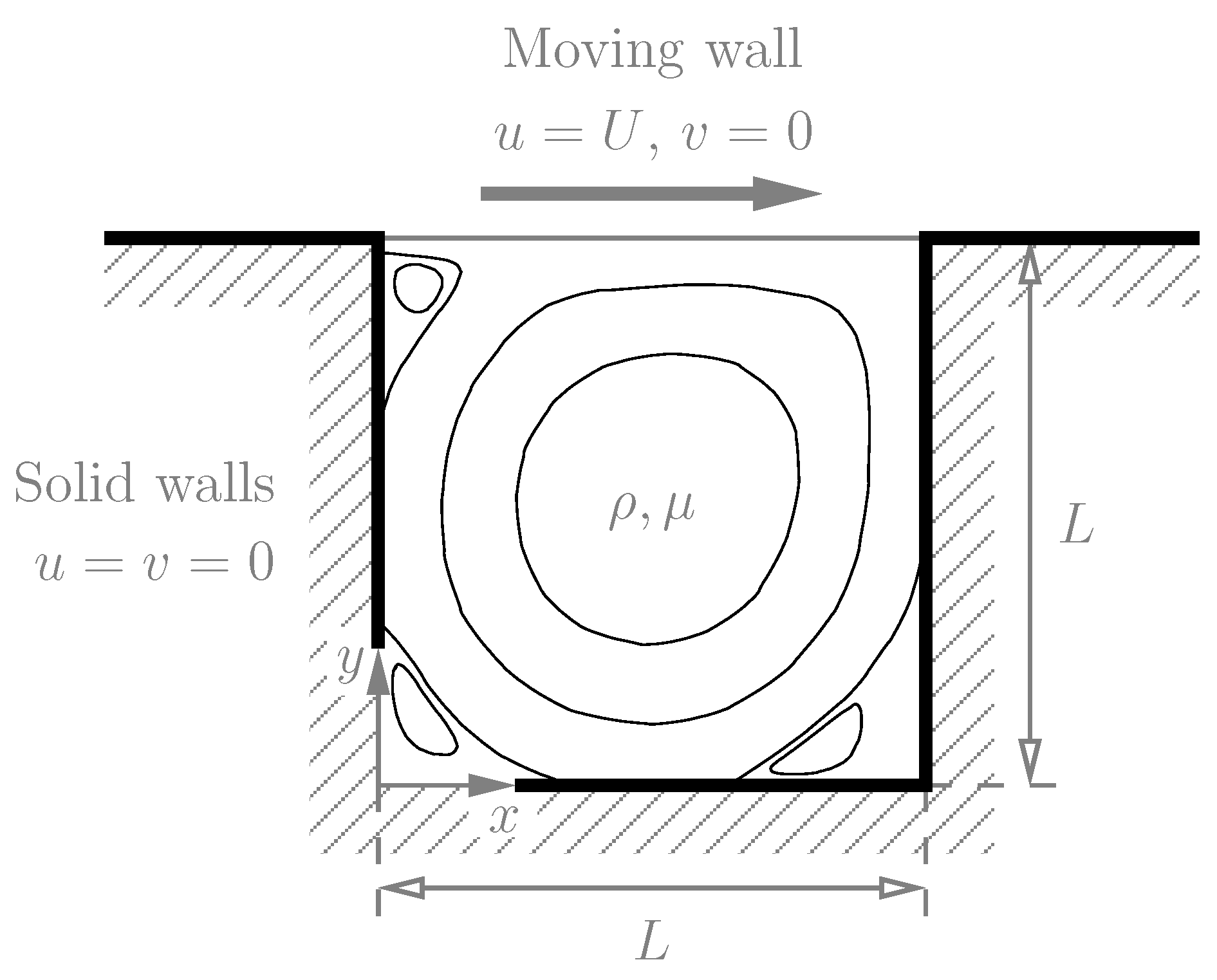
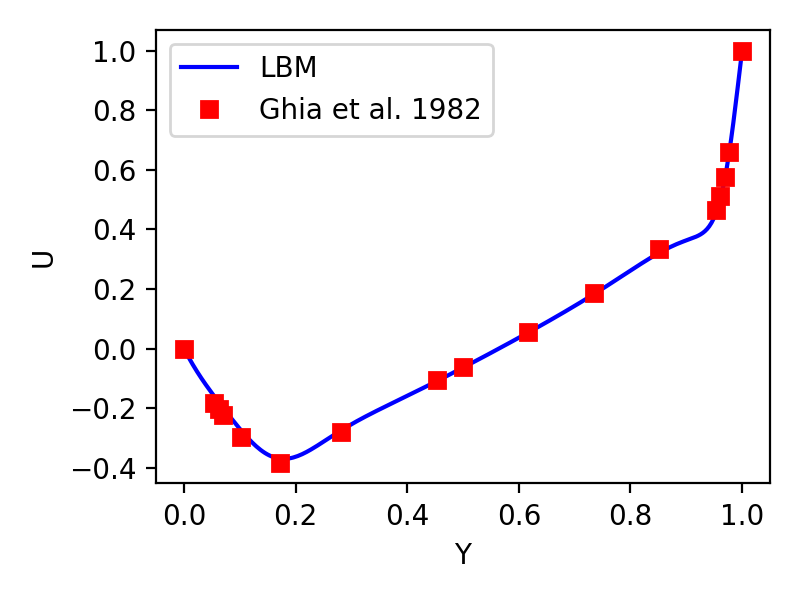
Lid-driven cavity flow is benchmark fluid-dynamics problem used to verify the solver accuracy. To compare simulation results based on different unit-systems, the flow Reynolds number Re should keep the same. In this case, Re is defined as Re = U * L / niu, so a solver with Re = 1000 can be given by:
lbm = lbm_solver(256, 256, 0.0255, [0, 0, 0, 0],
[[0.0, 0.0], [0.1, 0.0], [0.0, 0.0], [0.0, 0.0]])
Here Re = U * (nx-1) * dx / niu = 0.1 * 255.0 / 0.0255. The velocity magnitude is shown in the contour below and x-component of velocity in the middle line is compared with result from literature.
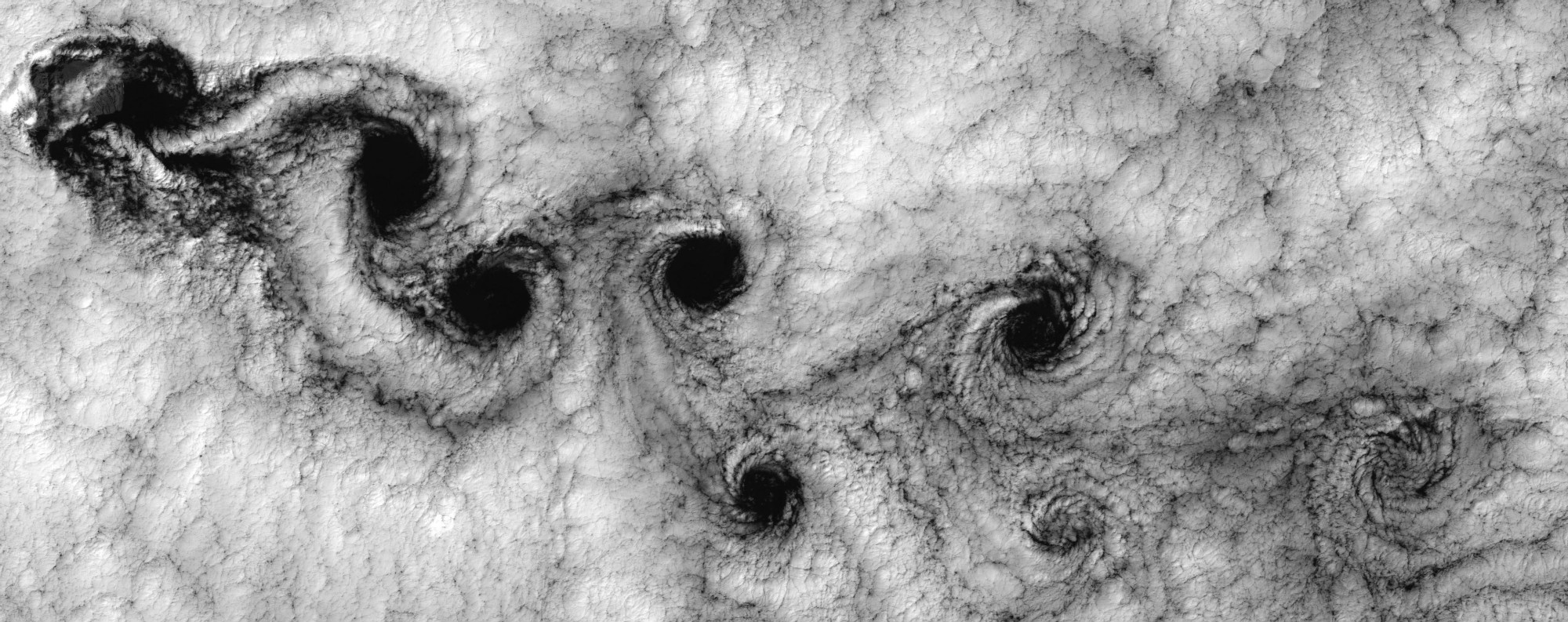
Kármán vortex street is an interesting phenomenon in fluid dynamics. When fluids flow pass blunt body (say a cylinder), there exists a repeating pattern of swirling vortices, caused by a process known as vortex shedding. The Reynolds number of this flow is defined as Re = U * D / niu, where D means diameter. A solver with Re = 200 can be given by:
lbm = lbm_solver(401, 101, 0.005, [0, 0, 1, 0],
[[0.1, 0.0], [0.0, 0.0], [0.0, 0.0], [0.0, 0.0]],
1, [80.0, 50.0, 10.0])