Dynamic programming is a strategy for developing an algorithm where each subproblem is solved and the results recorded for use in solving larger problems. In this exercise you will write a pair of dynamic programming methods.
[Newman-Conway sequence] is the one which generates the following integer sequence. 1 1 2 2 3 4 4 4 5 6 7 7….. and follows below recursive formula.
P(1) = 1
P(2) = 1
for all n > 2
P(n) = P(P(n - 1)) + P(n - P(n - 1))
Given a number n then print n terms of Newman-Conway Sequence
Examples:
Input : 13
Output : 1 1 2 2 3 4 4 4 5 6 7 7 8
Input : 20
Output : 1 1 2 2 3 4 4 4 5 6 7 7 8 8 8 8 9 10 11 12
You should be able to do this in O(n) time complexity.
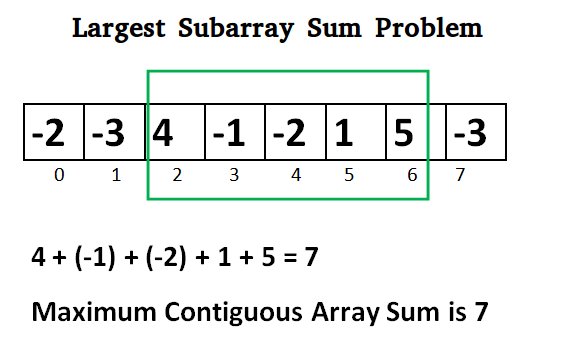
Write a method to find the contiguous subarray in a 1-dimensional array with the largest sum.
This can be solved using Kadane's Algorithm
Initialize:
max_so_far = 0
max_ending_here = 0
Loop for each element of the array
(a) max_ending_here = max_ending_here + a[i]
(b) if(max_ending_here < 0)
max_ending_here = 0
(c) if(max_so_far < max_ending_here)
max_so_far = max_ending_here
return max_so_far
The idea of the Kadane’s algorithm is to look for all positive contiguous segments of the array (max_ending_here is used for this). And keep track of the maximum sum contiguous segment among all positive segments (max_so_far is used for this). Each time we get a positive sum compare it with max_so_far and update max_so_far if it is greater than max_so_far
There is also a subtle divide & conquer algorithm for this.