A fairly basic script to search over a range of lambda values for Elastic Weight Consolidation. Different sequential tasks can be configured for testing, as well as different search parameters and base models. An overview of this program is below.
This project is a spin off of a much larger research project undertaken at the University of Otago. This project was small part of the larger whole, but is interesting and independent enough to be preserved alone.
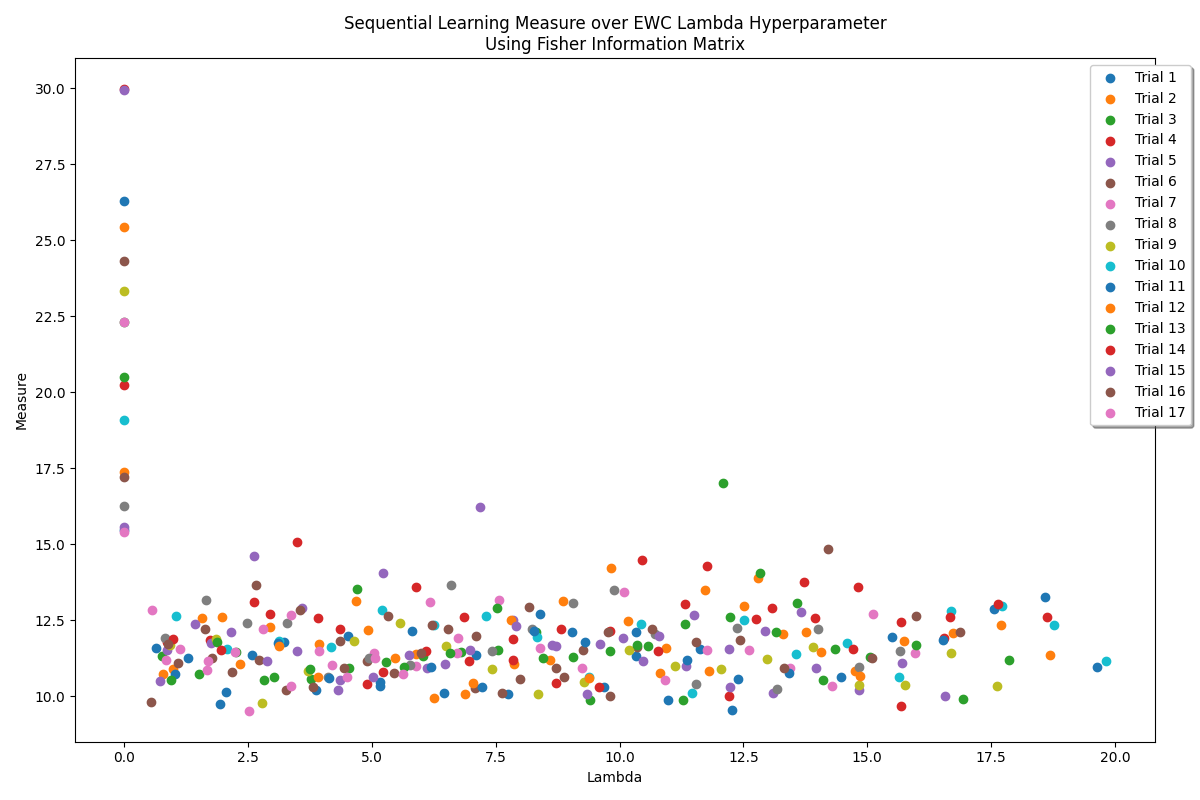
Above is a graph detailing many trials of sequential learning on the MNIST dataset. In the above, each trial is an attempt for a network to first classify digits 0,1,2 and then subsequently classify digits 3,4,5. To measure the performance of EWC in each trial we integrated (using a Riemann sum) over the loss of each task after it had been introduced. Therefore a good trial will have a low loss on all tasks once introduced, and will have a lower measure. In the graph above, we should see a clear minimum of the measure at some value of lambda - but instead we find a noisy region with no clear minimum. This shows that the stochastic nature of training is overwhelming the ability to measure EWC performance - each trial is (and each lambda test within each trial) is different enough to mask the EWC effect on the measure! At best we may be able to determine which weight importance measures are best from this data.
See the below sections for a more detailed explanation of what this project attempts.
Sequential Learning is a problem in AI research that focuses on how artificial neural networks train on several tasks in sequence. Traditionally, neural networks are trained on all available data simultaneously, allowing for the maximal performance across that data. It is not difficult to engineer a scenario in which data is not available all at once. Instead of training on all data at once, what if we trained a model on some first subset, then on a second set without using the first set again? This is the core of sequential learning.
Unfortunately, sequential learning usually leads to catastrophic forgetting - the model tends to entirely forget the first set of data after learning the second. This is not seen in biological neural networks. Catastrophic forgetting would be like a human learning to drive and forgetting how to walk!
Many approaches have been taken to mitigate catastrophic forgetting. In this project we are focusing on a single method: Elastic Weight Consolidation. In EWC we train a model on a task (a set of data) then record the position on the model in weight space. Then, while training on the next task, we add a term to the loss function that penalizes movement in the weight space. Importantly, we do not have to penalize all weight movements uniformly - we could effectively freeze some weights and leave others completely free! This allows the model to remember the first task after training on the second task by greatly penalize weights important to the first task.
One problem with EWC is the introduction of a new hyperparameter lambda. Lambda controls how much we add the new penalty term in comparison to the traditional loss function. A larger lambda will recall the first task better at the expense of possibly learning the second task worse.
This project looks at finding optimal values of lambda for different tasks, weight importance measures, and models.
First, select the sequential task to train on. A selection of tasks are presented under the SequentialLearning/Tasks directory. For example, the MNISTClassificatioTask would have models classify digits (10 classes). Ensure to change the import to the task you require (line 22).
With a task selected, configure the initial parameters of the training. A summary of parameters are given below. Unfortunately, parameters can currently only be set by editing the file directly. I have not put in the time to make these parameters into command line arguments or config files. Sorry! Issue a pull request if you want!
With task and parameters ready, you can set the base model under the create_and_save_base_model function. Some tasks will require larger or smaller models, or different architectures. Once you are happy with your model structure, it is time to run the program!
This program loops forever, attempting new trials looking for optimal values of lambda. Each trial consists of finding lower/upper initial bounds on lambda (see parameter summary below), creating a base model to be used for all steps in the trial (for consistency), and finding all values of lambda to be searched during this pass (determined by the num_steps parameter). Then, for each step (value of lambda), the program trains the model on the tasks. Each value of lambda has its performance in sequential learning measured (see the measure_lambda_performance function) and recorded. Finally, after all steps are complete, the optimal value of lambda is selected as the new midpoint of a reduced search range, and the process is repeated until the search range is sufficiently small.
To exit the program, press CTRL+C to quit. Data and models are saved after each step.
task_classes: A list of lists indicating what classes should be introduced in each sequential task.epochs: The number of epochs to train each task for.batch_size: The size of each batch during training. If encountering out-of-memory errors, try lowering the batch size!ewc_method: An enum to select the weight importance measure. Several are given under theSequentialLearning/EWC_Methodsdirectory. These can be confusing at first - further reading may help understanding. Otherwise, the fisher matrix tends to perform best.SEARCH_LOW_PARAM_RANGE: A tuple representing the range of possible lower bounds on the lambda search. Note at the start of each trial a random lower bound is selected from this range, for randomness. Good values of lambda are almost certainly between 0-100 (probably 0-10).SEARCH_HIGH_PARAM_RANGE: A tuple representing the range of possible upper bounds on the lambda search. Note at the start of each trial a random upper bound is selected from this range, for randomness. Good values of lambda are almost certainly between 0-100 (probably 0-10).NUM_STEPS: The number of steps to take from the lower parameter to the upper parameter. A larger number of steps will take much longer but provide fine-grained data.SEARCH_TERMINATION_THRESHOLD: Value to indicate end of a trial. When all steps have been tested, the program finds the optimal value of lambda from all steps, then sets the lower and upper bounds on lambda to the steps before and after the optimal value, respectively. This allows for a sort of recursive search that can hone in on the optimal value. Once the search range is small enough (high-low <SEARCH_TERMINATION_THRESHOLD) then the trial is over and a new trial can begin.