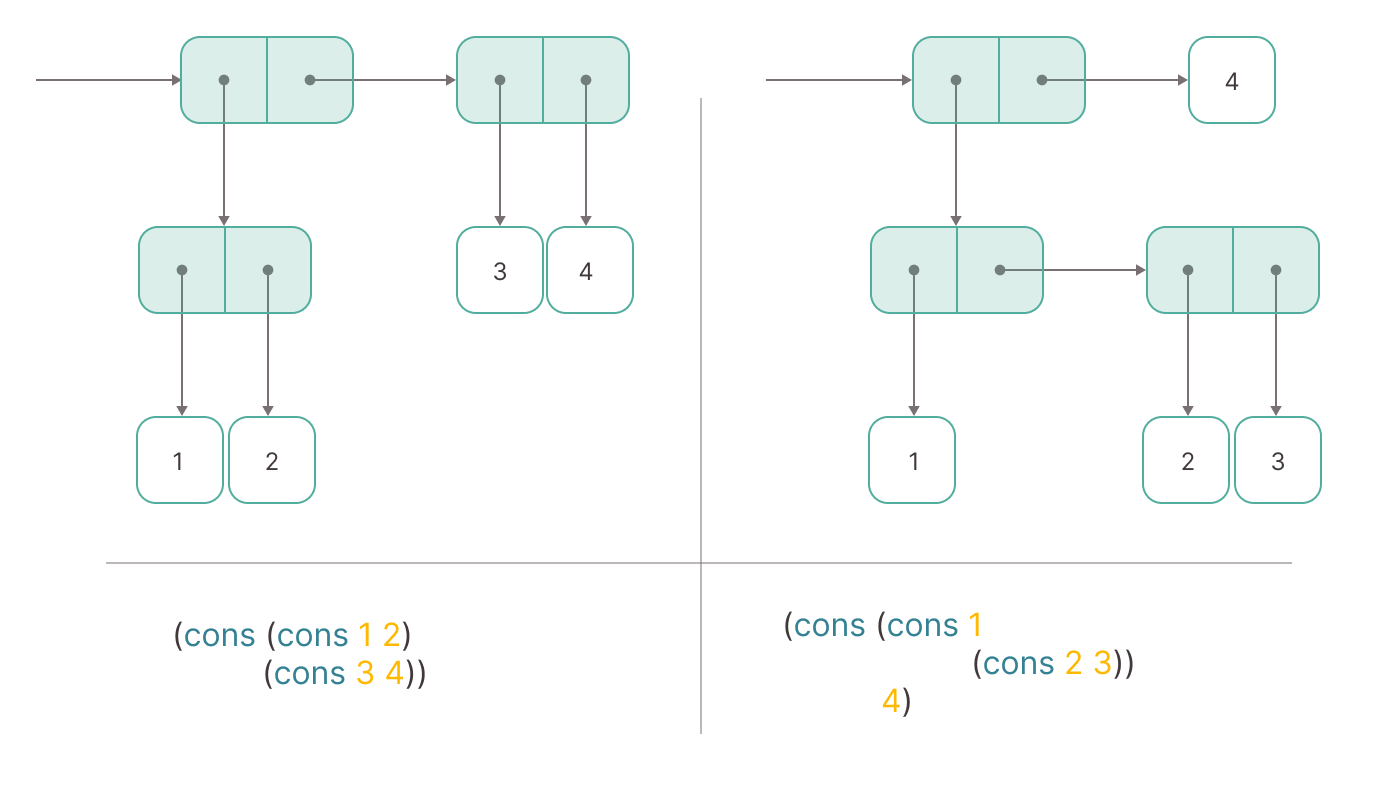
Constructor of TypeScript symbolic expressions.
<1kB | no deps | tree-shakeable | side-effect free
import { car, cdr, cons } from 'ts-expression';
import type { Cons } from 'ts-expression/cons';
type X = number;
type Y = number;
type Point = Cons<X, Y>;
const makePoint = (x: X, y: Y): Point => cons(x, y);
const getX = (point: Point) => car(point);
const getY = (point: Point) => cdr(point);
const getSymmetricalPoint = (point: Point) => {
const x = getX(point);
const y = getY(point);
return makePoint(-x, -y);
};
const calculateDistance = (point1: Point, point2: Point) => {
const [x1, y1] = [getX(point1), getY(point1)];
const [x2, y2] = [getX(point2), getY(point2)];
return Math.sqrt((x2 - x1) ** 2 + (y2 - y1) ** 2);
};
//
const point1 = makePoint(3, 4);
const point2 = makePoint(0, 0);
getX(point1); // 3
getY(point2); // 0
getSymmetricalPoint(makePoint(1, 5)); // makePoint(-1, -5)
calculateDistance(makePoint(-2, -3), makePoint(-4, 4)); // ≈ 7.28TS-Expression stands for TypeScript (TS) + symbolic expression (s-expression). It is a lightweight TypeScript library inspired by LISP's cons/car/cdr operations for S-expressions. It brings functional programming concepts to TypeScript, enabling immutable data structures and encouraging robust, predictable code. This minimalist approach to handling complex data structures is particularly useful for algorithmic tasks and data manipulation, allowing developers to leverage powerful functional programming techniques in a familiar JavaScript/TypeScript environment.
Via npm
npm install ts-expressionVia yarn
yarn add ts-expressionVia pnpm
pnpm add ts-expressionVia bun
bun add ts-expressionConstructs a cons symbolic expression from two values, car and cdr.
This function creates a symbolic expression that allows access to its car (first/left element) and cdr (second/right element)
using specific messages. The resulting s-expression is an immutable structure where car and cdr can be
accessed via the messages CAR and CDR, respectively.
carCAR The first/left element of the s-expression.cdrCDR The second/right element of the s-expression.
// Creating a symbolic expression with a number and a string
const sexp = cons(5, 'hello');
// Accessing the first element using `CAR`
const five = sexp(CAR); // 5
// Accessing the second element using `CDR`
const hello = sexp(CDR); // 'hello'- Throws Error Throws an error if an unknown message is provided to the
conss-expression.
Returns Cons<CAR, CDR> A cons s-expression, which is a function that returns the car or cdr
based on the provided message.
Retrieves the first element of a cons symbolic expression (known as car).
This function returns the left element of a symbolic expression created by the cons function. It ensures that
the provided argument is a valid cons symbolic expression before attempting to access the element.
consCons<CAR, CDR> Theconssymbolic expression from which to retrieve the first element.
// Example usage
const sexp = cons(5, 'hello');
// Retrieves the first element of the symbolic expression
const five = car(sexp); // 5- Throws ReferenceError Throws an error if the provided argument is not a valid
conssymbolic expression.
Returns CAR The first element (car) of the cons symbolic expression.
Retrieves the second element of a cons symbolic expression (known as cdr).
This function returns the right element of a symbolic expression created by the cons function. It ensures that
the provided argument is a valid cons symbolic expression before attempting to access the element.
consCons<CAR, CDR> Theconssymbolic expression from which to retrieve the second element.
// Example usage
const sexp = cons(5, 'hello');
// Retrieves the second element of the symbolic expression
const hello = cdr(sexp); // 'hello'- Throws ReferenceError Throws an error if the provided argument is not a valid
conssymbolic expression.
Returns CDR The second element (cdr) of the cons symbolic expression.
Converts a cons symbolic expression into its string representation, handling nested cons s-expression recursively.
This function generates a string representation of a cons s-expression by retrieving its car and cdr
elements, converting them to strings using JSON.stringify, and formatting them in a tuple-like format.
If either car or cdr is a nested cons s-expression, the function will recursively convert those elements
to strings as well.
consCons<CAR, CDR> Theconss-expression to be converted to a string.
// Example usage
const sexp = cons(cons(1, 2), cons('hello', 'world'));
// Convert the nested symbolic expression to a string
const str = toString(sexp); // "((1, 2), ("hello", "world"))"- Throws ReferenceError Throws an error if the provided argument is not a valid
conss-expression.
Returns string A string representation of the cons s-expression, including nested s-expressions, in the format (head, tail).
Checks if the provided argument is a cons symbolic expression.
This function determines if the given value is a cons s-expression by checking if it is a function and has
a specific init property set to true. This property is used as a marker to identify cons s-expression,
which are functions with the init property indicating their construction.
maybeConsany The value to be checked. It can be of any type.
// Example of a valid cons
const sexp = cons(5, 'hello');
// Checking if it's a cons
const isValid = isCons(sexp); // true
// Example of an invalid cons
const notSexp = { car: 5, cdr: 'hello' };
// Checking if it's a cons
const isInvalid = isCons(notSexp); // falseReturns boolean true if the argument is a cons symbolic expression; otherwise, false.
Asserts that the provided argument is a valid cons s-expression and throws a ReferenceError if it is not.
This function checks whether the given argument is a valid cons s-expression using the isCons function.
If the argument is not a valid s-expression, an error is thrown with a detailed message that includes
the serialized form of the invalid argument.
maybeConsany The value to be checked, which can be of any type.
// Example of a valid cons
const sexp = cons(5, 'hello');
// Asserting the cons, no error is thrown
assertCons(sexp);
// Example of an invalid cons
const notSexp = { car: 5, cdr: 'hello' };
// Asserting the non-s-expression, an error is thrown
assertCons(notSexp); // Throws ReferenceError: Argument must be a symbolic expression, but it was '{"car":5,"cdr":"hello"}'- Throws ReferenceError Throws an error if the provided argument is not a valid
conss-expression.
Returns void
Rational numbers as pairs of values: numerator and denominator.
import type { Cons } from 'ts-expression/cons';
import { car, cdr, cons } from 'ts-expression';
import { toString } from 'ts-expression/operators';
type Numerator = number;
type Denominator = number;
type Fraction = Cons<Numerator, Denominator>;
const make = (numer: Numerator, denom: Denominator) => cons(numer, denom);
const numer = (rat: Fraction): Numerator => car(rat);
const denom = (rat: Fraction): Denominator => cdr(rat);
const isEqual = (rat1: Fraction, rat2: Fraction): boolean =>
numer(rat1) * denom(rat2) === denom(rat1) * numer(rat2);
const add = (rat1: Fraction, rat2: Fraction): Fraction => {
const [a, b] = [numer(rat1), denom(rat1)];
const [c, d] = [numer(rat2), denom(rat2)];
return make(a * d + b * c, b * d); // (a * d + b * c) / (b * d)
};
const sub = (rat1: Fraction, rat2: Fraction): Fraction => {
const [a, b] = [numer(rat1), denom(rat1)];
const [c, d] = [numer(rat2), denom(rat2)];
return make(a * d - b * c, b * d); // (a * d - b * c) / (b * d)
};
const mul = (rat1: Fraction, rat2: Fraction): Fraction => {
const [a, b] = [numer(rat1), denom(rat1)];
const [c, d] = [numer(rat2), denom(rat2)];
return make(a * c, b * d); // (a * c) / (b * d)
};
const div = (rat1: Fraction, rat2: Fraction): Fraction => {
const [a, b] = [numer(rat1), denom(rat1)];
const [c, d] = [numer(rat2), denom(rat2)];
return make(a * d, b * c); // (a * d) / (b * c)
};
//
const rat1 = make(2, 3);
const rat2 = make(4, 6);
const rat3 = make(7, 2);
toString(rat2); // '(4, 6)'
isEqual(rat1, rat2); // true
add(rat1, rat3); // 25/6
sub(rat3, rat1); // 17/6
mul(rat1, rat3); // 14/6
div(rat1, rat3); // 4/21I’ve embraced the "Structure and Interpretation of Computer Programs" (SICP) and LISP's abstractions to deeply understand and appreciate functional programming and data manipulation. These foundational concepts highlight the power of simple, immutable data structures in building complex systems, emphasizing clarity and expressive power in code.