This is a PyTorch implementation of https://arxiv.org/pdf/1503.03585.pdf
pip install git+https://github.com/hrbigelow/diffusion.git
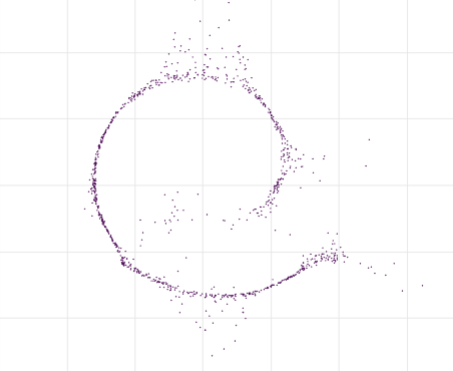
Learning the Swiss Roll distribution using diffusion trained with no mathematical analytic simplifications.
Pip requirements: fire, bokeh, torch
This is an implementation of the swiss roll model from Sohl-Dickstein et al. (2015) described in Appendix D.1.1.
Unlike in the paper, this model is trained using a brute-force Monte-Carlo sampling
procedure to minimize
One example of the learned drift term, displayed here as a vector field. The
line lengths are actual size - that is, the gridded start points represent
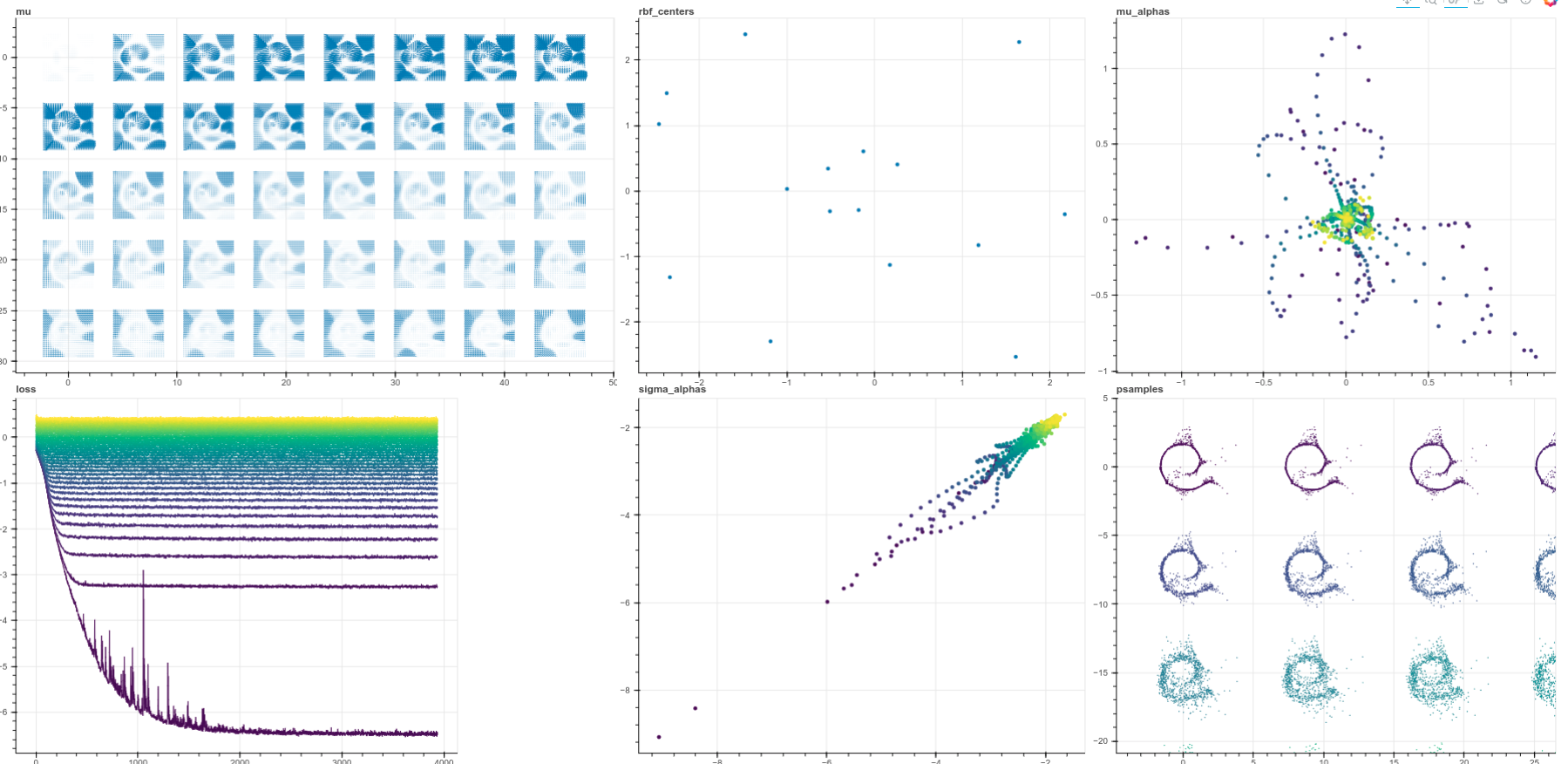
Here is a view of the full training dashboard, using the settings:
python swissroll.py --batch_size 100 --sample_size 10 --lr 0.007
In plots mu_alphas, loss, and
sigma_alphas, purple represents t=0, while yellow is t=40. The individual loss
curves are