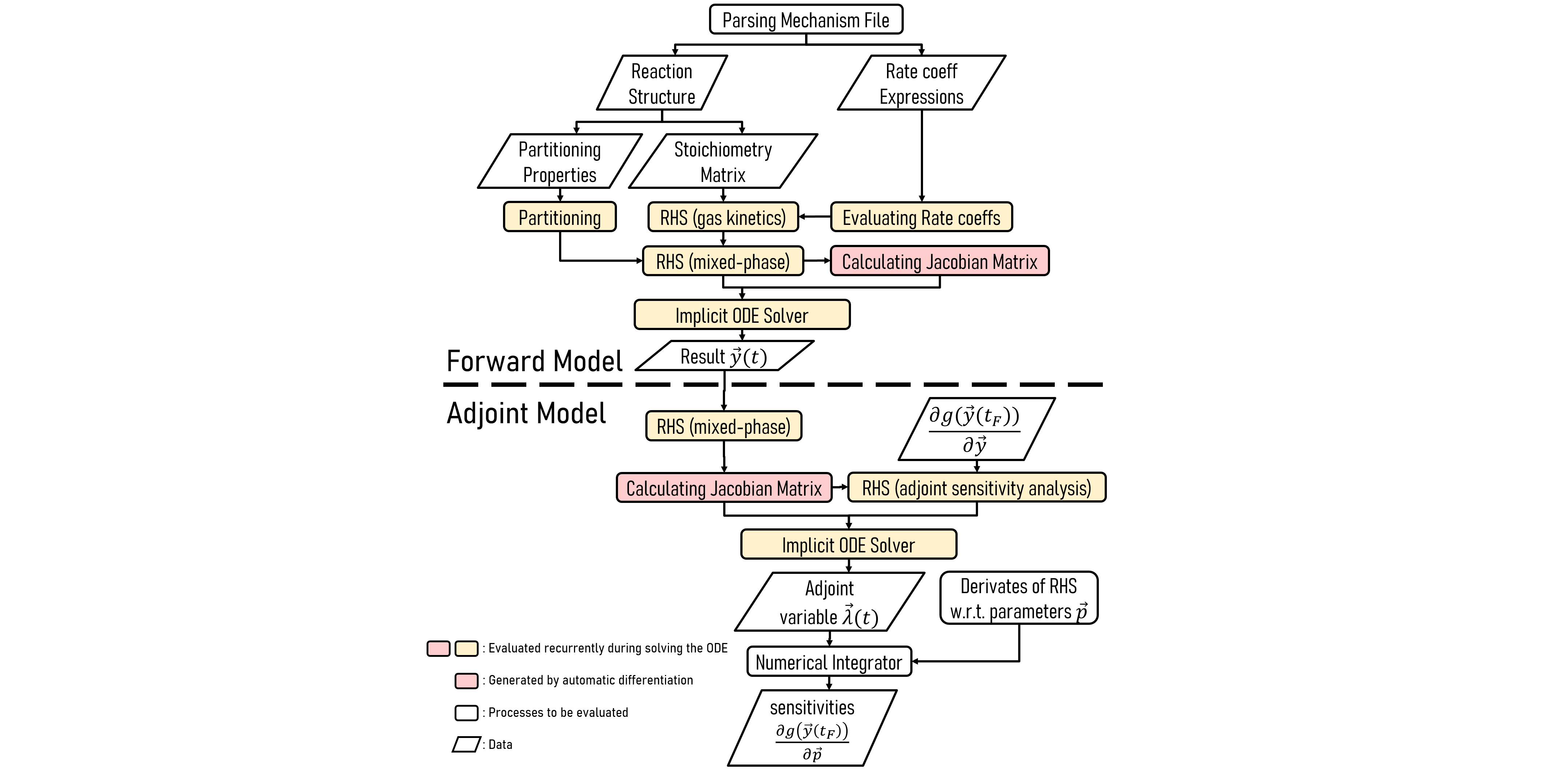
The JlBox is a julia package that simulates the evolution of chemicals in the atmosphere using
box model where advection effect is ignored. It is heavily inspired by Dr. David Topping's PyBox
and the two models could produce identical results, but JlBox is ~10x faster
than PyBox. It could handle full MCM mechanism (>10k eqns, 5k species) for both gas and mixed phase simulation.
This package works on Julia v1.5 .
Click this button to try JlBox on Binder:
In the root directory, execute docker build . -t jlbox to build a docker image
for jlbox, and then
docker run --rm -p 8888:8888 jlbox jupyter lab example/Demo.ipynb --ip=0.0.0.0 --no-browser
to open a jupyter notebook with examples of JlBox in it.
Work on Windows, MacOS and Linux.
- Open julia console, type
]to enter Package management state. - type
dev https://github.com/huanglangwen/JlBoxto download the JlBox. - type
build JlBoxto build JlBox. - type
test JlBoxto test its functionality. - Exit julia and
cdinto theJlBoxpackage folder (normally in.julia/dev/JlBox). - Run the example using
include("example/Simulation_*.jl")in julia console.
The JlBox package exposes functions like run_simulation and
run_simulation_aerosol_adjoint. There are three simulation types: gas only
simulation (only gas kinetics process) by passing GasConfig to
run_simulation, gas-aerosol simulation (gas kinetics+gas-aerosol partitioning)
by passing AerosolConfig to run_simulation and adjoint sensitivity analysis for the gas-aerosol
simulation. Users could tweak some parameters by changing the Config object as is illustrated in the examples.
Compared to PyBox, more optimizations are (going to be) added:
- constant folding for rate_values()
- caching rate_values, loss_gain matrix when solving ODE
- jacobian for gas kinetic (analytical)
- jacobian for partitioning process (fine grained AD)
- adjoint sensitivity analysis
- native ode solvers (TRBDF2)
- sparse iterative solver (CVODE_BDF with FGMRES)
- preconditioner (ILU & Tribanded)
- matrix free operator
- forward sensitivity analysis
- parallel linear solver (for native ODE solver only)
- parallel version of rate_values, loss_gain and jacobian
There are two stiff solvers that are practical for solving this model: CVODE_BDF from Sundials.jl and TRBDF2 from OrdinaryDiffEq.jl. Users have to carefully choose linear solvers used by them to achieve optimal performance.
- Dense direct linear solver: with
sparseturned off inSolverConfigCVODE_BDF(linear_solver=:Dense): single threadTRBDF2(linsolve=LinSolveFactorize())linsolvedoc: multi-threadusing CuArrays; TRBDF2(linsolve=LinSolveGPUFactorize()): GPU parallelized
- Sparse direct linear solver: (not recommended) with
sparseturned on inSolverConfigCVODE_BDF(linear_solver=:KLU)TRBDF2(linsolve=LinSolveFactorize())- Pardiso-MKL (in development)
- Sparse iterative linear solver: with
sparseturned on inSolverConfigCVODE_BDF(linear_solver=:FGMRES,prec=...,psetup=...,prec_side=2,krylov_dim=...): FGMRES with right side preconditioner, krylov_dim is suggested to be 0.1*num_states:FGMREScould be replaced with:GMRESor:BCGfor non-flexible GMRES or Bi-Conjugate Gradient Stabilized method but (maybe) with inferior performance.TRBDF2(linsolve=LinSolveGMRES()): (not recommended) hard to update preconditioners during simulation
For medium to large simulations (num_states >= 500), iterative methods (currently only FGMRES in CVODE_BDF is available) generally outperform direct methods. So for mixed phase simulations, we suggest to use iterative methods with ILU for initial preconditioning and LU of Tridiagonal for following preconditioning. For gas only simulations, direct solvers (default in CVODE_BDF and TRBDF2) usually run faster on small mechanisms like alpha-pinene mechanism.
The diff_method in SolverConfig are eventually passed to
select_jacobian(diff_method, ...) to select the intended jacobian for stiff
ODE solvers. default_psetup(diff_method1, diff_method2, krylov_dim) use the
same procedure to determine which jacobian to use when updating preconditioners.
We suggest to use accurate jacobian including coarse/fine-seeding,
fine_analytical for better performance except the second diff_method in psetup
where Tridiagonal preconditioner is less sensitive to the accuracy of jacobian.
However, it is recommended to use "fine_seeding" in adjoint sensitive analysis
as the result depends on the accuracy of Jacobian (explicitly included).
- "coarse_seeding":
aerosol_jac_coarse_seeding!naiive implementation of automatic differentiation of RHS function, the correctness and accuracy is guaranteed natually but memory use and performance is not optimal. - "fine_seeding":
aerosol_jac_fine_seeding!carefully crafted implementation only use automatic differentiation in subblocks. It produces identical results as the coarse one, but has better performance and uses less memory. - "fine_analytical":
aerosol_jac_fine_analytical!implementation of analytical solution of Jacobian. It is power and memory efficient. Its accuracy is not highly guaranteed but the number of convergence is similar to those with automatic difference. - "coarse_analytical":
aerosol_jac_coarse_analytical!highly simplified version of analytical solution. It is NOT accurate, only suitable for preconditioners. - "finite": finite differencing of RHS using FiniteDiff.jl. Slow, not very accurate, just for comparison.
- "gas_v" and "fine_seeding_v": Matrix-free operator version of the respective jacobian. Not recommended, as CVODE itself could approximate such operator using finite differencing.
There's only one option for gas phase jacobian: gas_jac! and all
methods except "finite" one calls gas_jac! for analytical solution in gas-only
block.
- lower tolerance of accuracy gives higher performance
- check accuracy of Jacobian (finitediff vs autodiff vs analytical)
- Note that coarse_seeding and fine_seeding has the same accuracy, but fine_seeding consumes less memory, while coarse_analytical is a very rough (and fast) estimation of fine_analytical, the latter is supposed to be accurate.
- or switch to ODE solvers that are less sensitive to the accuracy of Jacobian
- Low sensitivity: CVODE_BDF, TRBDF2, ABDF
- Medium sensitivity: KenCarp4, Rosenbrock23 and other Rosenbrock-W methods
- High sensitivity: Rodas and other Rosenbrock methods
- use parallel linear solvers
- like default linearsolvers in OrdinaryDiffEq.jl (LinSolveFactorize())
- or utilise GPU: LinSolveGPUFactorize()
- or use iterative sparse linear solvers (introduced previously)
- use higher krylov dimension when using iterative solvers (~0.1*num_states,num_states <= num_species*(1+num_bin))
- use better Preconditioner, but currently ILU and LU of Tridiagonal is generally good
- Modify the shape of state vector
y. - Modify
dydt!function adding new processes that effect the derivative ofy. - Choose a suitable way to make a new Jacobian function for the
dydt!: handwritten analytical function (has the highest potential for optimization but is error prone), generated auto differentiation or finite differentiation. These approaches can be mixed together like inaerosol_jac_seeding!where the analytical Jacobian is used for gas kinetics part. Sometimes it is hard to write an accurate (or correct) analytical Jacobian function while generated Jacobian is at least correct and accurate (AD is more accurate than FD). An accurate Jacobian matrix can significantly reduce the iteration steps of implicit ODE solvers. - Now you can run the model (remember to
using Reviseat the begining to avoid recompiling of the package everytime you change it). - With the Jacobian function, you could get adjoint sensitivity analysis out of box!