hurtstotouchfire/machine_learning_linear_models

A demo showcasing linear regression, reduced-rank regression and a linear system identification algorithm for modelling time series -- and when to apply them.

Machine Learning with Linear Models - a demo

Python 2.7 and 3+ compatible.

Table of Contents

• Description
• Usage

Description

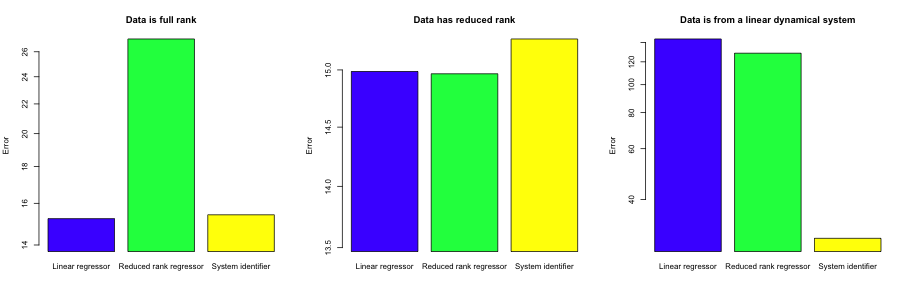
This small demo showcases a few simple but different linear models for mapping vectors of observations X to vectors of outcomes Y. Different assumptions about the data can lead to different levels of performance due to bias error – sometimes drastically.

For instance, when the mapping from X to Y is low rank (i.e., an information ‘bottleneck’), a technique called reduced rank regression (reduced_rank_regressor.py) can outperform standard multivariate linear regression (multivariate_regressor.py). When the mapping from X to Y is time dependent and based on an underlying linear dynamical system, applying a system identification technique (system_identifier.py) can result in big gains over both.

My Ph.D. supervisor Dr. Michael Bowling introduced me to RRR; Dr. Tijl De Bie gave a great talk on subspace system identification in 2005 that I modeled my implementation on: http://videolectures.net/slsfs05_bie_slasi/

Usage

Run the demo with:

python demo.py

You should see some output resembling the following:

Full rank data
  Multivariate Linear Regression
    Training error: 15.04019
    Testing error: 15.2303               <- best!
  Reduced Rank Regressor (rank = 10)
    Training error: 26.93426
    Testing error: 27.08937
  Linear Dynamical System
    Training error: 15.1246
    Testing error: 15.42221
Low rank data
  Multivariate Linear Regression
    Training error: 14.92995
    Testing error: 14.98602
  Reduced Rank Regressor (rank = 10)
    Training error: 14.95641
    Testing error: 14.96577              <- best!
  Linear Dynamical System
    Training error: 15.13557
    Testing error: 15.27782
Linear system data
  Multivariate Linear Regression
    Training error: 109.64736
    Testing error: 114.02463
  Reduced Rank Regressor (rank = 10)
    Training error: 124.58642
    Testing error: 128.55485
  Linear Dynamical System
    Training error: 28.49161
    Testing error: 29.33846              <- best!