tsmoothie

A python library for time-series smoothing and outlier detection in a vectorized way.

Overview

tsmoothie computes, in a fast and efficient way, the smoothing of single or multiple time-series.

The smoothing techniques available are:

Exponential Smoothing
Convolutional Smoothing with various window types (constant, hanning, hamming, bartlett, blackman)
Spectral Smoothing with Fourier Transform
Polynomial Smoothing
Spline Smoothing of various kind (linear, cubic, natural cubic)
Gaussian Smoothing
Binner Smoothing
LOWESS
Seasonal Decompose Smoothing of various kind (convolution, lowess, natural cubic spline)
Kalman Smoothing with customizable components (level, trend, seasonality, long seasonality)

tsmoothie provides the calculation of intervals as result of the smoothing process. This can be useful to identify outliers and anomalies in time-series.

In relation to the smoothing method used, the interval types available are:

sigma intervals
confidence intervals
predictions intervals
kalman intervals

tsmoothie can carry out a sliding smoothing approach to simulate an online usage. This is possible splitting the time-series into equal sized pieces and smoothing them independently. As always, this functionality is implemented in a vectorized way through the WindowWrapper class.

tsmoothie can operate time-series bootstrap through the BootstrappingWrapper class.

The supported bootstrap algorithms are:

none overlapping block bootstrap
moving block bootstrap
circular block bootstrap
stationary bootstrap

Media

Blog Posts:

Installation

pip install --upgrade tsmoothie

The module depends only on NumPy, SciPy and simdkalman. Python 3.6 or above is supported.

Usage: smoothing

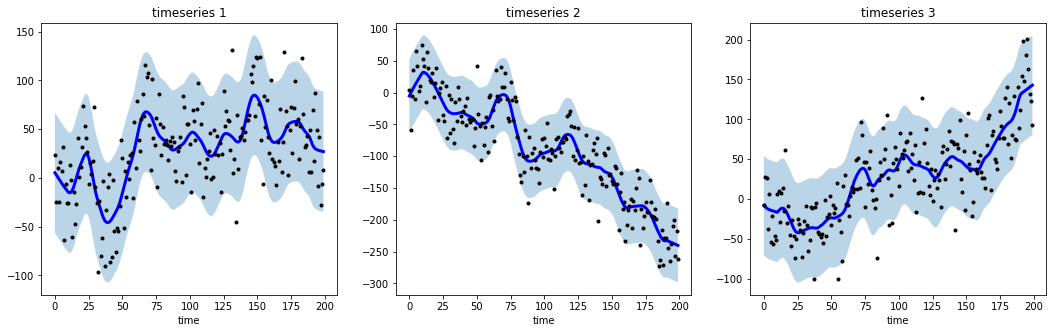
Below a couple of examples of how tsmoothie works. Full examples are available in the notebooks folder.

# import libraries
import numpy as np
import matplotlib.pyplot as plt
from tsmoothie.utils_func import sim_randomwalk
from tsmoothie.smoother import LowessSmoother

# generate 3 randomwalks of lenght 200
np.random.seed(123)
data = sim_randomwalk(n_series=3, timesteps=200, 
                      process_noise=10, measure_noise=30)

# operate smoothing
smoother = LowessSmoother(smooth_fraction=0.1, iterations=1)
smoother.smooth(data)

# generate intervals
low, up = smoother.get_intervals('prediction_interval')

# plot the smoothed timeseries with intervals
plt.figure(figsize=(18,5))

for i in range(3):
    
    plt.subplot(1,3,i+1)
    plt.plot(smoother.smooth_data[i], linewidth=3, color='blue')
    plt.plot(smoother.data[i], '.k')
    plt.title(f"timeseries {i+1}"); plt.xlabel('time')

    plt.fill_between(range(len(smoother.data[i])), low[i], up[i], alpha=0.3)

# import libraries
import numpy as np
import matplotlib.pyplot as plt
from tsmoothie.utils_func import sim_seasonal_data
from tsmoothie.smoother import DecomposeSmoother

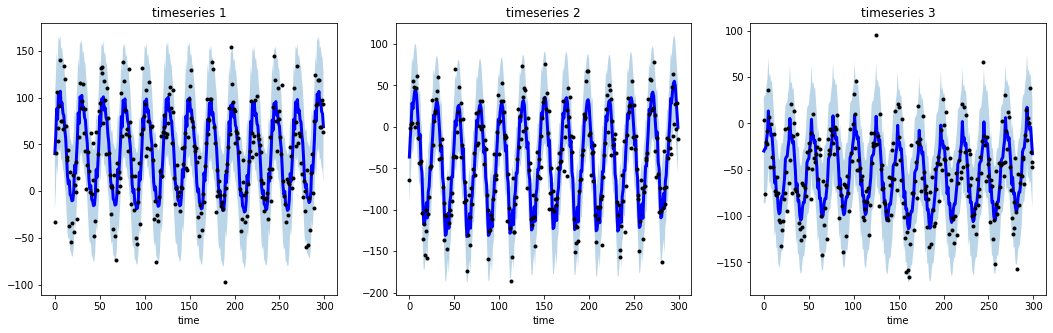
# generate 3 periodic timeseries of lenght 300
np.random.seed(123)
data = sim_seasonal_data(n_series=3, timesteps=300, 
                         freq=24, measure_noise=30)

# operate smoothing
smoother = DecomposeSmoother(smooth_type='lowess', periods=24,
                             smooth_fraction=0.3)
smoother.smooth(data)

# generate intervals
low, up = smoother.get_intervals('sigma_interval')

# plot the smoothed timeseries with intervals
plt.figure(figsize=(18,5))

for i in range(3):
    
    plt.subplot(1,3,i+1)
    plt.plot(smoother.smooth_data[i], linewidth=3, color='blue')
    plt.plot(smoother.data[i], '.k')
    plt.title(f"timeseries {i+1}"); plt.xlabel('time')

    plt.fill_between(range(len(smoother.data[i])), low[i], up[i], alpha=0.3)

All the available smoothers are fully integrable with sklearn (see here).

Usage: bootstrap

# import libraries
import numpy as np
import matplotlib.pyplot as plt
from tsmoothie.utils_func import sim_seasonal_data
from tsmoothie.smoother import ConvolutionSmoother
from tsmoothie.bootstrap import BootstrappingWrapper

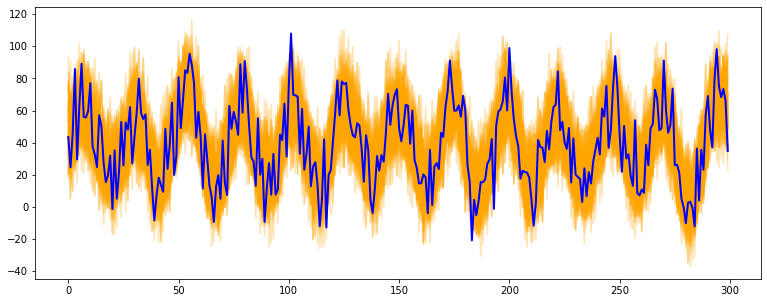
# generate a periodic timeseries of lenght 300
np.random.seed(123)
data = sim_seasonal_data(n_series=1, timesteps=300, 
                         freq=24, measure_noise=15)

# operate bootstrap
bts = BootstrappingWrapper(ConvolutionSmoother(window_len=8, window_type='ones'), 
                           bootstrap_type='mbb', block_length=24)
bts_samples = bts.sample(data, n_samples=100)

# plot the bootstrapped timeseries
plt.figure(figsize=(13,5))
plt.plot(bts_samples.T, alpha=0.3, c='orange')
plt.plot(data[0], c='blue', linewidth=2)

References

Polynomial, Spline, Gaussian and Binner smoothing are carried out building a regression on custom basis expansions. These implementations are based on the amazing intuitions of Matthew Drury available here
Time Series Modelling with Unobserved Components, Matteo M. Pelagatti
Bootstrap Methods in Time Series Analysis, Fanny Bergström, Stockholms universitet