A library for stochastic delay differential equations implementing published numerical schemes, utilities for constructing network models and handling simulation results, as well as bindings for MATLAB, Python. Our intent is to make it possible to use and benchmark available schemes on your favorite model, not invent new numerical schemes, so we have attempted to follow published results, documenting caveats, assumptions etc. Care will be taken to handle calculation of partial erivatives, to enable higher order schemes, optimization and inversion techniques.
The current focus is nailing down 'software carpentry' aspects of building a scientific library, and only preliminary sets of mathematical components are implemented, not for use pending v0.1 release, though I have stopped ruthless rebasing of master so it's safe to fork.
Currently the documentation, tests and benchmark are the best places to look to understand what you can do with SDDEKit.
Python, MATLAB bindings and C++ header are in the works, on separate
(ctype/cython/py-c-api, matlab, cpp respectively) branches of
this repo.
You can build the tests and benchmark if you have GCC (or a C99 compiler) and Make:
$ make tests
...
$ make bench_net_exc
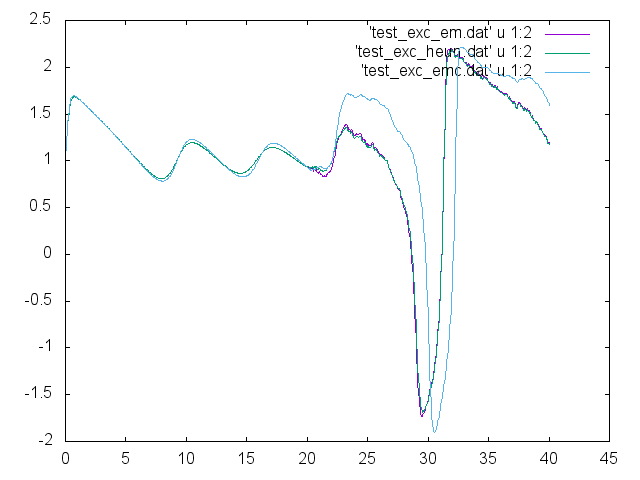
...Running the tests will generate some data files from one of the tests, which
tests different integration schemes on the same system. These can be compared with
the gnuplot script fig/exc_em_emcolor_heun.gpi
$ gnuplot fig/exc_em_emcolor_heun.gpiwhich produces
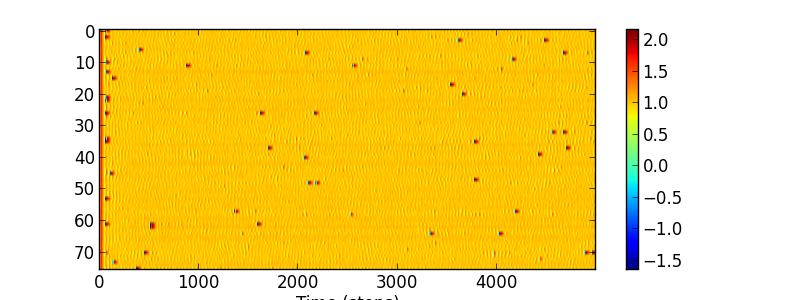
Running the benchmark will produce a trace bench_net_exc.dat which can be visualized
with fig/bench_net_exc.py, producing
As stated, these are in place to help build up the library at this point. In the future extensive examples for different kinds of systems & networks will be provided.
Because SDDEKit is a C library, it's straighforward to build it as a JavaScript library and embed it in HTML with Emscripten. With the benchmark mentioned above as an example, compile it natively,
$ make BUILD=fast -B -j bench_net_exc
...
$ ./bench_net_exc
[bench_net_exc] nnz=1560
[INFO] bench/bench_net_exc.c:71 (main) continuation required 23.766 sA little slow on this 2009 Core 2 Duo laptop. Now, with the Emscripten SDK installed, build an HTML page that runs the benchmark in your browser:
$ make CC=emcc BUILD=js OBJEXT=bc EXE=.html -B -j bench_net_exc.html
...Open bench_net_exc.html
with your browser. On this same machine, Safari
runs the benchmark in 74 s, Firefox 55 s.
Obviously for high-performance computing & science JS isn't ideal, but it could be useful for creating interactive graphics exploring dynamical systems.
Fork the code, try it out. See our documented issues or add your own.
Please follow the generic GitHub workflow:
- fork the repo
- create a topic branch, e.g add-foo-implementation
- make modifications
- git commit -m 'useful comments'
- push branch to your fork on GitHub
- open pull request
Here's way more detail w/ pictures
The current work on Python wrapper in the ctype branch follows the naming conventions
of the C library for the moment, drastically reducing the code required to use it. Though
if time permits, the API could be Python-ized.
To keep things general, most high-level components are exposed as interfaces through structs whose fields are just function pointers.
Contributing an implementation of a particular interface therefore implies
- writing implementations for each of the members of the interface struct
- writing a constructor function which
- alloc with sd_malloc
- fill out interface struct
- return it
- document & test
Keep in mind that if you 'subclass' an existing interface, some methods like
free should be available (and correctly implemented) in both
- Kloeden & Platen 1999 Numerical Solution of Stochastic Differential Equations.
- Fox et al 1998
- Mannella 200?
- Jimenez et al 2015
- Kuechler & Platen 2000