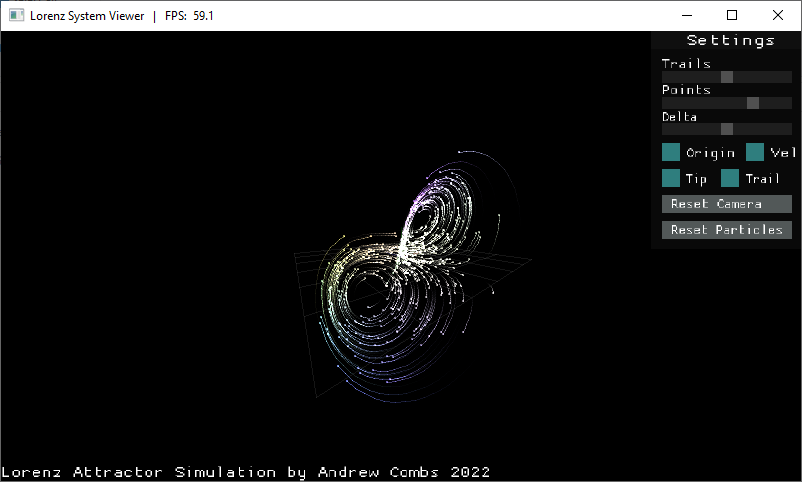
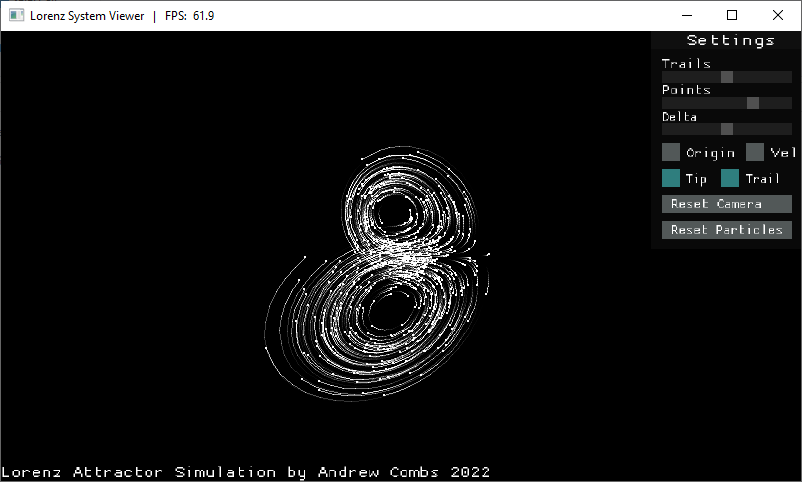
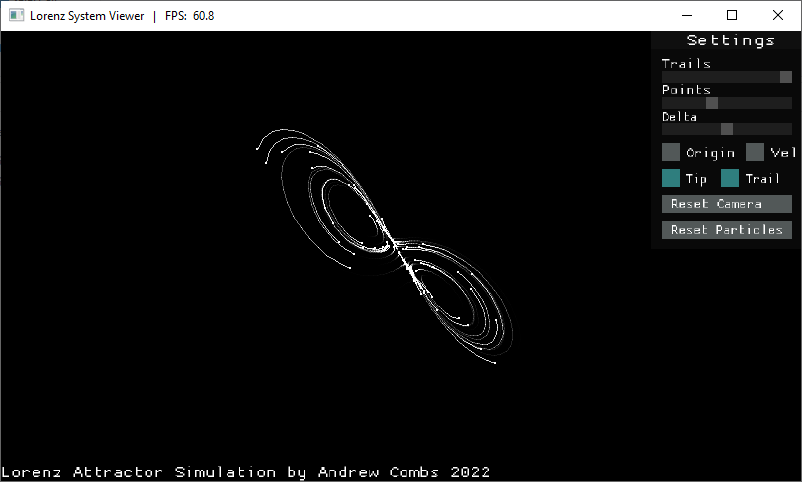
The Lorenz Attractor is a set of ordinary differential equations which approximate fluid convection. It's the most famous example of a set of attractors called strange attractors, which have chaotic or fractal structures. The exact equations and parameters used in the classic Lorenz attractor are as follows:
This project is an implementation of the Lorenz system using C and SDL2.0. Outside of SDL, SDL_ttf, and the standard C libraries, nothing else is used. The simulation shows how points with extremely close starting conditions (in this case within 0.01 units of each other) devolve into completely different paths over time.
This implementation includes the following user features:
- Orbiting camera
- GUI for controlling the simulation
- Point and path rendering
- Velocity rendering
In addition, the technical features include but are not limited to the following
- Custom 3D engine backend
- Custom GUI engine
- Fourth order Runge-Kutta ODE solver
While an accurate and visually nice simulation, there certainly are some drawbacks. Because of the CPU-bound nature, the maximum particles is limited to 1500 and the maximum length of the trails is 50. Additionally, setting the max number of points or max trail length too high will now allow the program to start (it will build, however running the program will yield nothing). Using the GPU for rendering and computing would likely solve these problems, and in the future I plan to remake this project using GPU acceleration.
Building this project should be fairly easy. After cloning the project, edit the Makefile and set SDL_INC, SDL_LNK, TTF_INC, and TTF_LNK to the respective include and link folders for SDL2.0 and SDL_ttf. If you're not using MinGW 32-bit, you'll also have to go through and change -lmingw32 and gcc to your compilers specification. To do a normal build, run make; this will make an executable called output.exe which has no optimizations. To do an optimized build, run make build; this will make an executable called build.exe which enables the -O3 and -Wall flag for all files.