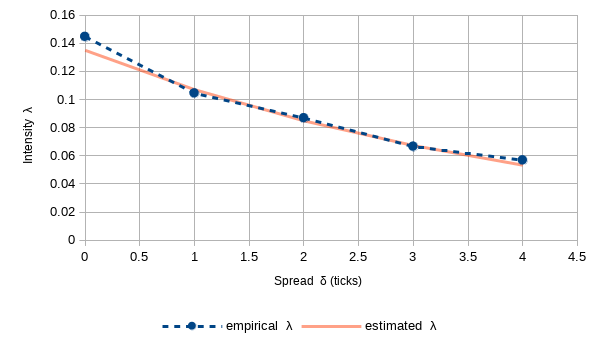
Poisson intensity of limit order execution, calibration of parameters A and k using level 1 tick data
A limit order placed at a price St ± δ, has the instantaneous probability of execution λ(δ)dt where the intensity λ(δ) is given by:
λ(δ) = A e -kδ
λ - Poisson order execution intensity
δ - spread (distance from mid price St)
A - parameter, positively related to trading intensity
k - parameter, positively related to market depth
Package Execution Intensity Estimator (EIE) contains single and multi threaded calibration procedure of A and k parameters.
Methods that calculate intensity λ(δ, A, k) and spread δ(λ, A, k) are provided as well.
Algorithm operates on level 1 tick data, therefore it is suitable in a setting where liquidity is not fully observable (i.e. dark pools).
Calibration is two step procedure performed separately for buy and sell limit orders.
Steps:
- For each spread δk of N predefined spreads (δ0 , δ1 , δ2 , ... δN-1) estimate execution intensity λ(δk) using "waiting time" approach described in [1] 4.4.2.. Result of this step is set of N points (δk , λ(δk)) on empirical Spread Intensity Curve (SIC)
- Estimate A and k based on N points from previous step. This can be achieved by various approaches.
Code implements two approaches described in [2] 3.2:
- LOG_REGRESSION performs OLS regression of log(λk) on δk. Finally k = -slope and A = e intercept
- MULTI_CURVE from set of N points creates Ns = (N*(N-1))/2 unique pairs fo points ((δx , λx) , (δy , λy)).
For each set of points solves the following set of equations for A' and k' :
λx = A' e -k'δx
λy = A' e -k'δy
Final estimates are A = mean(A'1 , A'2 , ... A'Ns) and k = mean(k'1 , k'2 , ... k'Ns)
Once A and k are calibrated, depending on context of usage, user can specify:
- Configuration parameters
double spreadStep = 0.00001; // increment of spread, greater than or equal to tick size
int nSpreads = 10; // number of spread increments, greater than 2
long w = 3600000; // 60 min, width of estimators sliding window
long dt = 10000 // 10 seconds, time scaling
- Create an instance of AkSolverFactory and specify SolverType
- Create an instance of FillRateEstimator
AkSolverFactory sf = new AkSolverFactory(SolverType.MULTI_CURVE);
IntensityEstimator ie = new IntensityEstimator(spreadStep, nSpreads, w, dt, sf);
- Pass an instance of ExecutorService to EstimationExecutor. Ensure minimum number of 5 threads is available. This step is required only for multithreaded estimation.
EstimationExecutor.setExecutor(executorService);
- Pass data (bid, ask, timestamp) to the instance of FillRateEstimator with onTick/onTickAsync call
- Run parameter estimates with estimate/estimateAsync call
while(loop){
...
// pass tick data to estimator
Future<Boolean> tickResult = ie.onTickAsync(bid, ask, timeStamp);
...
if (tickResult.get()) { // check if estimator can be called
Future<IntensityInfo> result = ie.estimateAsync(timeStamp);
...
IntensityInfo intensityInfo =result.get();
...
- Returned IntensityInfo instance gives access to parameters A and k for both buy and sell orders. Intensities λ(δ) and Spreads δ(λ) are returned by corresponding public methods.
Note:
- More details on usage and configuration can be found in IntensityEstimatorTest and javadoc comments
- Detailed test output is saved to target/intensity-log/ folder
- Single threaded outperforms multithreaded execution when less complex configurations are used