/inpla0.02

(old version) Inpla: Interaction nets as a programming language

Primary LanguageYaccOtherNOASSERTION

Inpla: Interaction nets as a programming language

What is Inpla

Inpla is a multi-threaded parallel interpreter of interaction nets, by using gcc and the Posix-thread library.

This is an old version, so plase use the current veresion.

Feature of Version 0.02

This version 0.02 (last update 30 March 2016) has the following features:

  • It is the fastest interpreter of interaction nets so far.
  • The syntax is a subset of Inets-project notation.
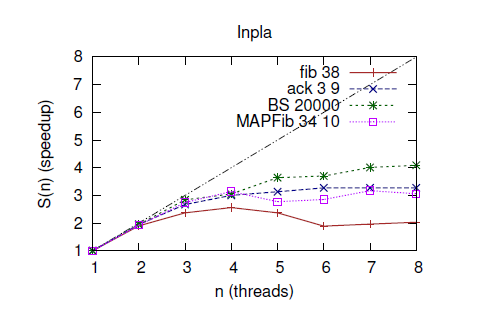
  • There are examples such that the multi-threaded Inpla runs faster than Standard ML and Python 2.7 on Core-i7 CPU and so on.
    • Execution time in second on interpreters (Linux PC, 2.4GHz, Core i7-3630QM, 16GB), where Inplan means that it was executed by using n threads.
SML Python Inpla Inpla1 Inpla2 Inpla3 Inpla4 Inpla5
fib 34 0.12 2.09 1.67 1.50 0.80 0.70 0.68 0.82
fib 38 0.66 16.32 11.39 10.22 5.68 4.47 4.40 4.75
ack 3 6 0.03 0.05 0.02 0.03 0.02 0.02 0.02 0.02
ack 3 9 0.06 - 0.69 0.72 0.38 0.27 0.24 0.24
bsort 10000 1.64 6.71 2.11 2.25 1.17 0.87 0.76 0.68
bsort 20000 8.38 30.35 8.38 8.93 4.57 3.64 2.98 2.49
MAPFib 34 5 0.49 9.89 8.92 8.09 4.55 3.21 2.54 2.73
MAPFib 34 10 0.94 19.77 17.81 17.23 9.28 6.44 5.22 5.38

speedup-ratio

Getting started

  • Requirement

    • gcc (>= 4.0), flex, bison

  • Build

    • Single-thread version: Use make command to build Inpla as follows (the symbol > means a shell prompt):
> make
  • Multi-thread version: Use make with thread option (it may also need make clear before that):
> make thread

Execution

Batch operation mode

  • Inpla starts in the batch operation mode that manages a file when an option -f is specified. For instance, the following command makes Inpla read a file sample/fib_9.in and execute it:
> ./inpla -f sample/fib_9.in
  • An option -t can specify the number of threads in the thread pool, in the case of the multi-thread version. For instance, using -t 4, Inpla uses 4 threads:
> ./inpla -f sample/fib_9.in
  • There are other sample files in the sample directory.
    • Ackerman function A 3 5 on unary natural numbers.
> ./inpla -f sample/AckSZ-3_5.in
  • Ackerman function A 3 5 on integer numbers.
> ./inpla -f sample/ack_3_5.in
  • Fibonacci number of 9 on unary natural numbers.
> ./inpla -f sample/FibSZ_9.in
  • Fibonacci number of 9 on integer numbers.
> ./inpla -f sample/fib_9.in
  • Evaluation of a lambda term 245II in YALE encoding, where 2 4 5 mean church numbers of lambda terms respectively and I is a lambda term $\lambda x.x$.
> ./inpla -f sample/245II.in

> ./inpla -f sample/linear-systemT.in
  • Bubble sort for a list that has 100 integer numbers as elements, at the best case, the worst case and the case of elements selected at random.
> ./inpla -f sample/bsort100.in
  • Insertion sort.
> ./inpla -f sample/isort100.in
  • Quick sort.
> ./inpla -f sample/qsort100.in
  • Merge sort.
> ./inpla -f sample/msort100.in
  • Map operation.
> ./inpla -f mapfib_34_5.in

Interactive mode

  • Inpla starts in the interactive mode as follows when it is invoked without the -f option:
> ./inpla
------------------------------------------------------------
      Inpla: Interaction nets as a programming language
                     version  0.02 [built: 16 Feb. 2016]
------------------------------------------------------------
$

  • The symbol $ is a prompt of this system.

  • The multi-thread version has an option -t in order to specify the number of threads in a thread pool. For instance, by using an option -t 4 Inpla starts with four threads in the pool:

> ./inpla -t 4
  • To quit this system, use exit command:
$ exit;

Options

  • Other options can be shown with -h option:
> ./inpla -h
Usage: inpla [options]

Options:
 -f <filename>    set input file name          (Defalut is    STDIN)
 -c <number>      set the size of term cells   (Defalut is   100000)
 -x <number>      set the size of the AP stack (Default is    10000)
 -t <number>      set the number of threads    (Default is        1)
 -h               print this help message

(The option -t is available when Inpla is compiled as the multi-thread version by using the command make thread.)

Introduction (how to use)

Inpla evaluates nets, which are built by connections between terms. First, we learn about terms and connections.

Terms

Terms are built by names and agents as follows:

<term> ::= <name>
         | <agentID>
         | <agentID> '(' <term> ',' ... ',' <term> ')'

  • Name: a string started with a small letter is regarded as a name in Inpla. For instance, x and y are identified as names.

  • Agent: a string started with a capital letter is identified as an agent in Inpla. For instance, A and Succ(x) are identified as agents.

Connections

A connections between two terms is expresssed by using the symbol ~, like x~A. Inpla evaluates connections. For instance, the x~A is evaluated such that the A is connected from the x:

$ x~A;

To show the connected terms from the name x, type just x:

$ x;
A

To dispose anything connceted from the x, use free command:

$ free x;
$ x;
<NON-DEFINED>

Many connections are also evaluated. For instance, x~A, x~y is evaluated as y~A (note that the x is disposed):

$ x~A, x~y;
$ y;
A
$ x;
<NON-DEFINED>
$ free y;
$ y;
<NON-DEFINED>

Interaction rules

Inpla rewrites connections between agents, according to interaction rules:

  • Interaction rules are defined as the following syntax:
<interaction rule> ::= <agent> `><` <agent> `=>` <connections> `;`

where

  • these <agent> must have only names as arguments, and each of the names must occur once in the <connections>.

  • Example 1: Incrementor on unary natural numbers

$ Inc(r) >< Z => r~S(Z);
$ Inc(r) >< S(x) => r~S(S(x));
$ Inc(result)~S(S(Z));
$ result;
S(S(S(Z))

To show the result as a natural number, use prnat command:

$ prnat result;
3
$ free result;
  • Example 2: Addition on unary natural numbers:
$ Add(x,r) >< Z => x~r;
$ Add(x,r) >< S(y) => Add(S(x),r)~y;
$ Add(S(Z), result)~S(S(Z));
$ result;
S(S(S(Z)))
$ prnat result;
3
$ free result;

Integer numbers

As an extension of Inpla, agents can have integer numbers as arguments. These are called attributes. For instance, A(100) is interpreted as an agent A that holds an attribute of the integer number 100:

$ x~A(100);
$ x;
A(100);
$ free x;

Built-in agents

Inpla has built-in agents:

  • Tuple0, Tuple1(x), Tuple2(x,y),...
    are written as
    (), (x), (x,y),...

  • Nil, Cons(x,xs)
    are written as
    [] and [x|xs], respectively.

  • A nested Cons that terminated at Nil is written as a list notation using brackets [ and ].

    • For instance,
      [x1 | [x2 | [ x3 | NIL]]]
      is written as
      [x1,x2,x3] .

The following is an example of built-in agents:

$ x~(100);
$ x;
(100)
$ free x;
$ x~[1,2,3];
$ x;
[1,2,3]
$ free x;

Attritubes are not agents, and thus the following raises an error:

$ x~100;
ERROR: The integer 100 is used as an agent.

Arithmetic expressions on attributes

Attiributes can be given as the results of arithmetic operation using where statement after connections:

<connections with expressions> ::= <connections> 
                       | <connections> 'where' <let-clause>* ';'
<let-clause> ::= <name> '=' <arithmetic expression>
  • For instance, the following is an expression using where:
$ x~(a) where b=3+5 a=b+10;
$ x;
(18);
$ free x;

Interaction rules with expressions on attributes

Attiributes can be managed by using a modifier int.

  • Example 1: Incrementor on an attribute:
$ Inc(r) >< (int a) => r~(b) where b=a+1;
$ Inc(result)~(10);
$ result;
(11)
$ free result;
  • Example 2: Addition operation on attributes:
$ Add(n2,r) >< (int i) => Add2(i, r)~n2;
$ Add2(int i, r) >< (int j) => r~(a) where a=i+j;
$ Add((10),r)~(3);
$ r;
(13)
$ free r;

Interaction rules with conditions on attributes

  • Conditional rewritings on attributes in interaction rules can be performed. The following is a general form:
<rule with conditions> ::= <agent> '><' <agent>
                          '|' <condition> '=>' <connections with expressions>
                          '|' <condition> '=>' <connections with expressions>
                              ...  
                          '|' '_'  '=>' <connections with expressions> ';'
  • For instance, the following shows rules to obtain a list that contains only even numbers:
// EvenList ------------------------------------------
EvenList(r) >< [] => r~[];
EvenList(r) >< [int x| xs]
| x%2==0 => r~[x | r1], EvenList(r1)~xs
| _      => EvenList(r)~xs;
// ---------------------------------------------------

$ EvenList(r)~[1,3,7,5,3,4,9,10];
$ r;
[4,10]
$ free r;
  • As another example Fibonacci number is taken:
// Fibonacci number ------------------------------------------
Fib(r) >< (int a)
| a == 0 => r~(0)
| a == 1 => r~(1)
| _ => Fib(n1)~(b), Fib(n2)~(c), Add(n2,r)~n1 
  where b=a-1 c=a-2; 

Add(n2,r) >< (int i)
=> Add2(i, r)~n2;

Add2(int i, r) >< (int j)
=> r~(a) where a=i+j;
// -----------------------------------------------------------

$ Fib(r)~(39);
$ r;
(63245986)
$ free r;

Commands

  • Inpla has the following commands:

    • free <name>;
      Terms connected from the <name> and itself are disposed.
    • <name>;
      Put a term connected from the <name>.
    • prnat <name>;
      Put a term connected from the <name> as a natural number.
    • use "filename";
      Read the filename in the current directory.
    • interface;
      Put all names that live.
    • exit;
      Quit the system.

  • Inpla has the following macro:

    • const <agent>=<int literal>;
      The <agent> is replaced with the <int literal>.

Publications

Related works

Licence

Copyright (c) 2016 Shinya SATO
Released under the MIT license
http://opensource.org/licenses/mit-license.php